Введение. Пастеризация является одним из самых распространенный процесс теплового воздействия на молоко. Пастеризация заключается в нагревании молока до заданной в соответствии с технологическим процессом температуры и выдержке при данной температуре некоторое время.
Принципиально важно с заданной точностью поддерживать температуру в технологическом оборудовании. Вызвано это тем, что при термической обработке изменяет вкусовые качества и аромат молока. Подвергнувшиеся температурному воздействию некоторые элементы, содержащиеся в молоке, изменяют свои физико-химические свойства, и соответственно меняется состав продукта. Нарушение температурного режима может привести к снижению качества молока и к появлению брака.
В связи с этим возникает необходимость в построении системы управления установкой, предназначенной для тепловой обработки молока с целью производства сыров, творога, кисломолочных продуктов, питьевого молока с заданными качественными показателями при различных условиях реальной работы. Поставленную задачу решим с применением положений теории систем с распределенными параметрами.
Создание математической модели. В качестве примера рассмотрим установку, представленную на рис. 1.

Рис. 1. Установка для пастеризации молока
Универсальный танк состоит из внутреннего вертикального цилиндрического резервуара, изготовленного из кислостойкой нержавеющей стали и заключенного в двустенный наружный корпус [1].
Местенное пространство между молочным резервуаром и корпусом служит водяной рубашкой. Горячая вода через стенку молочного резервуара нагревает молоко. Между корпусом и внешней обшивкой имеется воздушная прослойка, которая выполняет роль термоизоляции.
Математическую модель будем разрабатывать с применением уравнений теплопроводности [2]. Ниже представлен фрагмент математической модели.
Уравнение, описывающее тепловые процессы молока:
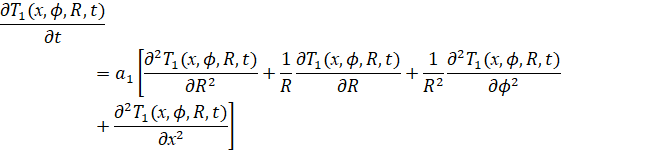 (1)
(1)
х0 ≤ x ≤ L1; R0 ≤ R ≤ R1; φ0 ≤ φ ≤ 3600
Уравнение 2 описывает тепловые процессы в молочном корпусе.
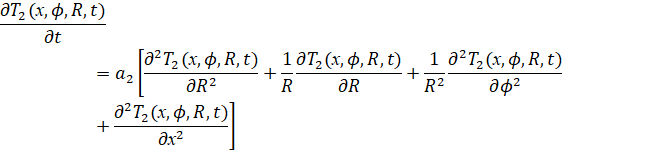 (2)
(2)
1) х0 ≤ x ≤ L2; R1 ≤ R ≤ R2; φ0 ≤ φ ≤ 3600
2) L1 ≤ x ≤ L2; R0 ≤ R ≤ R1; φ0 ≤ φ ≤ 3600
Уравнение 3 описывает тепловые процессы в водяной рубашкой.
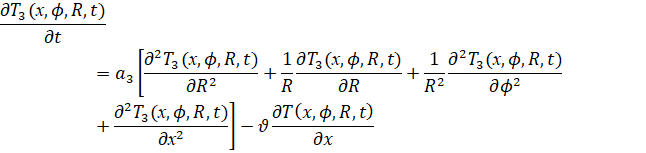 (3)
(3)
1) х0 ≤ x ≤ L3; R2 ≤ R ≤ R3; φ0 ≤ φ ≤ 3600
2) L2 ≤ x ≤ L3; R0 ≤ R ≤ R1; φ0 ≤ φ ≤ 3600
Уравнение 4 описывает тепловые процессы во внешней обшивке.
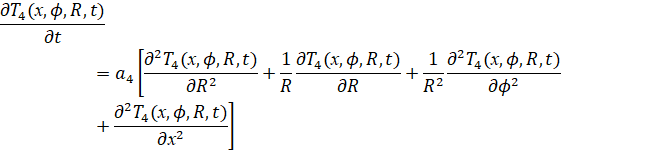 (4)
(4)
1) х0 ≤ x ≤ L4; R3 ≤ R ≤ R4; φ0 ≤ φ ≤ 3600
2) L3 ≤ x ≤ L4; R0 ≤ R ≤ R1; φ0 ≤ φ ≤ 3600
Считаем аппарат теплоизолированным с боковых сторон, таким образом, что тепловым воздействием извне можно пренебречь.
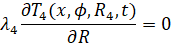 (5)
(5)
Запишем остальные граничные условия.
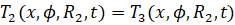 (6)
(6)
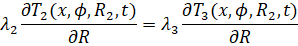 (7)
(7)
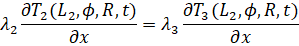 (8)
(8)
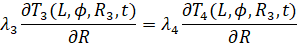 (9)
(9)
Для решения математической модели был выбран метод «сеток». С применением данного метода была составлена дискретная модель.
Решение полученной математической модели позволило построить графики переходного процесса в контрольных точках.
Для построения частотных характеристик аппроксимируем передаточные функции объекта, по каждой моде входного воздействия как апериодическое звено с чистым запаздыванием [5].
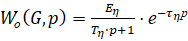 (10)
(10)
Искомая передаточная функция объекта по первой моде входного воздействия будет иметь вид:
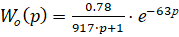 (11)
(11)
Для реализации управления был выбран распределенный высокоточный регулятор [4].
Передаточная функция рассчитываемого распределенного регулятора, согласно [4], имеет вид:
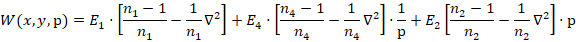
Для расчета настроек воспользуемся методикой изложенной в [3]. Запишем передаточную функцию полученного распределенного высокоточного регулятора:
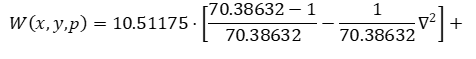
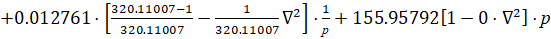 (12)
(12)
В результате моделирования получим переходные характеристики для заданных контрольных точек (рис. 2).
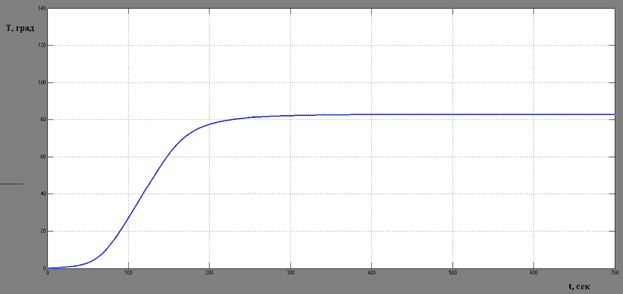
Рис. 2. График переходного процесса для одной из контрольных точек
Результаты моделирования свидетельствуют о том, что полученные настройки распределенного регулятора обеспечивают заданный процесс и необходимое время регулирования.
Заключение. В данной работе был рассмотрен вопрос автоматизации процесса пастеризации молока. Задачи, сформулированные для достижения поставленной цели, были решены в полном объеме.
Данные, полученные в результате моделирования, идентичны параметрам, полученным на реальном оборудовании. Данный факт позволяет утверждать об адекватности разработанной математической модели. Таким образом, полученная модель может быть использована для проведения дальнейших исследований. С её помощью был рассчитаны настройки распределенного регулятора.
Моделирование производилось с применением Delphi 7 и MATLAB Simulink. Результаты моделирования показали, что разработанная система полностью удовлетворяет поставленным требованиям.

.png&w=640&q=75)