Первые предпосылки нейросетей появились в середине XX века. Их развитие и внедрение в существующие технологии демонстрирует нарастающее число публикаций. На данный момент с помощью нейросетей можно решать различные задачи классификации, распознавания и прогнозирования.
В последние месяцы научным прорывом послужил искусственный интеллект от DeepMind, который решил научную проблему, над которой учёные бились полвека – за пару дней алгоритм впервые позволил спрогнозировать сворачивание белка с точностью до атома. Решение проблемы имело ключевое значение для понимания биологических основ жизни, и разработчики уже назвали это знаменательным моментом для всей отрасли - ИИ наконец-то становятся достаточно развитыми, чтобы решать действительно сложные научные проблемы [1].
В транспортной отрасли существует множество ежесуточно повторяемых вычислительных задач оперативного планирования, которые необходимо решать с помощью высококвалифицированных сотрудников. Такие операции необходимо автоматизировать с целью снижения трудоемкости.
Для решения задачи автоматизации работы логиста авторами разработан специализированный нейро-классификатор, выполняющий оперативный расчет необходимого количества вагонов (или контейнеров) с грузами разной объемной массы, допускаемых к совместной перевозке, учетом ограничений по вместимости и грузоподъемности подвижного состава.
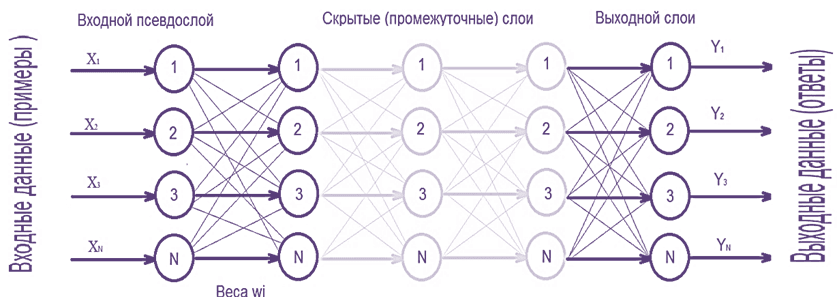
Рис. Схема используемой нейронной сети общем виде
Используемые входные данные при загрузке одним типоразмером груза (примеры для обучения нейросети):
- длина грузового места, м
- высота грузового места, м
- ширина грузового места, м
- объем одного грузового места, м3
- вес грузового места, кг
- общее количество груза, т
- объем груза, м3
- удельная масса, т/м3
- число мест в контейнере по массе и по объему
- тип контейнера (в данном случае 20' dv)
- длина, м
- высота, м
- ширина, м
- максимальная норма загрузки, кг
Раздельная загрузка грузами разной объемной массы составляет 16 вагонов. Рассмотрим решение задачи оптимальной загрузки сборного вагона. Математическую модель задачи запишем в стандартной форме задач линейного программирования – системы однородных уравнений и неравенств. Для формализованной записи математической модели введем следующие обозначения.
F – скалярная целевая функция;
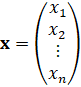– переменные задачи линейного программирования;
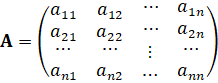– матрица условий (постоянных технологических или экономических параметров задачи);
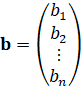– вектор ограничений (постоянных ограниченных ресурсов задачи);
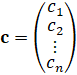– вектор показателей качества (весов переменных в целевой функции задачи).
В принятых обозначениях матричная форма записи задачи линейного программирования формулируется следующим образом.
Для известных матриц постоянных параметров задачи А, b и c требуется найти минимальное значение целевой функции:
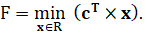(1)
При ограничениях:
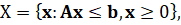(2)
где X – множество допустимых решений задачи.
Здесь предполагается совместимость размерностей А, x, b и c. Например, если в А – (m×n)-матрица, то х – n-мерный вектор-столбец, b – m-мерный вектор-столбец, cT – n-мерный вектор-строка.
Точное аналитическое решение системы уравнений находится методом псевдообратной матрицы [2]. Для рассмотренного выше примера, матрица условий А равна:
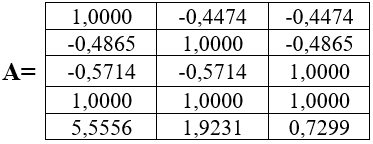
Вектор ограничений b равен:
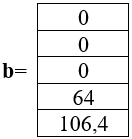
Оптимальное решение находится по формуле:
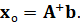(3)
где
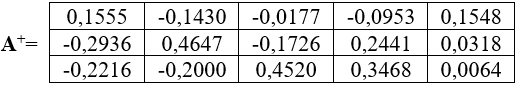
Решая уравнение (3), вычислим оптимальное значение вектора xо:
Полученные значения xо заносятся в таблицу.
Таблица
Расчет совместной загрузки вагона разными грузами
|
Расчетная масса груза |
Масса грузового места |
Расчетное число мест |
Округленное число мест |
Объем грузового места |
Масса груза в вагоне |
Объем груза в вагоне |
|---|---|---|---|---|---|---|
|
xi т |
Pi т |
шт |
шт |
м3 |
т |
м3 |
|
10,374 |
0,43 |
24,126 |
24,000 |
2,37 |
10,32 |
56,88 |
|
19,010 |
0,62 |
30,662 |
30,000 |
1,18 |
18,60 |
35,4 |
|
22,881 |
0,78 |
29,335 |
29,000 |
0,57 |
22,62 |
16,53 |
|
52,265 |
51,54 |
108,81 |
По средней массе сборного груза в вагоне, рассчитывается число вагонов при совместной загрузке:
= 
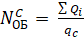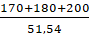=10,58 ≈11 вагонов
Таким образом, совместная загрузка грузов разных типоразмеров позволяет сократить необходимое число вагонов:
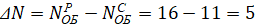вагонов.
Решение задачи сборной загрузки вагонов и контейнеров в общем случае для n типоразмеров грузов, допускаемых к совместной перевозке, требует значительных вычислительных затрат.
С целью автоматизации расчета числа необходимых вагонов или контейнеров при совместной загрузке грузами разных типоразмеров, был разработан специализированный нейровычислитель [3, 4].
В качестве входных данных в нейро-классификатор [4], необходимо подавать данные массива:
[120, 0.43, 165, 0.62, 278, 0.78]
где: 120, 165, 278 - общий вес груза (Qi, т)
0.43 , 0.62, 0.78 - масса грузового места (Pi , т)
Результатом работы искусственной нейро-сети служит выходной массив:
[57.657 9.5923]
где: 57.657 – суммарный вес груза в одном контейнере при оптимальной сборной загрузке в тоннах,
9.5923 – число сборных контейнеров.
Количество контейнеров (вагонов) округляется в большую сторону.
Заключение
В данной статье было проведено исследование возможности применения нейросетевых технологий в железнодорожной отрасли транспортной логистики. Результатом послужил высокоточный нейро-классификатор, использующийся для сборной загрузки контейнера. Технология сборной загрузки позволяет снизить количество используемых контейнеров, что косвенно влияет на себестоимость перевозки. Использование данной технологии позволяет минимизировать воздействие «человеческого фактора» и повышает точность оптимизации сборной загрузки вагонов и контейнеров.
