Повышение эффективности планетарных механизмов за счет использования корригированных зубчатых колес

Проектирование планетарных механизмов (только подбор числа зубьев колес, без расчета числа сателлитных блоков) по общепринятой методике требует выполнения 5 условий [1, 2].

1) главное условие синтеза, т.е. условие обеспечивающее получение заданного преобразования движения – это желательное условие, т.к. допускается отклонение передаточного числа 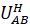 до ± 3%

2) условие соосности – это обязательное условие, т.к. его невыполнение может привести к резкому уменьшению КПД механизма или к заклиниванию колес или даже к невозможности сборки механизма зависит от схемы механизма)

Z₁-Z₂=Z₃+Z_2I (вид 2)

3) условие допустимости использования без подреза ножки зуба головкой режущего инструмента, т.н. нулевых колес колеса с коэффициентом смещения инструмента при нарезании колеса х = 0

Z_min≥15

4) ограничение на массу и размеры механизма – желательное условие, которое задается в виде верхней границы числа зубьев колес

Z_max≤100 – для зубчатых колес с зубьями снаружи (Zс),

Z_max≤150 – для зубчатых колес с зубьями внутри (Zв)

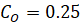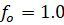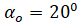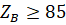
5) условие отсутствия интерференции зубьев для колес внутреннего зацепления (для колес, нарезанных стандартным инструментом – параметры инструментальной рейки – , , )   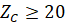ZB-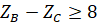 (это условие обеспечивает отсутствие всех видов интерференции).

Так как планетарный механизм имеет сложное конструктивное оформление, применение имеют только планетарные механизмы простой конструкции, которых всего 4 вида (рисунок).

Естественно, что чем меньше числа зубьев колес, тем меньше вес и размеры (габариты) механизма, поэтому надо стремиться к получению компактного и эффективного механизма. Существуют критерии оптимальности схемы планетарного механизма

• минимальность максимального радиального размера R_max,
• минимальность значения суммы чисел зубьев Σ_zi  планетарного механизма.

Число сателлитных блоков  К_С не должно быть кратным числу зубьев центральных колес механизма (колеса 1 и 3 на всех схемах).

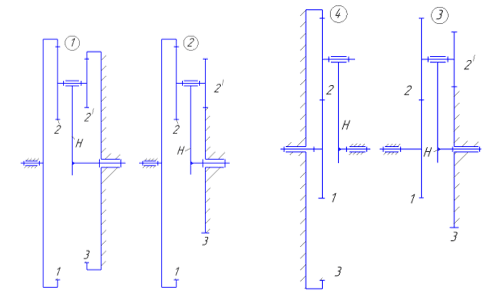
Рис. Типовые схемы планетарных зубчатых механизмов

Вышеуказанные условия ограничивают проектирование планетарного механизма только нулевыми колесами (Z_min≥17), которые удобны в изготовлении и сборке и легко и надежно обеспечивают выполнение обязательных условий соосности и отсутствия интерференции зубьев колес внутреннего зацепления. Авторы считают, что имеет интерес рассмотреть возможность использования корригированных колес, что хотя и усложнит процесс проектирования при соблюдении двух вышеуказанных условий, но и предоставит возможности получения компактного и легкого механизма (за счет уменьшения Z_min и значений Z_B, Z_C) при улучшении эффективности работы в целом. Известно, что корригированные колеса при выборе оптимальных коэффициентов смещения (таблицы, блокирующие контура) позволяют получить не только зубья без подреза ножки, но и получить дополнительно высокие качественные показатели зубчатого зацепления (плавность работы, уменьшение шума, уменьшения удельных скольжений и т.д.). От коэффициентов смещения х зависят коэффициент перекрытия (плавность и равномерность движения), толщина зубьев у основания и вершин зуба (прочность на изгиб), радиусы кривизны рабочих участков профиля зубьев, отсутствие подрезания ножки зуба головкой режущего инструмента, т.е. то, что определяет общую прочность зуба. Выбором сочетаний x₁ и x₂ можно влиять на скорость скольжения профилей зубьев друг по другу и соответственно на коэффициент удельного скольжения, т.е. на факторы, определяющие износостойкость зубьев колеса.

1. Для схемы 3, где нет внутреннего зацепления, такой переход (от нулевых колес к корригированным) наиболее легок. Условие соосности имеет вид

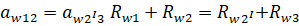
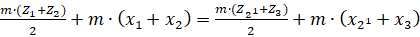  (1)

Задаваясь (скажем для конкретности) оптимальными коэффициентами x₁ и x₂ из таблиц или блокирующих контуров, значением х для меньшего из колес второй ступени (для конкретности x₂₁) из условия (1) получим значение x₃

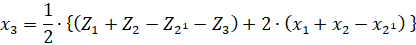
2. Остальные схемы должны подчиняться дополнительно условию интерференции зубьев колес внутреннего зацепления, которое для корригированных колес имеет более сложное выражение.

а) Интерференция рабочего участка одного зуба с нерабочим участком другого зуба

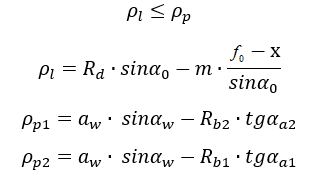
где ρ_l – радиус кривизны эвольвенты на основной окружности, ρ_p – радиус кривизны эвольвенты на нижнем краю активной части профиля зуба [3, 4].

б) Интерференция эвольвентной поверхности колеса 2 (с внутренними зубьями) с кромкой зуба шестерни 1 (с внешними зубьями)

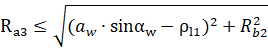
Компактность схемы планетарного механизма на основе корригированных зубчатых колес обеспечена уменьшением Z_min (выбирая коэффициент смещения при нарезании колеса по условию 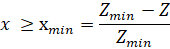 ) для условия (3), где мы можем для Z принимать любое значение допустимое по технологии изготовления зубчатых колес (например, Z_MIN≥ 11 при нарезании колес по методу обкатки), а также уменьшением значений Z_в, Z_с для условия (5).

Для планетарных механизмов существуют критерии оптимальности спроектированной схемы – максимальный радиальный размер (зависит от схемы механизма), сумма чисел зубьев всех колес механизма (без учета числа сателлитных блоков), число сателлитных блоков К_С не должно быть кратно числам зубьев центральных колес механизма.

Пример. Рассмотрим проектирование планетарного механизма вида 4 (имеет оба вида зацепления) для передаточного числа U_1H=54/11.

а) Расчет на основе нулевых колес (по существующей методике) дал следующие значения – числа зубьев колес Z₁=22, Z₂=32, Z₃=86, максимально допустимое число сателлитных блоков по условию соседства равно 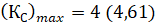, рабочее число сателлитных блоков по условию сборки равно К_С = 4 (при параметре сборки N = 0). Все указанные выше условия проектирования полностью выполняются.

Б) Расчет на основе корригированных зубчатых колес (предлагаемая методика) дал следующие значения. Z₁=11, Z₂=16, Z₃=43, 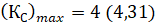, К_С = 3 (при параметре сборки N = 0). Для выбранных чисел зубьев колес выполняется условие отсутствия подреза ножки зуба – данных колес х_1min = 0,357, х_2min = 0,064.

Выполняются оба условия отсутствия интерференции зубьев:

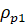 ^{= 2,292 ≥  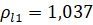и 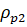 = 3,31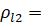7 ≥  1,507}

а также

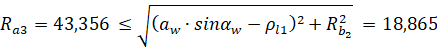  мм

Схема планетарного механизма на основе корригированных колес также более оптимальна – по радиальному размеру (Z₃=43 у корригированного механизма против Z₃=86 у механизма с нулевыми колесами), по сумме чисел зубьев колес механизма (70 против 140). У обоих механизмов рабочее число сателлитных блоков К_С не кратно числам зубьев центральных колес 1 и 3.

Выводы. Использование корригированных зубчатых колес вместо нулевых зубчатых колес при проектировании планетарных механизмов позволяет получить более компактный механизм при одновременном улучшении его качественных показателей. Это достигается при небольшом увеличении требований к качеству изготовления колес и степени точности сборки механизма. В итоге получается механизм более близкий к критериям оптимальности.