Контроль горного оборудования по низкочастотным вибрациям имеет ряд недостатков: невозможность обнаружения и идентификации многих видов дефектов, которые являются причиной отказов подшипников; сложность разделения составляющих вибрации; сложность обнаружения зарождающихся дефектов. Измерения параметров вибрации в широком частотном диапазоне не несут информации о процессах, происходящих в самом подшипнике.
Предпринятые нами попытки применения наиболее распространенных методов, (измерения СКЗ вибропараметров в широком диапазоне частот (от 10 до 1000 Гц), измерение пик-фактора и узкополосных спектров), не позволили с достаточной достоверностью выявлять неисправности подшипниковых узлов буровых станков на ранних стадиях развития и прогнозировать срок их безотказной работы [1, 2, 3, 4].
Поэтому в работе применен алгоритм обработки сигнала, учитывающий то, что вибрации, регистрируемые на корпусе подшипникового узла, представляют сложный колебательный процесс, который можно представить в виде:
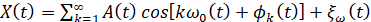. (1)
Он состоит из наложения на квазиполигармонический процесс - в области низких и средних частот, случайного широкополосного стационарного процесса ξω(t) – в области высоких частот.
При этом мы исходили из того, что информация о процессах, происходящих в самом подшипнике – ударные взаимодействия элементов подшипника, трение при проскальзывании тел качения, содержится в высокочастотной широкополосной случайной составляющей. Для выделения этой полезной информации и формирование диагностических признаков о зарождающихся дефектах в подшипнике, поступим следующим образом. Путем Фурье – преобразования получали спектральную плотность мощности этого сигнала:
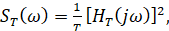
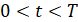, (2)
где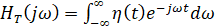 
частотное представление сигнала.
Выделим из этого сигнала фильтрацией выделялась узкополосная компонента ξΔt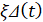
(в диапазоне шириной в 1/3 октавы) с наибольшей мощностью – эта область соответствует резонансным колебаниям наружного кольца подшипника:
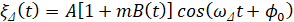, (3)
где 0<m<1 – глубина модуляции.
В свою очередь
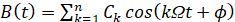, (4)
т.е. представляет амплитудно-модулированный процесс вида:
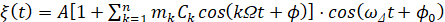, (5)
где mк – парциальный коэффициент модуляции; Ω - угловая частота модуляции.
Поэтому следующим шагом путем фильтрации выделяется медленно меняющийся колебательный процесс, т.е. получаем огибающую исходного высокочастотного сигнала. Затем, снова выполнив Фурье – преобразование, получим «спектр огибающей». Таким образом, оказалось возможным разделить в пространстве частотные составляющие, связанные с характерными дефектами подшипников.
Количественно техническое состояние с помощью спектра огибающей удобно оценивать с помощью обобщенного вибродиагностического параметра по формуле:
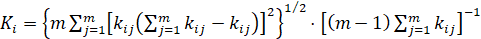. (6)
В этом случае в матрицу (6) следует подставлять значения парциальных коэффициентов модуляции для характерных частот, связанных с определенными видами дефектов.
Приведенная методика позволяет сопоставить и ранжировать по динамическим свойствам всю совокупность обследованных машин и выявить наиболее неблагополучные места, где вероятнее всего могут произойти повреждения.
Проводя периодические вибрационные измерения и наблюдая за изменением обобщенного вибродиагностического параметра K(t), строились трендовые характеристики, вид которых показан на рисунке.
Здесь в начальный период эксплуатации наблюдается медленное уменьшение величины К по мере изнашивания элементов подшипника и увеличения зазоров. В момент, соответствующий точке А, происходит резкое увеличение интенсивности изнашивания, вызываемого ударно-усталостными процессами вследствие превышения величиной зазора предельного значения.
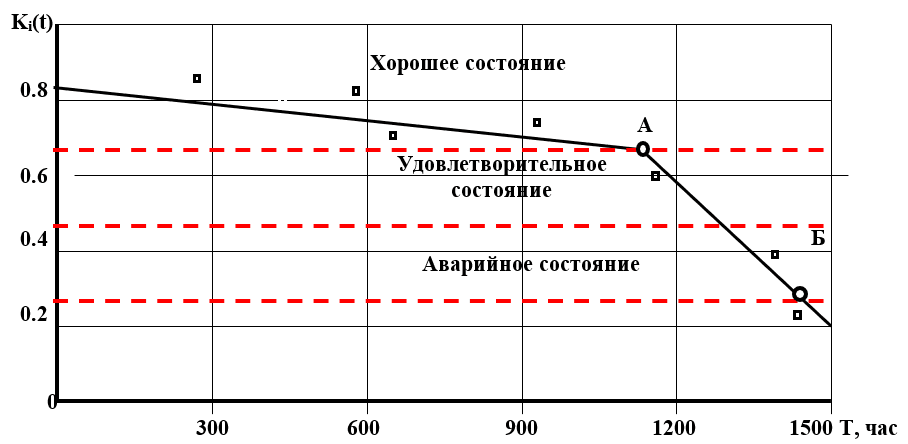
Рис. Зависимость обобщенного вибрационного параметра от времени
Принимая линейный закон для скорости убывания величины K(t):
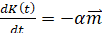, (7)
Используя известное из теории надежности соотношение между вероятностью безотказной работы подшипниковой опоры P(T) и интенсивностью отказов подшипника λ(T), можно записать:
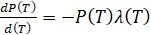или 
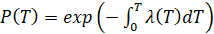. (8)
Принимая интенсивность отказов величиной постоянной и пропорциональной энергии колебательных процессов, происходящих в подшипнике при перекатывании тел качения, и проявляющихся в виде компонент с частотами, кратными kZω0, где Z – число тел качения; ω0 – частота вращения вала; k=1,2,3..... – номер гармоники:
λT=cDkZω0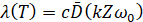
, (9)
где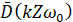 
– средние значение мощности колебаний на частотах, кратных частоте вращений; c – коэффициент пропорциональности. Тогда:
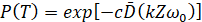. (10)
А среднее время наработки между отказами:
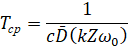(11)
Таким образом, зависимости (10) и (11) устанавливают взаимосвязь показателей надежности опорных узлов с параметрами их вибрационного состояния.
В результате выполненных исследований получены следующие выводы:
- в результате исследований обоснован мониторинг технического состояния опорных узлов горного оборудования, позволяющий определить и прогнозировать величину остаточного ресурса и уровень качества опорных узлов в заданные моменты времени;
- контроль и наблюдение за уровнем вибропараметров позволяет определить характер неисправностей в механических системах горного оборудования.
