Распространение расширенного метода комбинирования связей на неголономные системы

Рассматривается вопрос распространения расширенного метода комбинирования связей на неголономные системы с неидеальными связями. Получены дифференциальные уравнения движения механической системы, которые обладают тем свойством, что из этих уравнений можно получить явные выражения сил связей, не зависящие от сил трения.

Рассматривается механическая система из N материальных точек с массами 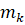 (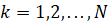), положение которых относительно инерциальной декартовой системы координат определяется радиус-векторами  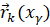 ( 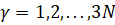). Система находится под действием заданных сил 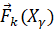и стеснена совместными и независимыми связями, среди которых имеются как геометрические

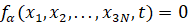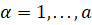  ( ),      (1)

так и кинематические, вообще говоря, нелинейные

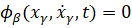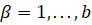   ( ).  (2)

Многообразия допустимых состояний системы представляется в виде:

x_γ=a_γ(q_i,t); x_γ=b_γ(q_i,p_j,t) , где q₁,q₂,...,q_n(n=3N-a) – обобщенные координаты; p_j  (j=1,2,...,r; r=3N-(a+b)) – независимые скоростные параметры.

Силу реакций 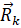 разложим на две составляющие: силу связей 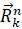и силу трения 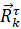, причем

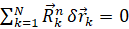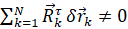;  (3)

и перемещение 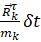 есть возможное перемещение. Эти силы имеют следующий вид:

,

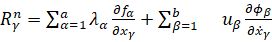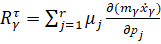.        (4)

где λ_α,u_β и μ_j – некоторые коэффициенты.

Показано, что если в какой-то момент времени известны положения и скорости точек системы, а также действующие на эти точки активные силы 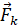, то силы связей  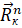определяются и будут одними и теми же, независимо от того, обладает ли данная система трением или нет.

В силу (3) общее уравнение динамики для рассматриваемых систем с неидеальными связями принимает следующий вид

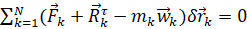.      (5)

Оно представляет собой необходимое и достаточное условие соответствия заданным силам совместимого со связями движения системы при известном законе трения системы.

Даётся обобщение принципа наименьшего принуждения Гаусса для неголономных систем с неидеальными связями (для систем с трением) в случае, когда возможные перемещения удовлетворяют условиям расширенного метода комбинирования связей. Согласно обобщенному принципу Гаусса, среди возможных ускорений действительные ускорения точек системы с неидеальными связями обращают в минимум функцию

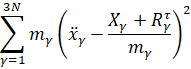  (6)

где 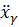– действительные ускорения точек системы. Этот принцип приводит к дифференциальным уравнениям действительного движения системы с неидеальными связями

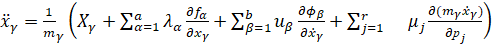.        (7)

Таким образом, в данной статье расширенный метод комбинирования связей распространен на неголономные системы с неидеальными связями. Показано, что для таких систем имеет место общее уравнение динамики, которое позволяет обобщить принцип наименьшего принуждения Гаусса.

В заключении приведены выводы и перечислены основные результаты:

1. Дано распространение расширенного метода комбинирования связей на неголономные системы с неидеальными связями. Показано, что для таких систем имеет место общее уравнение динамики.
2. Дано обобщение принципа наименьшего принуждения Гаусса для неголономных систем с неидеальными связями в рамках расширенного метода комбинирования связей.