Построение полиномов экстремальных степеней, действительные корни которых идентифицируются с помощью алгоритма сортировки

Введение и постановка вопроса. Задача нахождения корней полинома имеет содержательную математическую историю. Ее решение существенно для важных теоретических и прикладных применений. В частности, к нахождению всех корней характеристического полинома матрицы сводится проблема анализа устойчивости линейной системы обыкновенных дифференциальных уравнений [4, 3]. Анализ устойчивости линейной системы управления выполняется на основе нахождения корней характеристической функции, представляющей отношение полиномов [2]. Как собственные значения линейных операторов корни характеристических полиномов применяются для построения ортогонального базиса, разложение в котором используются при моделировании физических процессов в полупроводниках [1, 5].

В [7] излагается инвариантный метод программной идентификации действительных корней полиномов без указания области расположения корней. Метод основан на алгоритме устойчивой адресной сортировки с взаимно однозначным соответствием входных и выходных индексов. При этом минимально используются вычислительные операции, которые согласно алгоритму заменяются на операции сравнения значений модуля полинома и индексов его локализованных минимумов. В результате не накапливается погрешность, и все корни идентифицируются без потери значащих цифр в формате представления входных данных. При этом программно определяется область расположения корней полинома. В частности, так определяются корни полинома 26-й степени, среди них есть корни, которые взаимно отделены на 0.0001.

Возникает вопрос: каковы предельные возможности метода, какую максимальную степень может иметь полином, корни которого можно идентифицировать данным методом на основе сортировки?

Идентификация действительных корней полинома в заданной области полуоси. Для удобства изложения вначале используется простейшая сортировка со свойствами устойчивости и явного операторного выражения взаимно однозначного соответствия входных и выходных индексов сортируемых элементов. Она является частным случаем сортировки многопутевым слиянием на основе матриц сравнения, в то же время – это простая модификация сортировки подсчетом [8].  Пусть, например, требуется упорядочить по нестрогому возрастанию одномерный массив a=(8,4,-4,-3,15). Отсортированный массив обозначается с. Матрица сравнений МС приведена ниже:

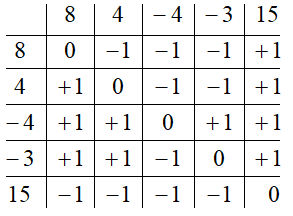
Номер j-го элемента входного массива a в отсортированном массиве с подсчитывается как число нулей и плюсов в j-м столбце МС над диагональю, включая диагональный элемент, сложенное с числом плюсов под диагональю (нумерация от j=1). В частности, a[1]=8→1+1+1+1+0=4→c[4],a[2]=4→0+1+0+1+1=3→c[3]. Аналогично, a3=-4→c1, a[4]=-3→c[2], a[5]=15→c[5]. Ядро процедуры (n=5), в дальнейшем sort00, сводится к циклическим операторам:

for j:=1 to n do

begin

k:= 0;

for i:=1 to j do

if a[j]>=a[i]  then k:=k+1;

for i:=j+1 to n do

if a[j]>a[i]  then k:=k+1;

           c[k]:=a[j]; e[k]:=j;

           end;

МС антисимметрична относительно главной диагонали, отсюда возможны четыре разновидности правила подсчета [6]. Сортировка устойчива. Операторы c[k]:=a[j]; e[k]:=j; в цикле for j:=1 to n do каждому входному индексу j сопоставляют единственный выходной индекс k, и обратно: e[k]:=j; Входные индексы на выходе сортировки располагаются в порядке отсортированных элементов.

Пусть n элементов входного массива

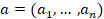         (1)

после сортировки принимают вид:

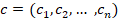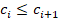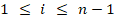, , .  (2)

Соответствие индексов из (1), (2) образует подстановку

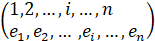      (3)

где нижний ряд задается массивом адресов

e=(e₁,e₂, … ,e_n),  (4)

образуемых операторами c[k]:=a[j]; e[k]:=j; при этом порядок индексов e_i совпадает с порядком отсортированных элементов c_i. Массив e определяет количество и положение локально экстремальных элементов массива a при произвольно заданном радиусе окрестности локализации ε₀, где ε₀ – натуральное число. Именно, локально минимальный элемент с индексом k, где 1 ≤ k ≤ n, массива a определяется тем, что

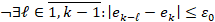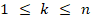,.     (5)

где e_k, e_k-l – индексы из (3), (4), расположенные в порядке отсортированных элементов (2). Соотношение (5) означает, что ни один из входных индексов отсортированных элементов, предшествующих элементу c_k, не может принадлежать окрестности радиуса ε₀ индекса e_k этого элемента во входном массиве. Иными словами, ни один из таких индексов не является индексом предшествующего элемента в отсортированном массиве, поэтому e_k – индекс наименьшего элемента в окрестности радиуса ε₀.Программная идентификация минимального элемента имеет вид (ε₀= eps0):

{sort00(n,a,c,e);} k:=1; while k<= n do

вegin for L:=1 to k-1  do if  abs(e[k]-e[k-L]) <= eps0 then goto 11; ik:= e[k];

11: k:= k+1 end;

В этом фрагменте ik – индекс идентифицированного локально минимального элемента. Минимальность понимается исключительно в смысле отношения порядка. Идентифицированный минимум может оказаться первым (наименьшим), максимум – последним (наибольшим) в цепочке равных элементов. В результате выполнения цикла по k локализуются одновременно все минимальные элементы последовательности в окрестности произвольно фиксированного радиуса ε₀ (eps0). Предложенная идентификация исключает накопление погрешности, поскольку не выполняет вычислений: она использует только сравнения элементов при сортировке и сравнение их индексов для локальной минимизации. В результате минимальные элементы идентифицируются с точностью до формата представления данных.

Для решения поставленной задачи описанная сортировка заменяется на существенно более быструю сортировку слиянием по матрицам сравнений, обладающую всеми изложенными качествами для идентификации корней. В приводимой ниже программе, полностью заимствованной из [7], она описывается как procedure sort(varnn0: longint; varc: vect1; vare: vect2); Для выполнения численного эксперимента корни в программе задаются в разделе констант массивом b. Ниже, в подпрограмме  function func (var x: extended): extended; они циклически собираются в полином степени n1=26 согласно основной теореме высшей алгебры из разложения

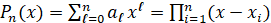.         (6)

programKORDEMINPOLsortnew;

{$APPTYPE CONSOLE}

uses

SysUtils;

label 21, 22; const n1=26;

b: array [1..n1] of extended =

(1, 2, 3, 4.0007, 4.0008, 5, 6.0001, 6.0002, 7, 8, 9, 10, 11, 12, 13,

14, 15, 16, 17, 18, 19.0003, 19.0002, 20, 21, 22, 23);

eps=1E-44; eps0=0.000049; h=eps0/33; n00=1512; mm=4; x00=-15; x11=70;

type vect1=array [0..4*n00] of extended; vect2=array [0..4*n00] of longint;

vec=array [0..n1] of extended;

var i,j,k,l,ee,nn0: longint; a,c: vect1; e: vect2; b1:vec;

aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1: extended;

functionfunc (var x: extended): extended;

var i1: 1..n1;p:extended;

begin p:=1; for i1:=1 to n1 do p:=p*(x-b1[i1]); func:=abs(p); end;

procedure min1 (var x: extended;var ee: longint);

begin min:=func(x); ee:=0; for i:=1 to mm do begin

x:=xk0+i*h0; if min >func(x) then begin min:=func(x); ee:=i; end; end; end;

procedure sort(var nn0: longint; var c: vect1; var e: vect2);

type vecc=array[0..4*n00] of longint;

var ab: integer;  i,j,k,l,m,r,nm,p,n: longint;  e1, e2: vecc;

begin

p := trunc(ln(nn0)/ln(2)); if p<> ln(nn0)/ln(2) then p := p+1;

n := round(exp(p*ln(2)));

for l := 1 to n do if l<=nn0 then e[l] := l else ab:=1;

for r := 1 to p do begin m :=round(exp(r*ln(2))); nm:=n div m;

for k := 0 to nm-1 do begin

for l := 1 to m div 2 do begin

if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab := l

else e1[l] := e[k * m + l];

if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab := 1

else e2[l] := e[k * m + m div 2 + l] end;

i := 1; j := 0; while i + j <= m do begin

ifi = m div 2 + 1 then ab := -1;

if j = m div 2 then ab := 1;

if (k * m + i> nn0) or (e[k * m + i]>nn0)

or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)

then ab:=1;

if (i<= m div 2) and (j <= m div 2 -1) and  (k * m + i<= nn0)

and (k * m + m div 2 + j <= nn0-1)

then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab := 1 else

begin if c[e2[j + 1]] - c[e1[i]]= 0 then ab := 0;

         if c[e2[j + 1]] - c[e1[i]]> 0 then ab := 1;

         if c[e2[j + 1]] - c[e1[i]]< 0 then ab := -1

end; if ab >= 0 then

begin  e[k * m + i + j] := e1[i]; i := i + 1  end

else begin  e[k * m + i + j] := e2[j + 1]; j := j + 1 end

end end end end;

begin

aaa:=1e62; nn0:=n00; hh:=nn0*h;

x0:=x00; for i:=1 to n1 do b1[i]:=b[i]; while x0 <= x11 do

begin for i:=1 to nn0 do begin  x:=x0+i*h; c[i]:=func(x); end;

sort(nn0, c, e); k:=1; while k<= nn0 do

begin for l := 1 to k-1 do if abs(e[k]-e[k-l]) <= eps0/h then goto 22; xk:= x0+e[k]*h;

eps1:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; h0:=abs(2*eps1)/mm;

while abs(eps1) > eps do begin x:=xk0; min1(x,ee); eps1:=eps1/1.2;

xk0:=xk0+ee*h0-eps1; xk1:=xk0+ee*h0+eps1; h0:=abs(2*eps1)/mm; end;

if func(xk)= 0 then begin x:=xk; goto 21; end; x:=xk0+ee*h0+eps1;

for i:= 1 to 2 do begin z:=x+i*h; if  func(x) >= func(z) then goto 22; end;

for i:= 1 to 2 do begin z1:=x-i*h; if  func(x) >= func(z1) then goto 22; end;

if abs(aaa-x)<=1e-20 then goto 22;

21: writeln ('  ', x,'  ',func(x)); aaa:=x;

22: k:=k+1 end; x0:=x0 + hh end;

readln;

end.

Результат работы программы состоит в вычислении всех 26 корней, среди идентифицированных есть корни, взаимно отделенные на 0.0001:

      4.000800000000000E+0000   0.00000000000000E+0000

      4.000700000000000E+0000   0.00000000000000E+0000

   …………………………………………………………..

      6.000100000000000E+0000   0.00000000000000E+0000

      6.000200000000000E+0000   0.00000000000000E+0000

   …………………………………………………………..

      1.900020000000000E+0001   0.00000000000000E+0000

      1.900030000000000E+0001   0.00000000000000E+0000

Поиск корней выполнялся на отрезке с границами x00=-15; x11=70; Тот же результат, но более медленно достигается, например, на отрезке x00=-70; x11=70; От известных методов предложенный отличается по построению, инвариантным условиям применения и минимизацией погрешности.

Повышение степени полинома и идентификация его корней. Если в программе KORDEMINPOLsortnew заменить подпрограмму-функцию

function func (var x: extended): extended;

var i1: 1..n1;p:extended;

  begin p:=1; for i1:=1 to n1 do p:=p*(x-b1[i1]); func:=abs(p); end;

на подпрограмму, в которой каждый сомножитель (x-b1[i1]) дополняется до разности квадратов (sqr(x)-sqr(b1[i1])), то степень полинома удвоится, и половина корней станут отрицательными. Соответственно, надлежит изменить область поиска корней на x00=-75; x11=75;

label 21, 22; const n1=26;

b: array [1..n1] of extended =

(1, 2, 3, 4.0007, 4.0008, 5, 6.0001, 6.0002, 7, 8, 9, 10, 11, 12, 13,

14, 15, 16, 17, 18, 19.0003, 19.0002, 20, 21, 22, 23);

eps=1E-44; eps0=0.000049; h=eps0/40; n00=1512; mm=4; x00=-75; x11=75;

type vect1=array [0..4*n00] of extended; vect2=array [0..4*n00] of longint;

vec=array [0..n1] of extended;

var i,j,k,l,ee,nn0: longint; a,c: vect1; e: vect2; b1:vec;

aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1: extended;

function func (var x: extended): extended;

var i1: 1..n1;p,p1: extended;

begin p:=1; for i1:=1 to n1 do p:=p*(sqr(x)-sqr(b1[i1])); func:=abs(p) end;

Результатом работы модифицированной программы станут все корни полинома 52-й степени, включая отделенные на 0.0001:

      -4.000800000000000E+0000   0.00000000000000E+0000

      -4.000700000000000E+0000   0.00000000000000E+0000

     ………………………………………………………………

      -6.000100000000000E+0000   0.00000000000000E+0000

      -6.000200000000000E+0000   0.00000000000000E+0000

    ………………………………………………………………

      -1.900020000000000E+0001   0.00000000000000E+0000

          -1.900030000000000E+0001   0.00000000000000E+0000

     ………………………………………………………………

      4.000800000000000E+0000   0.00000000000000E+0000

      4.000700000000000E+0000   0.00000000000000E+0000

      …………………………………………………………….

      6.000100000000000E+0000   0.00000000000000E+0000

      6.000200000000000E+0000   0.00000000000000E+0000

      …………………………………………………………….

      1.900020000000000E+0001   0.00000000000000E+0000

      1.900030000000000E+0001   0.00000000000000E+0000

Продолжая аналогичными приемами увеличивать степень полинома, можно прийти к подпрограмме-функции, которая задает корни полинома 226-й степени, все его корни действительны, различны, между ними есть взаимно отделенные на 0.0001:

label 21, 22; const n1=26;

b: array [1..n1] of extended =

(1, 2, 3, 4.0007, 4.0008, 5, 6.0001, 6.0002, 7, 8, 9, 10, 11, 12, 13,

14, 15, 16, 17, 18, 19.0003, 19.0002, 20, 21, 22, 23);

b0: array [1..n1] of extended =

(1.05, 2.05, 3.05, 4.0007+0.05, 4.0008+0.05, 5+0.05, 6.0001+0.05, 6.0002+0.05, 7+0.05,  

8+0.05,

9+0.05, 10+0.05, 11+0.05, 12+0.05, 13+0.05,

14+0.05, 15+0.05, 16+0.05, 17+0.05, 18+0.05, 19.0003+0.05, 19.0002+0.05, 20+0.05,

21+0.05, 22+0.05, 23+0.05);

b00: array [1..n1] of extended =

(1.055, 2.055, 3.055, 4.0007+0.055, 4.0008+0.055, 5+0.055, 6.0001+0.055, 6.0002+0.055,

7+0.055, 8+0.055,

9+0.055, 10+0.055, 11+0.055, 12+0.055, 13+0.055,

14+0.055, 15+0.055, 16+0.055, 17+0.055, 18+0.055,

19.0003+0.055, 19.0002+0.055, 20+0.055, 21+0.055, 22+0.055, 23+0.055);

b000: array [1..n1] of extended =

(1.055+0.5, 2.055+0.5, 3.055+0.5, 4.0007+0.055+0.5, 4.0008+0.055+0.5, 5+0.055+0.5,

6.0001+0.055+0.5,

6.0002+0.055+0.5, 7+0.055+0.5, 8+0.055+0.5,

9+0.055+0.5, 10+0.055+0.5, 11+0.055+0.5, 12+0.055+0.5, 13+0.055+0.5,

14+0.055+0.5, 15+0.055+0.5, 16+0.055+0.5, 17+0.055+0.5, 18+0.055+0.5,

19.0003+0.055+0.5, 19.0002+0.055+0.5, 20+0.055+0.5, 21+0.055+0.5, 22+0.055+0.5,

23+0.055+0.5);

eps=1E-44; eps0=0.000049; h=eps0/40; n00=1512; mm=4; x00=-35; x11=35;

type vect1=array [0..4*n00] of extended; vect2=array [0..4*n00] of longint;

vec=array [0..n1] of extended;

var i,j,k,l,ee,nn0: longint; a,c: vect1; e: vect2; b1:vec;

aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1: extended;

function func (var x: extended): extended;

var i1: 1..n1;p,p1,p0,p00,p000:extended;

begin p:=1; for i1:=1 to n1 do p:=p*(sqr(x)-sqr(b1[i1]));p0:=1; for i1:=1 to n1 do

p0:=p0*(sqr(x)-sqr(b0[i1]));

p00:=1; for i1:=1 to n1 do p00:=p00*(sqr(x)-sqr(b00[i1]));  p000:=1; for i1:=1 to n1 do

p000:=p000*(sqr(x)-sqr(b000[i1]));

p1:=(sqr(x)-sqr(0.1))*(sqr(x)-sqr(0.2))*(sqr(x)-sqr(0.3))*(sqr(x)-sqr(0.4))*(sqr(x)-

sqr(0.5))*(sqr(x)-sqr(0.6))*(sqr(x)-sqr(0.7))*(sqr(x)-sqr(0.8))*(sqr(x)-sqr(0.9));

func:=abs(p*p0*p1*p00*p000) end;

Иных изменений в приведенной выше программе KORDEMINPOLsortnew не вводится, за исключением того, что область поиска сужается: x00=-25; x11=25; Это сделано затем, чтобы не приходилось долго ждать результата работы программы (собственно программа инвариантна относительно длины промежутка поиска корней). С данными модификациями программа найдет все 226 действительных корней полинома 226-й степени:

  -2.35550000000000E+0001   0.00000000000000E+0000

  -2.30550000000000E+0001   0.00000000000000E+0000

  -2.30500000000000E+0001   0.00000000000000E+0000

  -2.30000000000000E+0001   0.00000000000000E+0000

   …………………………………………………………..

  -1.90002000000000E+0001   0.00000000000000E+0000

  -1.90003000000000E+0001   0.00000000000000E+0000

…………………………………………………………….

  -2.00000000000000E-0001   0.00000000000000E+0000

  -1.00000000000000E-0001   0.00000000000000E+0000

   1.00000000000000E-0001   0.00000000000000E+0000

   2.00000000000000E-0001   0.00000000000000E+0000

……………………………………………………………

   2.00000000000000E+0000   0.00000000000000E+0000

   2.05000000000000E+0000   0.00000000000000E+0000

   2.05500000000000E+0000   0.00000000000000E+0000

   2.55500000000000E+0000   0.00000000000000E+0000

   ………………………………………………………….

   1.90003000000000E+0001   0.00000000000000E+0000

   1.90002000000000E+0001   0.00000000000000E+0000

   1.90502000000000E+0001   0.00000000000000E+0000

   1.90503000000000E+0001   0.00000000000000E+0000

   1.90553000000000E+0001   0.00000000000000E+0000

   1.90552000000000E+0001   0.00000000000000E+0000

…………………………………………………………

   2.30000000000000E+0001   0.00000000000000E+0000

   2.30500000000000E+0001   0.00000000000000E+0000

   2.30550000000000E+0001   0.00000000000000E+0000

   2.35550000000000E+0001   0.00000000000000E+0000

Курсивом выделены корни, отличие между которыми составляет 0.0001. Все корни найдены без потери значащих цифр в формате представления числовых данных.

Заключение. Предложено построение программы идентификации действительных корней полиномов с возрастающей степенью. Программа построена на основе устойчивой адресной сортировки слиянием по матрицам сравнений с прямой и обратной адресацией к входным и выходным индексам сортируемых элементов. Вследствие минимального количества вычислительных операций программа не создает накопления погрешности. В ходе численного эксперимента были идентифицированы 226 действительных корней полинома 226-й степени, среди которых были корни взаимно различавшиеся на 0.0001. Корни идентифицированы без потери значащих цифр в формате представления данных. Тем самым проиллюстрированы возможности применения исследуемого метода в случае полиномов выше 200-й степени.