Введение. В настоящее время все большую популярность в среде анализа и работы с наборами данных завоевывают алгоритмы машинного обучения. Машинное обучение позволяет с высокой производительностью работать над распознаванием текста, классификации изображений, усовершенствовать различные интернет поисковики и переводчики. Глубокое обучение является одним из методов машинного обучения, который превосходит остальные методы, за счет большей производительности и лучшей точности при работе с большими объемами данных. Статья рассматривает на практике применение технологии глубокого обучения.
Исходные данные. В качестве dataset будет использоваться набор цифр языка жестов. В этой выборке находится более двух тысяч изображений языка жестов. В таком стиле общения используются цифры от нуля до девяти, т.е. используется десять уникальных знаков. Рисунок 1 демонстрирует знак единицы и нуля, индексы которых соответственно равны 260 и 900.

Рис. 1. Демонстрация dataset
Проблемой имеющегося dataset является наличие трехмерных изображений, в следствии чего необходимо сделать их двумерными [1]. В результате набор “x” содержит 410 изображений размером 64 на 64пикселей, а набор “y” содержит 410 меток, означающих ноль или один (рис.2).

Рис.2. Демонстрация подвыборки
Logistic Regression. Наиболее эффективным алгоритмом для так называемой двоичной классификации является логистическая регрессия [2]. На самом деле логистическая регрессия является типичным примером простой нейронной сети, в следствии чего на вход подаются изображения из dataset, а каждое изображение состоит из пикселей, в результате чего каждый пиксель должен иметь свой начальный вес. Тем самым вес каждого пикселя инициализируем как 0.01, а начальное смещение будет равно 0:
def initialize_weights_and_bias(dimension):
w = np.full((dimension,1),0.01)
b = 0.0
return w, b
После чего необходимо транспонировать входную матрицу и подать её в сигмовидную функцию, что вернуть вероятность попадания в тот или иной класс. Целесообразность применяемого метода можно проверить путем определения значения ошибки. Если подать изображение со знаком один и метку, равную единице в уравнение (1), то ошибка будет равна нулю, что означает о правильности использования выбранного алгоритма.
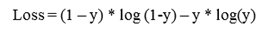 (1)
(1)
Однако в нашем алгоритме происходит не совсем точное прогнозирование из-за высокой так называемой стоимости, в следствии чего необходимо найти алгоритм, который будет заниматься изучением и правильным распределением весов и смещений, которые обеспечивают минимизацию функции затрат. Таким алгоритмов является алгоритм градиентного спуска [3].
Gradient Descent. Суть данного алгоритма заключается в минимизации функции затрат и нахождении производной функции потерь одного веса, найденного относительно всех весов. Наиболее распространенная функция потерь среднеквадратичной ошибки является:
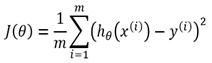 (2)
(2)
Производной этой функции по отношению к любому весу является:
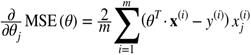 (3)
(3)
Применив этот алгоритм, была минимизирована функция затрат и можно перейти к обучению модели, а также анализу точности работы представленного алгоритма.
Обучение модели. После всех проделанных шагов необходимо произвести обучение модели с помощью метода логистической регрессии, задав начальные веса, равные 0.01 и количество итераций, равное 150. В результате получаем точность, равную 93 %, что является хорошим показателем, но всё же не достаточным. Такая логистическая регрессия считается искусственно-созданной, так как она применяется в виде написанной функции, поэтому точность является ниже. Если применить логистическую регрессию в виде модуля из библиотеки sklearn, то точность будет выше за счет использования дополнительных параметров оптимизации и регуляризации. В результате на рисунке 3 представлена удовлетворяющая точность.

Рис. 3. Результат работы логистической регрессии
Вывод. В статье рассмотрены методы анализа входных данных, описаны различия между машинным и глубоким обучением, а также приведена реализация примера использования одного из алгоритмов глубокого обучения, а именно логистической регрессии для классификации изображений, обозначающих изображения языка жестов. Представленный алгоритм показал высокую точность классификации, за счет предварительно использованного алгоритма минимизации функции затрат, а именно алгоритма градиентного спуска.

.png&w=640&q=75)