Актуальные вопросы математического моделирования

«Наука начинается там, где начинают измерять».
Д.И. Менделеев

Введение

Структурно работа состоит из двух частей. В первой части предложена и исследована модель замкнутого пространства. После чего, на основе вводимой модели пространства, рассмотрены процессы в различных областях знаний, вопросы в области электродинамики, физиологии, описываются сердечно-сосудистая система человека, процесс мышления.

В статье предложен принцип математического моделирования физиологических процессов. В качестве примера рассмотрена модель переключения внимания между внешними и внутренними объектами.

После чего показан принцип построения модели на примере системы кровообращения человека, описаны отдельные процессы электродинамики в контексте с предложенной моделью пространства.

Принцип моделирования – наложения структуры рассматриваемых процессов на элементы предложенной модели пространства.

Во второй части более детально описывается модель замкнутого пространства, определяется структура модели в целом, рассматриваются отдельные ее свойства.

Цель – выявить, показать и исследовать общие закономерности, которые присутствуют на первый взгляд в различных областях знаний, в частности закономерности, которые присутствуют в процессе мышления человека, процессе функционирования сердечно-сосудистой системы человека, а также в отдельных процессах электродинамики.

Материалы и методы исследования. За основу для нашего исследования, в качестве предлагаемой модели, взят фрагмент специально сконструированного геометрического пространства S, определена структура модели в целом, рассмотрены отдельные ее свойства. Основным методом исследования является наложение существенных компонентов рассматриваемых процессов на фрагменты пространства. Так же исследование производится посредством метода наблюдения.

Часть 1. Принципы построения математической модели

1.1. Модель геометрического пространства ее структура и свойства

Модель пространства, которая предлагается в качестве основы для анализа, структурно состоит из четырех основных элементов, это три плоскостные структуры α, β, γ и сферическая поверхность, которую мы обозначим как S_p.

Составные части вышеуказанных элементов модели, в зависимости от их местонахождения, условно делятся на положительные и отрицательные, северные и южные, восточные и западные.

В частности, в качестве основы для комплексного рассмотрения общих закономерностей процесса мышления нас интересуют элементы плоскостной структуры α.

Рассмотрим модель пространства в горизонтальной плоскости α, где определена криволинейная сеть, состоящая из семейства прямых и окружностей [19, с. 2].

Области на плоскости α будут направлены в соответствии с направленностью прямых и дуг, которые на них находятся (рис. 1).

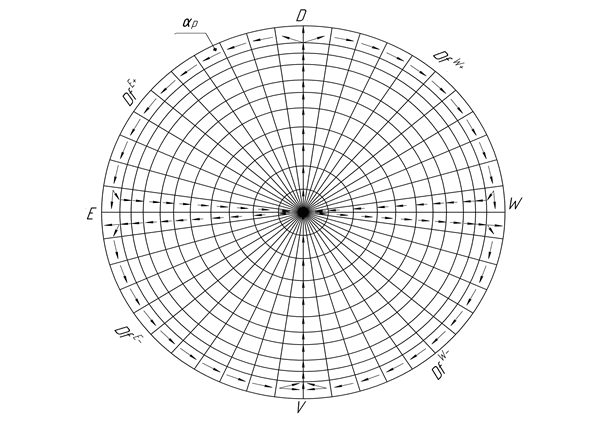
Рис. 1. Модель геометрического пространства в горизонтальной плоскости

В соответствии с направленностью областей заключим в них числовые ряды от 1 до 9, числовые ряды будут заключены в интервале между особыми или назовем их критическими точками [11] (D, V, E, W, O). В области, которым принадлежат критические точки, заключим число 0.

Направленность таких рядов будет согласована с направленностью областей, в которых они расположены (рис.2).

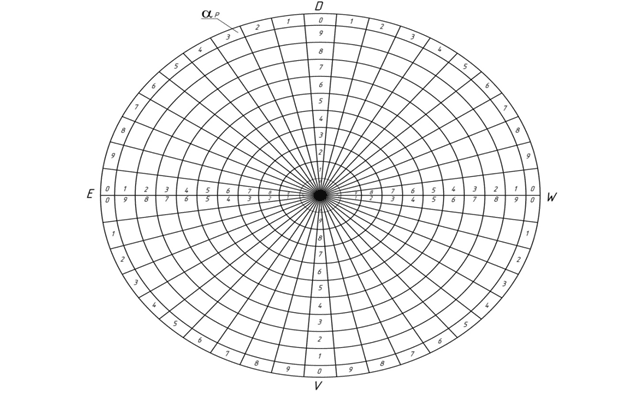
Рис. 2. Числовые параметры областей на плоскости

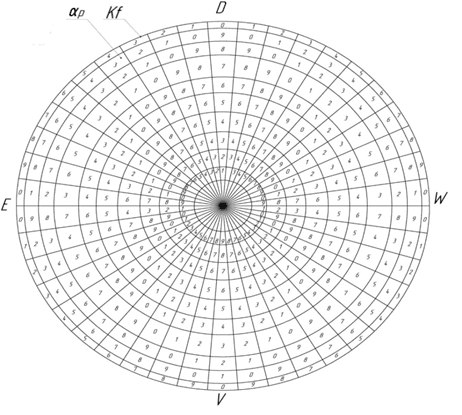
Рис. 3. Числовые параметры

Мы видим, что числовые ряды, лежащие на дугах, расположены таким образом, что максимум накладывается на минимум, к примеру, в особой точке W образуя в ней ноль.

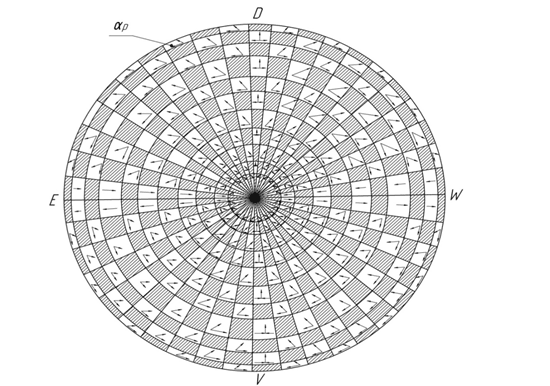
Рис. 4. Векторные параметры α_p

Все области пространства будут иметь числовую и векторную направленность (рис. 3, 4). На плоскости α_p можем наблюдать 2 тенденции движения:

• От центра, точки О к окружности Kf, в положительной части альфа, и от окружности Kf к центру к точке О в отрицательной части альфа.
• От прямой X (или OD) по дугам к прямой Y (или EW) в положительной части α_p и от прямой Y (или EW) к областям оси X (или VO), в отрицательной части α_p.

Рассмотрим фрагмент плоскостной геометрической структуры, элементы которой включают в себя ряды числовых значений (рис. 5).

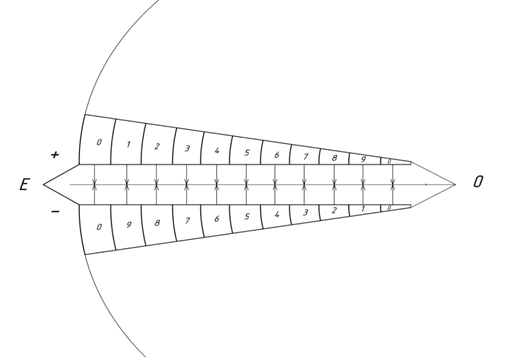
Рис. 5. Фрагмент плоскостной структуры для моделирования

Фрагмент состоит из центральной оси OE, назовем ее также ось Y, к которой с двух сторон примыкают области; каждой области присвоено определенное направление, обозначенное стрелкой. Видно, что прилегающие к оси области направлены друг к другу.

Области включают в себя числовые ряды от 1 до 9. В целом фрагмент представляет собой сектор большого круга, разделенный на более мелкие области радиусами круга и дугами окружностей [18].

Направленность числовых рядов находится во взаимозависимости с направленностью областей, в которых они находятся. Из рисунка 5 мы видим, что числовые ряды, прилегающие к оси Y, расположены, если так можно выразится, в числовой асимметрии. К примеру, область со значением 9 накладывается на 1, 8 на 2 и т.д. (Можно провести аналогию с тем, когда одноименные электрические заряды между собой отталкиваются, а разноименные притягиваются) [12].

В данном случае “притягиваются” не заряды, а области с разноименными числовыми значениями (“противоположными потенциалами”). Существенным свойством для нас является притяжение областей с противоположными числовыми потенциалами.

Мы видим, что числовые области граничат друг с другом таким образом, что наложение соответствующих числовых рядов друг на друга дает в сумме ноль по модулю 10. Точка E будет двусторонней, где максимум будет накладываться на минимум (max/min) [3].

1.2. Принцип моделирования на примере переключения внимания

Теперь предложенный фрагмент пространства попробуем связать с процессами из области физиологии, в частности, смоделируем некоторые составные части процесса мышления человека. Моделирование осуществим путем наложения существенных компонентов рассматриваемых процессов на наш фрагмент пространства.

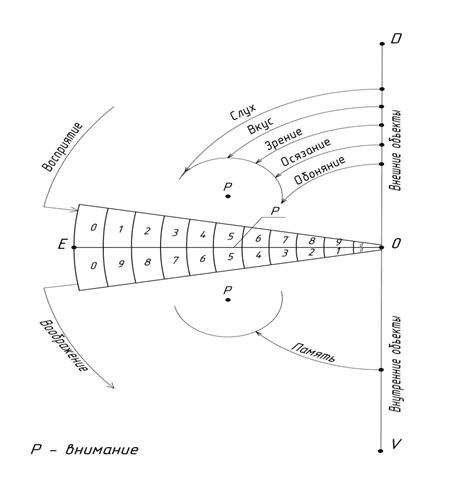
Рис. 6. Восприятие, воображение, внимание в соответствии с элементами моделирующего фрагмента

Для этого рассмотрим прямую Y (или OE) и области с прилегающими к ней числовыми рядами (рис.6).

Всю информацию мы условно можем классифицировать на 2 вида.

1. Информация, получаемая от внешних объектов в виде ощущений: зрительных, слуховых, вкусовых, обонятельных, осязательных, то есть восприятие [1]. Его мы свяжем с числовым рядом, прилегающим к положительной части OE, и заключим в интервале между двумя критическим точками (E + / O).
2. Информация, получаемая от внутренних объектов или из памяти, то есть воображение [17], которое свяжем с числовым рядом, прилегающим к отрицательной части EO и заключим в интервале между двумя критическим точками (E- / O). Эти два ряда являются параллельными и противоположно направленными.

Эти два числовых ряда наложены друг на друга таким образом, что максимум одного накладывается на минимум другого и наоборот (max/min).

Свяжем внимание с движением точки P по оси (Y).

В основе моделирования лежит гипотеза: возрастание внимания по отношению к внешним объектам сопровождается снижением внимания к внутренним объектам и наоборот.

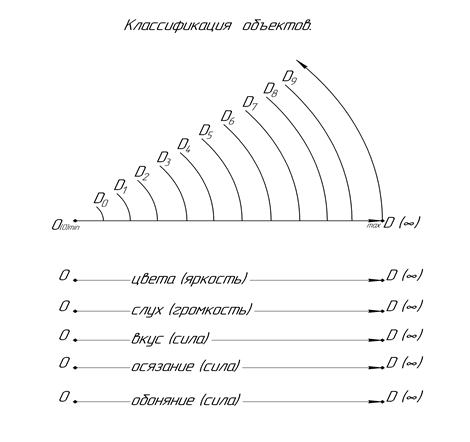
Рис. 7. Классификация внешних объектов

Теперь классифицируем объекты, воздействующие на наше сознание (рис. 7).

Цвета мы можем классифицировать в зависимости от яркости от минимальной к максимальной и заключим в интервал от O (0) → D (∞).

Звуки аналогичным образом классифицируем исходя из громкости от минимальной к максимальной и заключим в аналогичный интервал от O (0) → D (∞).

Вкусовые, обонятельные, осязательные ощущения, исходя из силы воздействия так же заключим в интервал от O (0) → D (∞).

Это лишь один из видов классификации, применяемый для описания нашего принципа моделирования.

Так же данные объекты (цвета, звуки, вкусовые, обонятельные, осязательные ощущения) мы можем классифицировать и по-другому, например, в зависимости от диапазона. К примеру, цвета (красный, оранжевый, зеленый, голубой, синий, фиолетовый) мы можем заключить в аналогичный интервал, с каждым цветом связав соответствующую точку в интервале от O (0) → D (∞) [5].

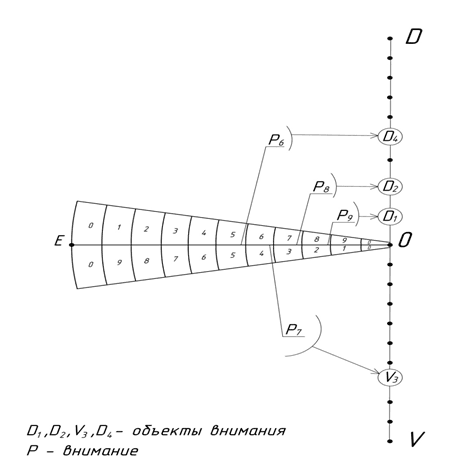
Рис. 8. Моделирование фрагмента процесса мышления

Теперь смоделируем фрагмент процесса мышления, исходя из поведения точки P на прямой OE, которая нами ранее была связана с вниманием (рис. 8).

Допустим, в момент времени t₁ внимание (P₉) сконцентрировано на внешнем объекте (D₁). С объектом (D₁) мы можем связать чашку кофе (объект вкусового характера). Внимание со значением – (P₉) направлено на объект с потенциалом (D₁).

В момент времени t₂ внимание (P₈) притягивает объект с большим потенциалом (D₂). С объектом (D₂) мы можем связать песню, звучащую по радио (объект звукового характера). Внимание со значением P₈ направлено на объект с потенциалом (D₂). Внимание переключилось с объекта (D₁) на объект (D₂) в силу того, что объект (D₂) обладал б льшим потенциалом относительно объекта (D₁), в момент времени t₂.

В момент времени t₃ внимание аналогичным образом (P₇) притягивает внутренний объект (V₃). Внимание со значением P₇ направлено на объект с потенциалом (V₃). С объектом (С₃) мы можем связать ассоциацию, вызванную внешним объектом (В₂). К примеру, музыка вызвала мысленный образ связанный, с воспоминанием о работе.

Внимание переключилось с объекта (D₂) на объект (V₃), так как объект (V₃) обладал б льшим потенциалом относительно объекта (D₂) в момент времени t₃.

В момент времени t₄ внимание становится (P₆) переключается на внешний объект (D₄). С объектом (D₄) мы свяжем ассоциацию, вызванную внутренним объектом (V₃).

К примеру, воспоминания о работе побудили субъекта открыть книгу соответствующей тематики. Внимание переключилось с объекта (V₃) на объект (D₄). В силу того, что объект (D₄) обладает б льшим потенциалом относительно объекта (V₃) в момент времени t₄ [19].

Таким образом, моделирование основано на гипотезе, что внимание всегда будет концентрироваться на объекте с б льшим потенциалом. Как было отмечено ранее, существенным свойством для нас является притяжение областей с противоположными числовыми потенциалами.

Мы видим, что описанные выше фрагменты, являются частными случаями проявления предложенной модели пространства (или пространства S), при помощи которого мы можем смоделировать комплексный процесс мышления. При этом каждую компоненту комплексного процесса моделируем при помощи одного из фрагментов пространства S, как описано выше (рис. 1).

1.3. Принцип моделирования на примере системы кровообращения человека

Рассмотрим систему кровообращения человека.

Кровь делится на венозную и артериальную [15], точно также как области пространства мы условно можем разделить на положительные и отрицательные.

Существует два круга кровообращения большой и малый [7].

Большой круг кровообращения начинается с того, что кровь из левого желудочка через аортальный клапан вбрасывается в аорту, после чего происходит разветвление на артерии, которые затем переходят в артериолы и многочисленные капилляры [16] (рис. 9).

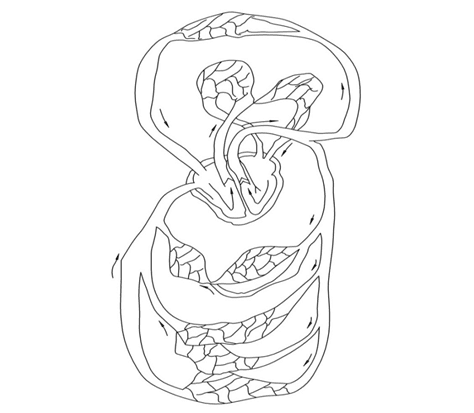
Рис. 9. Сердечно сосудистая система человека

Здесь мы можем аортальный клапан связать с особой выталкивающей точкой D модели пространства, а движение от аорты к капиллярам с направленностью областей на положительной полусфере S_p, от минимума – точки D к областям с большим числовыми значениями, к полюсам S и W (рис. 10 а, б). На рисунке 10 б, показаны векторные параметры сферической поверхности S_p, которая в свою очередь является составной частью модели нашего пространства [14].

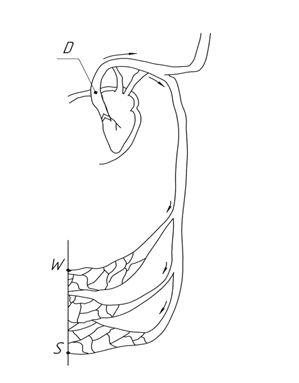
Рис. 10 а. Элементы системы кровообращения

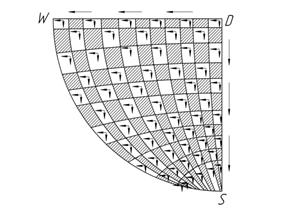
Рис. 10 б. Области на S_p в аналогии с системой кровообращения

Если мы рассмотрим данную фазу движения большого круга кровообращения на плоскостной структуре α, то аортальный клапан нами так же будет связан с особой выталкивающей точкой D, а движение от аорты к капиллярам мы свяжем с направленностью областей на α, от точки D – области с минимальным числовым значением по дуге DW к точке W – области плоскости α с максимальным числовыми значениями, в порядке возрастания числового потенциала (рис 11 а, б).

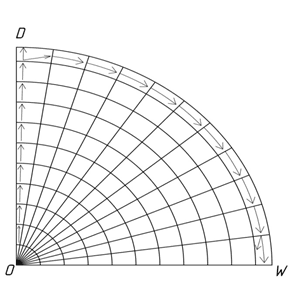
Рис. 11 а. Векторные параметры областей

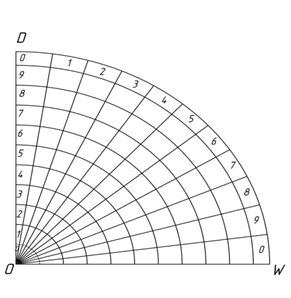
Рис. 11 б. Числовые параметры областей

Что происходит дальше? Кровь из капилляров переходит в венулы, кровь из артериальной становится венозной так как в капиллярах отдает кислород и меняет цвет. Этот переход мы свяжем с движением по оси Y от точки W к точке E и переходом через точку О, из положительных областей пространства в отрицательные (рис. 12 а,б).

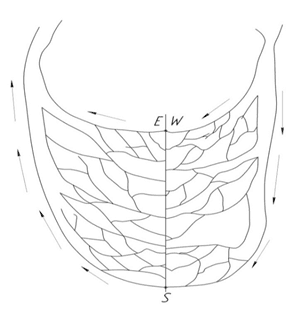
Рис. 12 а. Элементы системы кровообращения    

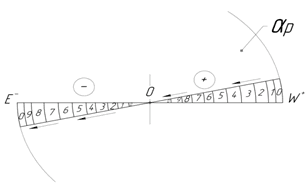
Рис. 12 б. Элементы пространства S в аналогии с системой кровообращения

Затем венулы собираются в вены, несущие кровь обратно в сердце [13, с. 4].

Данную фазу движения мы свяжем с направленностью областей на Sp^- от дуги SE к особой втягивающей точке V. (рис 13 а,б) На рисунке 13 б, показаны элементы сферической поверхности S_p.

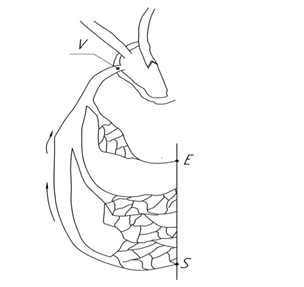
Рис. 13 а. Элементы системы кровообращения    

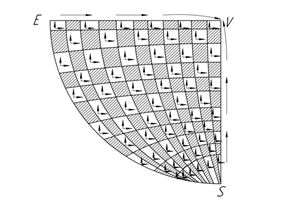
Рис. 13 б. Области на S p в аналогии с системой кровообращения

Если рассмотреть данную фазу движения большого круга кровообращения на плоскости α, то движение венозной крови от венул через вены в правое предсердие нами будет связано с направленностью областей на отрицательной части плоскости α, от точки E – области с минимальным числовым значением, по дуге EV к особой втягивающей точки V, которая находится в области с максимальным числовым значением, движение происходит в порядке возрастания числового потенциала (рис 14 а,б).

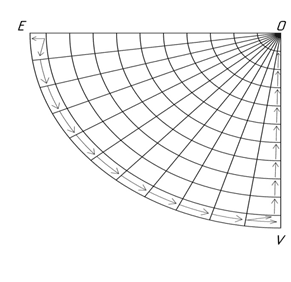
Рис. 14 а. Векторные параметры областей    

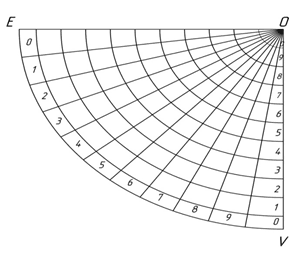
Рис. 14 б. Числовые параметры областей

Восточную часть прямой VO и области к ней прилегающие (элемент 4) (рис. 15 б) мы отождествим с правым предсердием, а правый желудочек рассмотрим в аналогии с областями, прилегающими к восточной части прямой ОD (элемент 3, рис. 15 б).

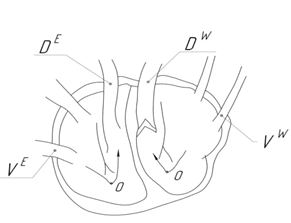
Рис. 15 а. Сердце в аналогии с элементами пространства S    

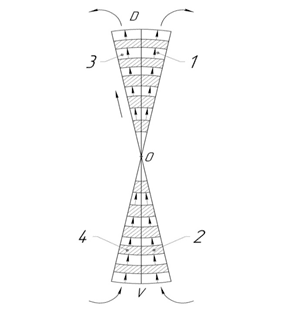
Рис. 15 б. Элементы в пространства S аналогии с сердцем

В свою очередь, области западной часть прямой VО мы свяжем с левым предсердием (элемент 2), а левый желудочек рассмотрим в аналогии с областями западной части прямой ОD (элемент 1) (рис. 15 б) [14].

Предсердно-желудочковые клапаны левого и правого предсердия и желудочка мы отождествим с точкой О (рис. 15 а).

На правом желудочке заканчивается большой и начинается малый круг кровообращения, в правый желудочек сердца переходит вся венозная кровь, поступившая из правого предсердия [20].

Началом малого круга кровообращения является легочный ствол, который при подходе к легким разветвляется на правую и левую легочные артерии. Они несут к альвеолам легких венозную кровь, которая отдав углекислый газ и получив взамен кислород, становится артериальной. Насыщенная кислородом кровь по легочным венам (по две с каждой стороны) поступает в левое предсердие, где и заканчивается малый круг кровообращения (рис. 9) [6].

В аналогии с тем, как мы рассматривали фазы большого круга кровообращения в контексте с элементами модели пространства S, элементы малого круга кровообращения мы наложим на соответствующие элементы модели S.

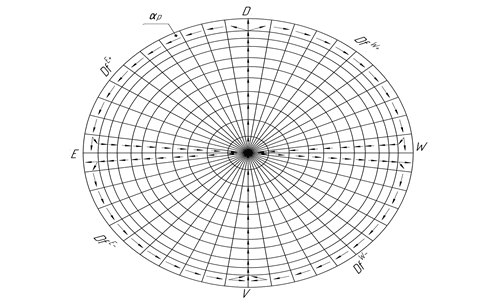
Рис. 16. Геометрическое пространства для моделирования комплексных процессов

Так в частности начало малого круга кровообращения, легочный ствол и правую и левую легочные артерии свяжем с направленностью областей на плоскости α от точки D по дуге DE к точке E.

Фазу малого круга кровообращения, в которой происходит переход крови из венозной в артериальную, нами будет связана с движением по оси Y от точки E к точке W и переходом через точку О, из положительных областей пространства в отрицательные.

Легочные вены и поступление крови в левое предсердие мы свяжем с направленностью областей отрицательной части плоскости α от точки W по дуге WV к точке V (рис. 16).

Затем кровь поступает в левый желудочек, откуда берет начало большой круг кровообращения [9].

Мы видим, что описанные выше комплексные процессы сердечно-сосудистой системы человека накладываются на модель предложенного пространства. Каждая компонента комплексного процесса моделируется при помощи одного из фрагментов общей модели пространства (рис.16).

1.4. Принцип моделирования на примере процессов электродинамики

В целях выявления общей структуры природных процессов, которая прослеживается в различных областях знаний, рассмотрим пример из области электродинамики.

Для этого геометрию нашего пространства S свяжем с электромагнитными процессами.

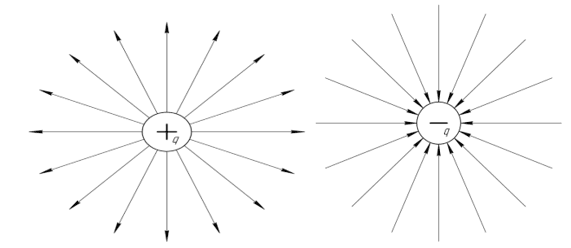
Рис. 17. Векторная направленность положительного и отрицательного зарядов

На рисунке 17 видно, что векторы напряженности положительного заряда [10] направлены от центра к периферии, и наоборот векторы отрицательного заряда направлены от периферии к центру (рис. 17).

Векторы напряженности положительного точечного заряда [12] будут находится в аналогии с направленностью областей на положительной полусфере Sp⁺ от минимума – точки D к областям с большими числовыми значениями ∈ γ_p. На рисунках 18 а, б, показаны векторные и числовые параметры сферической поверхности Sp,которая в свою очередь является составной частью нашего пространства S.

В свою очередь векторная направленность отрицательного точечного заряда [12] будет находится в аналогии с направленностью областей на отрицательной полусфере Sp^- от областей окружности с минимальными числовыми значениями ∈ γ_p к точке V которая находится в области с максимальным числовым значением (рис. 19 а, б).

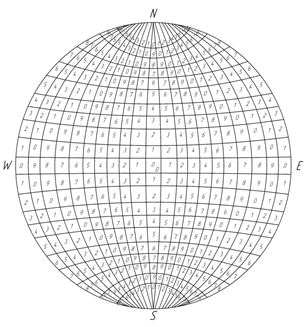
Рис. 18 а. Числовые параметры Sp +    

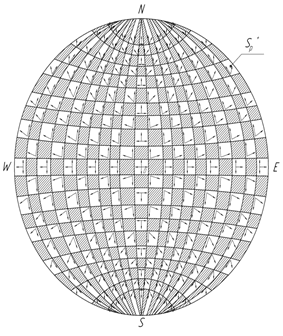
Рис. 18 б. Векторные параметры Sp +

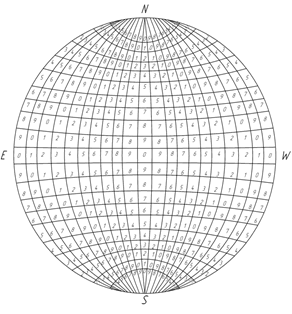
Рис. 19 а. Числовые параметры Sp^-    

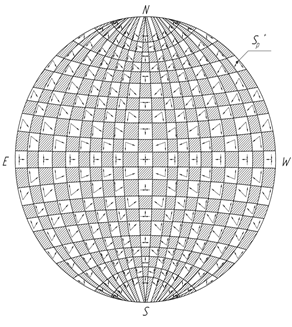
Рис. 19 б Векторные параметры Sp^-

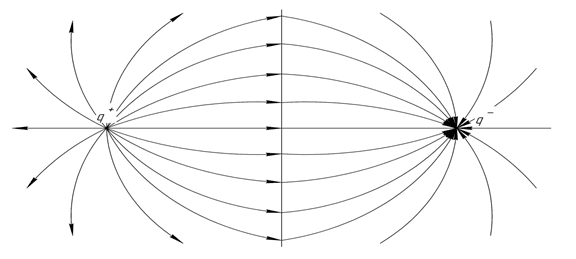
Рис. 20. Векторы напряженности электростатического поля

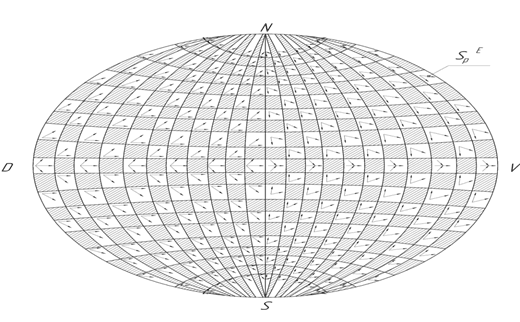
Рис. 21. Векторная направленность S_p^E

Векторы напряженности электростатического поля [12] находятся в аналогии с направленностью областей восточной полусферы Sp от положительного полюса – точки D к областям ∈ дуге SN и от областей ∈ дуге SN к отрицательному полюсу – точке V (рис. 20, 21).

Часть 2. Параметры, структура и координаты модели геометрического пространства

2.1. Структура модели пространства

В первой части работы нами уже рассмотрены отдельные элементы модели геометрического пространства и показан принцип построения математической модели, теперь для представления полной картины мы детально опишем структуру созданной модели пространства.

За основу для нашего анализа было взято трехмерное пространство R³ [19]. Известно, что координаты в пространстве определяются относительно трех координатных прямых, обозначим их как Ox^R; Oy^R; Oz^R (рис. 22).

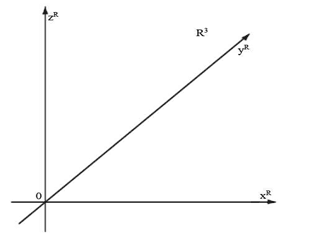
Рис. 22. Система координат в пространстве R³

Область в R³ ограничим сферой S_p, а центр этой сферы отождествим с началом координат точкой О. Радиус S_p может находится в интервале (0/∞). Тогда область ограниченная S_p будет представлять собой замкнутое пространство и обозначаться через S (рис. 23).

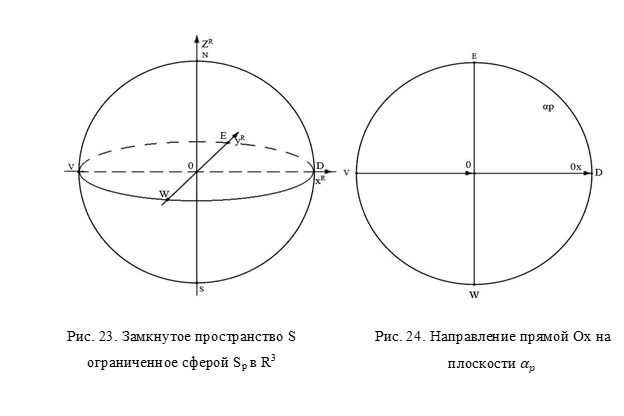
Каждая из осей OxR; OyR; OzR пересечет сферу Sp ровно в двух диаметрально противоположных точках (рис 23).

Тогда прямые пространства R3 xR; yR; zR определят прямые x; y; z в пространстве S, которые представляют собой хорды. Ранее мы отмечали, что прямая x будет направлена от точки V к точке D (рис. 24).

Теперь на каждой из шести полухорд мы отложим по 10 единичных точек (рис. 25), которые поделят каждую из них на 11 единичных отрезков.

1) D₀; D₁ … D₉; D  OD; 2) V; V₀; V₁ … V₉  OV;

3) W₀; W₁ … W₉; W  OW; 4) E₀; E₁ … E₉; E  OE;

5) S₀; S₁ … S₉; S  OS; 6) N₀; N₁ … N₉; N  ON.

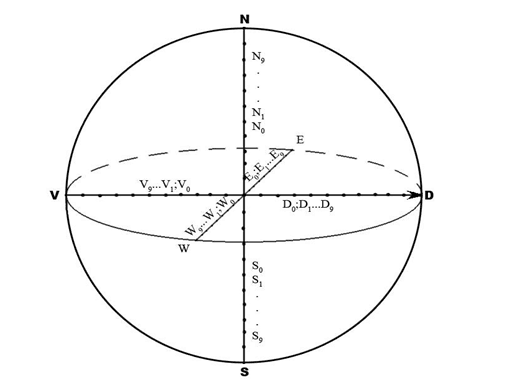
Рис. 25. Единичные точки на координатных прямых в S

Каждые из двух осей координат определяют плоскость α_p; β_p γ_p суть круг. Они поделят шар на 8 актантов (рис. 26).

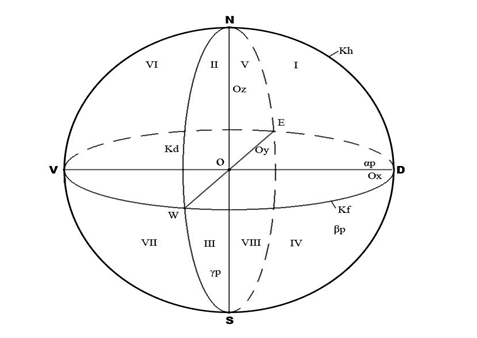
Рис. 26. Координатные плоскости α_p; β_p γ_p  в S, актанты

Каждая такая плоскость перечет сферу S по окружности Kf; Kh и Kd соответственно. Сферу S плоскость γ_p условно поделит на два полушария положительное S⁺ и отрицательное S^- с полюсами D и V.

На сфере S_p зададим координаты относительно двух дуг. На полусфере Sp⁺ это дуги Df⁺ и Dh⁺ на Sp^- дуги Df^- и Dh^- (рис. 27 а, 27 б).

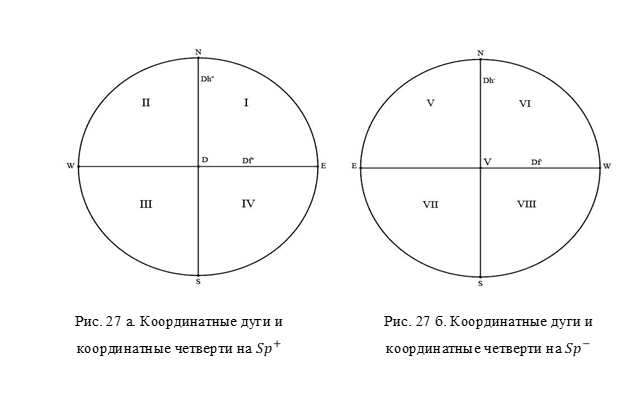
Дуги поделят сферу на четверти. На каждой из полу дуг выбрано направление. На Sp⁺ движение дуг направлено от т. D к точкам принадлежащих окружности Kd; на Sp^- движение координатных дуг направлено от точек, принадлежащих окружности Kd к т. V (рис. 28).

В пространство S ограниченное сферой Sp вписано десять других сфер меньших радиусов, центр каждой сферы будет лежать в т.О.

Потребуем, чтобы точки пересечения сфер с осями координат накладывались на соответствующие единичные точки координатных прямых (рис. 29).

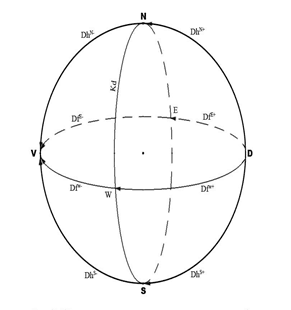
Рис. 28. Направление координатных полудуг на Sp    

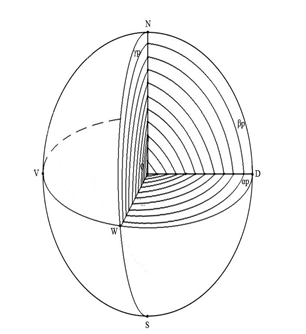
Рис. 29. Параметры пространства после вписания в них десяти сфер

Пересечем пространство S двадцатью плоскостями параллельными  каждая из этих плоскостей будет касательной к соответствующей сфере в северном или южном полюсе (рис. 30).

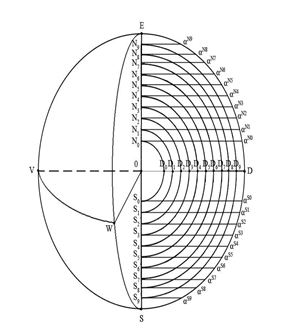
Рис. 30. Пересечение шара S двадцатью плоскостями    

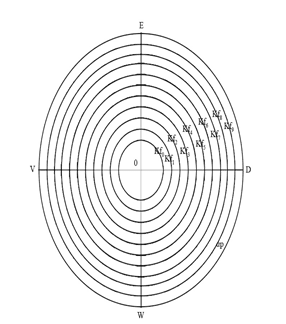
Рис. 31. Семейство окружностей на α_p

В результате такого пресечения в горизонтальных плоскостях образуется семейство окружностей [2] (рис. 31).

Каждая из 20-ти плоскостей семейства α пересечет Sp по окружности, тем самым определяя на ней семейство параллелей.

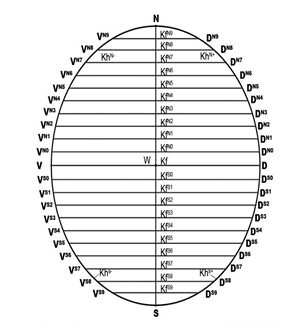
Рис. 32 а. Единичные точки на координатных дугах семейства V и D

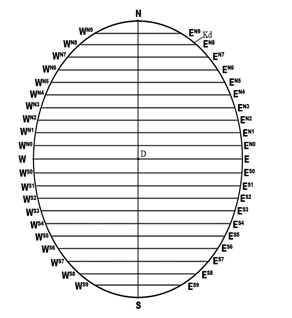
Рис. 32 б. Единичные точки координатных семейства W и E

Точки пересечения параллелей с дугами координат будут являться единичными точками этих координатных дуг [11] (рис. 32а; 32 б).

Теперь пересечем сферу S двадцатью осевыми плоскостями семейства β. Плоскости будут пересекаться друг с другом по оси Oz и располагаться под равными углами относительно друг друга. В результате такого пересечения плоскость α_p примет следующие параметры (рис. 33).

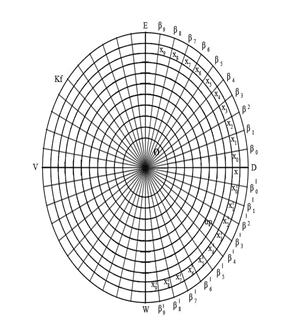
Рис. 33. Параметры после пересечения двадцатью плоскостями семейства    

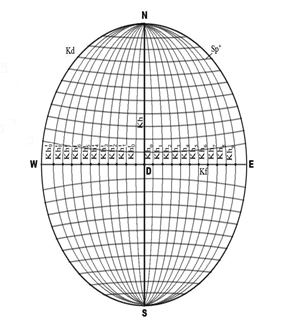
Рис. 34. Криволинейная сеть на Sp

Каждая из 20-ти плоскостей семейства β пересечет Sp по окружности, определив на ней семейство меридианов (рис. 34). Меридианы пересекут координатные дуги на Sp в десяти единичных точках (рис. 35).

Теперь мы опустим момент наличия в сечениях плоскостей семейства β окружностей и тогда эти плоскости примут следующие параметры (рис. 36).

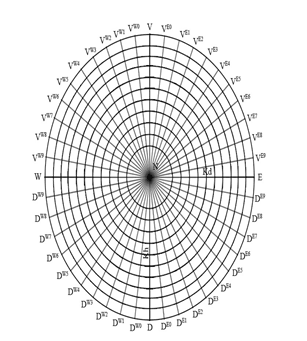
Рис. 35. Единичные точки на координатных дугах круга Kf    

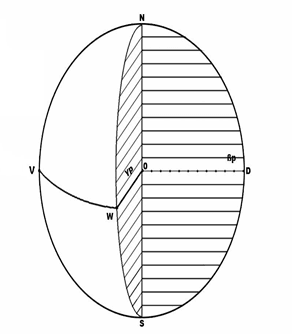
Рис. 36. Параметры вертикальных плоскостей на примере β_p γ_p

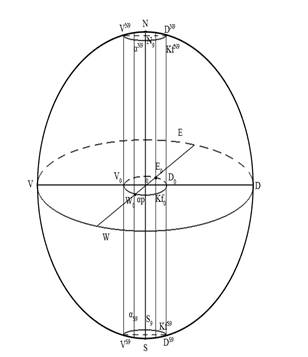
Рис. 37. Цилиндр в пространстве S    

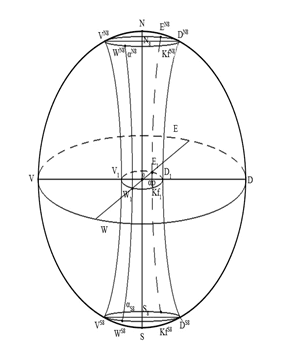
Рис. 38. Гиперболическая поверхность в S

После чего, мы соединим окружности принадлежащие α_p с соответствующими параллелями на Sp^N;S (рис. 37, 38, 39).

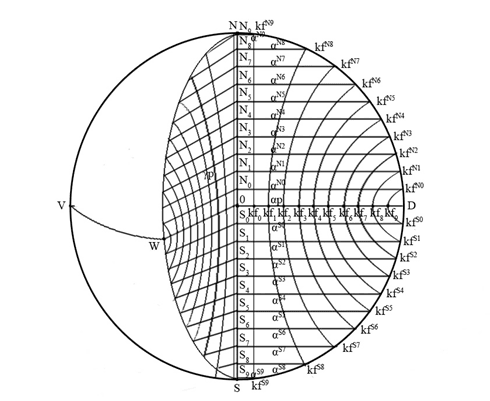
Рис. 39. Преобразование шара S в вертикальных плоскостях на примере β_p γ_p

2.2. Система координат в пространстве S

Нами определена координатная сеть в пространстве S.

Теперь рассмотрим принципы, в соответствии с которыми определяются координаты в нашем пространстве.

В предлагаемой системе координат каждой точке пространства сопоставляется тройка чисел, а точнее букв, которые и будут являться ее координатами.

Первая координата (x) для точки будет определена относительно оси Ox так: x = D₂ – для точки 1; x = V₃ – для точки 2; x = 0 – для точки 3 (рис. 40).

Третья координата (z) будет определятся относительно оси Oz.

z =N₁ – для точки 1; z = S₂ – для точки 2; z = 0 – для точки 3 (рис. 40).

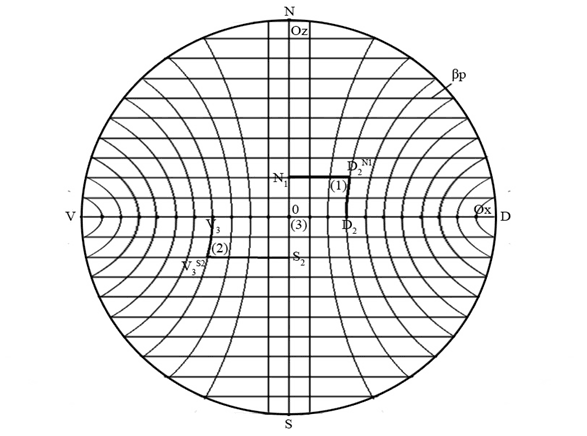
Рис. 40. Определение координат по отношению к координатным осям Ох и Oz

В этом отношении для Ox и Oz метод схож с методом декартовой системы координат, в нашем случае координатная сеть на β будет искривлена и ограничена окружностью Kh, но таким образом мы можем определить координаты только на плоскости β_p.

Вторая координата (y), в частности на плоскости α_p, будет определятся в зависимости от единицы смещения относительно оси Ox в сторону оси Oy.

В пространстве S в целом координата (y) будет определятся в зависимости от единицы смещения относительно плоскости β_p в сторону плоскости γ_p.

В зависимости от единицы смещения (y) на плоскости α_p будет равен, для точки (1) у = W₁; для точки (2) y = E₆; для точки (3) у = W₇; для точки (4) y = E₂ (рис. 41).

Этот метод схож с методом определения координат в цилиндрической системе координат.

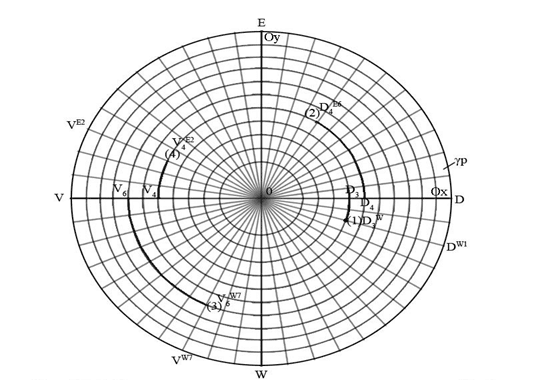
Рис. 41. Определение координаты (у) относительно Ох

Система координат на сферической поверхности Sp находится во взаимосвязи с системой координат в пространстве S.

Координата (x) на Sp⁺ будет определятся в зависимости от единицы смещения относительно оси Ox. Для точки (1) x = D₅, для точки (2) x =D₇ (рис. 42).

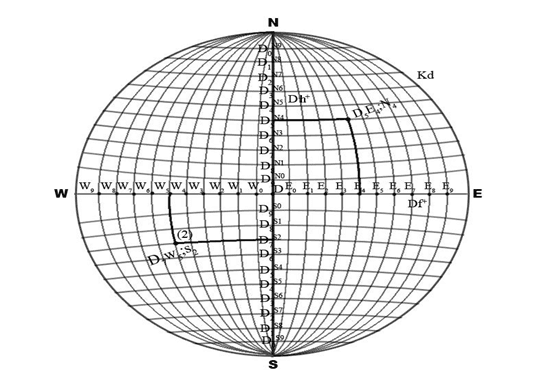
Рис. 42. Определение координат на Sp⁺

Вторая координата (y) в частности на Sp⁺ определяется относительно дуги Df⁺ в зависимости от единицы смещения от дуги Dh⁺ принадлежащих β_p. в сторону окружности Kd принадлежащую γ_p. Для точки (1) y = E₄; для точки (2) y = W₅.

Третья координата (z) на Sp⁺ определяется относительно дуги Df⁺ в зависимости от единицы смещения от оси Oz в сторону Северного или Южного полюсов. Для точки (1) z = N₄; для точки (2) z = S₂ (рис. 42).

В случае когда точка находится в γ_p то ее координаты определяются уже относительно двух осей Oy и Oz и будут обозначатся для точки (1) E₀ S₁ для точки (2) W₇ N₂ (рис. 43).

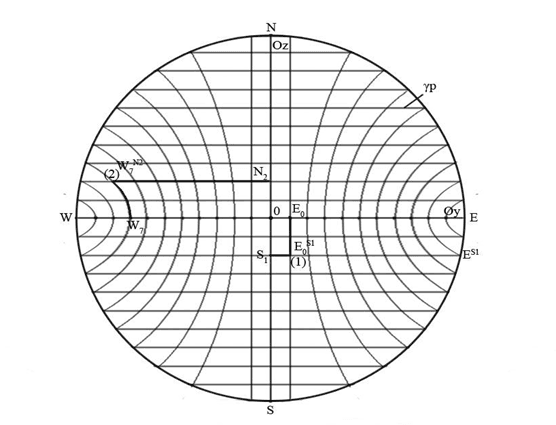
Рис. 43. Координаты на плоскости

Координаты точек мы будем записывать следующим образом. Первой обозначается абсцисса (x), она всегда будет обозначатся заглавной буквой. К примеру, D₁ в S⁺ или V₃ в S^- ; второй обозначается ордината ( у ). К примеру, D₁ E₇ или V₃ W₈. Третьей обозначается аппликата ( z ). К примеру, D₁ E₇ N₅ или V₃ W₈ S₁ [8].

2.3. Вопросы философии математики в контексте с моделью пространства

Итак, ране мы отмечали, что координаты в трехмерном пространстве R³ определяются относительно трех координатных прямых, которые нами обозначены как Ox^R; Oy^R; Oz^R (рис. 44).

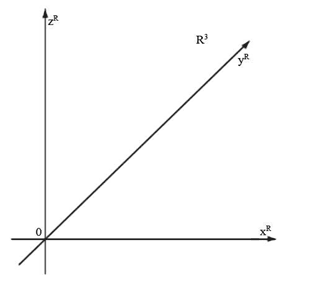
Рис. 44. Система координат в пространстве R³

Специфика прямоугольной системы координат заключается в том, что она фактически описывает собой пространство куба или если мы говорим о плоскости, то это квадрат (рис. 45, рис. 46).

К примеру, если в пространстве R² мы проведем окружность S₀ с центром в точке О и радиусом R₀ тогда все точки заключенные в область данной окружности будут являться бесконечным множеством. Теперь если мы проведем окружность S₁ большего радиуса R₁ так же с центром в точке О, тогда R₁ = R₀ + ∆R. Все множество точек заключенное между S₀ и S₁ мы примем за единицу, тогда площадь, ограниченная окружностью S₁, будет равна (∞ + 1) (рис. 47).

Рис. 45. Форма пространства R³

Рис. 46. Форма пространства R²

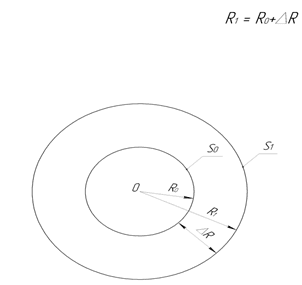
Рис. 47. Окружности S₀ S₁

Аналогичным образом мы можем провести окружности больших радиусов R₂; R₃ … и т.д. В итоге, с таким возрастающим движением от центра О к периферии мы свяжем расширение окружности S_p данное расширение пространства R² будет сопровождаться движением по оси Ox^R точки D, которая ∈ S_p.

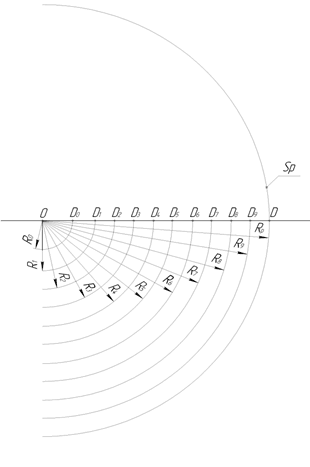
Рис. 48. Семейство из 11-ти окружностей на плоскости в R²

Таким образом с точкой D мы можем связать потенциальную бесконечность, то есть радиус окружности S_p может колебаться в интервале от 0 до  (рис. 48).

Из рисунка 48 видно, что ось Ox^R определит прямую ОD.

В свою очередь на прямой OD будет отложено десять единичных точек D₀; D₁ … D₉. Каждой такая единичная точка будет принадлежать окружности соответствующего радиуса R₀; R₁ … R₉; R_p.

Мы видим, что любое изменение радиуса R_p и движение точки D по прямой Ox^R к центру О либо к периферии будет сопровождаться пропорциональным изменением масштаба между семейством единичных точек на прямой OD.

Расширение окружности S_p с одной стороны сопровождается увеличением радиуса R_p, а с другой стороны будет сопровождаться увеличением длины окружности S_p.

Такое изменение длины окружности мы свяжем с отклонением относительно оси OD в сторону т. W либо в сторону т. E и движением по дуге окружности S_p точки D (рис. 49).

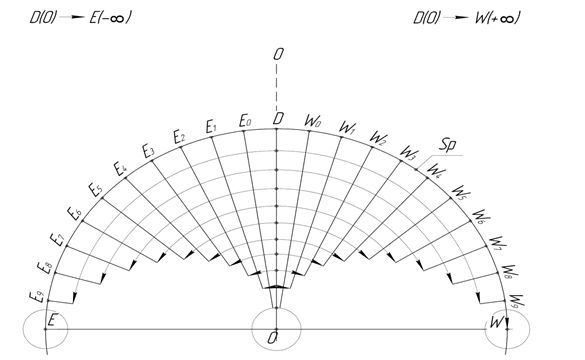
Рис. 49. Направление дуг относительно точки D

Тогда ось OD и в частности точка D нами, в данном случае, будет принята за ноль, а смещение точки D по дуге DW ∈ S_p будет сопровождаться стремлением к т. W, которая будет выполнять функцию потенциальной бесконечности. На дуге DW будет отложено десять единичных точек W₀; W₁ … W₉; W, аналогичным образом на дуге DE так же будет отложено десять единичных точек E₀; E₁ … E₉; E.

Таким образом ось OD будет выполнять роль своеобразной зеркальной оси, и выступать осью симметрии в отношении Восточной и Западной областей круга S_p. Мы видим, что точки E и W, будут находится на одной прямой с точкой О, это будут предельные точки, к которым может стремится движение по соответствующим дугам от точки D на окружности S_p.

Мы можем наблюдать четыре критические точки, между которыми заключено расширение окружности S_p.

В свою очередь мы видим, что с точкой О относительно прямой OD нами связан ноль, соответственно с точкой D ранее мы связали (+ ∞). Вместе с тем, относительно дуг DW и DE точка D будет выполнять функцию нуля. То есть точка D будет двусторонней точкой и выполнять противоположные функции. Если точка D связана с нулем, тогда с точкой E логично связать (- ∞), а с точкой W (+ ∞) на окружности S_p (рис. 49).

Элементы круга S_p ограниченные осью EW с полюсом D мы примем за положительную часть круга S_p и обозначим как S_p⁺.

Продолжая логику, с областями окружности S_p которые будут находится в противоположной части окружности относительно S_p⁺ мы свяжем круга S_p и обозначим как S_p^-.

Если OD выполняет функцию оси симметрии, тогда ось OW выполнит функцию оси асимметрии и все элементы ∈ S_p^- будут иметь противоположную направленность относительно S_p⁺ (рис. 50).

Отрицательная часть оси Ox^R будет направлена от полюса V к точке О.

Аналогичным образом, на прямой VO, нами будет отложено десять единичных точек V₀; V₁ … V₉; О. В свою очередь, на дуге WV, которая направлена соответственно от точки W к точке V, так же будет отложено десять единичных точек E₀; E₁; … E₉; V.

Теперь мы видим, что каждая такая критическая точка O, D, W, V будет выполнять роль двусторонней точки, где максимум накладывается на минимум (max/min) или ноль на бесконечность (0/∞).

Функция отрицательной стороны круга S_p состоит в том, что его элементы выполняют роль своеобразного равновесия, то есть каждому движению точки на S_p⁺ будет соответствовать противоположное движение на S_p^- (рис 50).

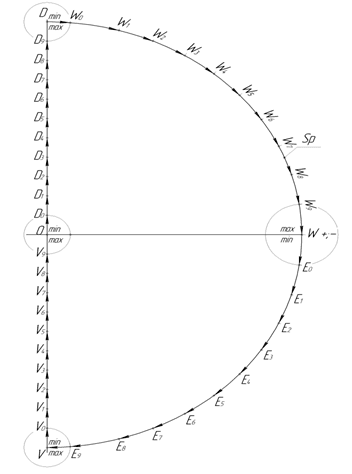
Рис. 50. Критические точки окружности S_p

Характерной чертой прямоугольной системы координат является то, что пространство измеряется относительно статичных или фиксированных точек. Предлагаемая нами модель предполагает измерять пространство системой координат, которая находится в динамике.

Заключение

В работе показан принцип математического моделирования посредством наложения структуры рассматриваемых процессов на модель нашего пространства, рассмотрен пример моделирования фрагмента процесса мышления человека, рассмотрен процесс функционирования сердечно-сосудистой системы человека, описаны отдельные процессы электродинамики.

Несмотря на обширный объем материала по вопросу математического моделирования в области физиологии в целом и процесса мышления в частности, перехода на качественно новый уровень в изучении данных сложнейших процессов нашего сознания на сегодняшний день добиться не удается.

Большинство исследователей считают возможность использования математического аппарата в частности при описании психических процессов нашего сознания весьма отдаленной перспективой.

Предложенный подход позволяет производить моделирование комплексных физиологических процессов, выявляя их общую и взаимозависимую природу.

Для нас является важным показать общую структуру процессов в различных областях знаний, проследить закономерности, которые присутствуют в процессах мышления человека, процессах функционирования сердечно-сосудистой системы человека, а также в отдельных процессах электродинамики, в теории чисел.

Все изложение материала было произведено при минимальном использовании математического аппарата, что придает работе б льшую доступность для понимания.

Рассчитываем, что предложенные идеи внесут новый импульс в изучение и понимание рассмотренных вопросов.