Введение
Вероятностные (стохастические) модели представляют собой математические модели, основанные на отображении системы с помощью случайных событий, процессов, которые описываются соответствующими вероятностными (статическими) характеристиками и закономерностями. На различных этапах моделирования сложной технической системы используются математические модели, усложняющиеся по мере их проработки. При поиске оптимального варианта для получения искомого результата приходится многократно проводить эксперимент с учетом многомерности и многокритериальности задачи [1, c.10]. А на заключительных этапах моделирования часто используют вероятностные модели для того, чтобы исследовать процессы функционирования технической системы в условиях, максимально приближенных к реальным с использованием статистических методов обработки результатов. В связи с этим существует потребность в инструменте, позволяющем обрабатывать данные, полученные в ходе моделирования. Решением проблемы может быть создание вероятностного калькулятора, который может быть полезен для проведения научных и инженерных расчетов.
В статье рассматриваются основные теоретические аспекты разработки библиотеки классов, которая может быть использована для работы со случайными величинами в приложениях, исполняемых на программной платформе .NET Framework.
Объекты и методы исследования
Объектом исследования являются одномерные случайные величины. Предметом исследования является выполнение арифметических операций с одномерными случайными величинами.
Случайной называется величина, которая в результате испытаний принимает то или иное (но при этом только одно) возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. Будем обозначать случайные величины как X, Y, а их возможные значения – x, y и т.д. Совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет закон распределения, который может быть задан в виде таблицы, функции распределения F(x) или плотности распределения p(x).
Разрабатываемая библиотека классов позволяет выполнять вычисления со случайными величинами как с обычными переменными компьютерной программы. Пусть f, g – функции плотности распределения независимых случайных величин X и Y соответственно. Величины X+Y, X-Y, X×Y, X/Y формируются в результате выполнения арифметических операций над X и Y. Арифметические операции над функциями плотностей будем обозначать как f⊕g, f⊝g, f⨀g и f⊘g.
Ниже описано, каким образом определяются плотности, возникающие в результате арифметических операций над независимыми случайными величинами.
Функция плотности распределения суммы X+Y двух независимых случайных величин X и Y – формула (1):
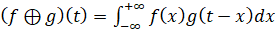 . (1)
. (1)
Функция плотности распределения разности X-Y двух независимых случайных величин X и Y – формула (2):
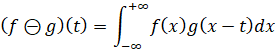 . (2)
. (2)
Функция плотности распределения произведения X×Y двух независимых случайных величин X и Y – формула (3):
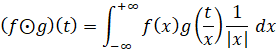 . (3)
. (3)
Функция плотности распределения частного X/Y двух независимых случайных величин X и Y – формула (4):
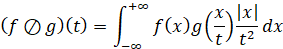 . (4)
. (4)
Если u – функция, состоящая из n строго монотонных и дифференцируемых частей ui, то распределение u(X), где X – СВ с функцией плотности f, задается как
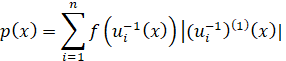 , (5)
, (5)
где u-1 обозначает функцию, обратную к функции u, а u(1) – первую производную функции u.
Требуется, чтобы функции плотности распределений и указанное количество их производных были ограниченными и непрерывными, за исключением конечного числа точек, в которых в которой функция не определена или имеет нерегулярное поведение. Такие точки будем называть потенциальными особыми точками (потенциальными сингулярностями) функции плотности. При этом необязательно, чтобы функция плотности (или ее производная) имела сингулярность в данной точке. Важным является следующее требование: вне особых точек функции плотности и определенное число их производных должны быть непрерывными (и, следовательно, ограниченными в пределах малых окрестностей особых точек).
Обозначим семейство функций распределений как Fk, k∈N. Будем говорить, что функция распределения f принадлежит семейству Fk, если существует n∈N и точки p1,…,pn∈R, , называемые потенциальными особыми точками, такие, что для всех 0 ≤ i ≤ k функция f(i) непрерывна во всех точках за исключением потенциальных особых точек p1,…,pn.
Операции над величинами реализуются в библиотеке классов на основе теоремы, представленной в работе [2, с.5]. Например, если f∈Fk и f∈Fk – функции плотностей распределения с потенциальными особыми точками p1,…,pn и q1,…,qm соответственно, то f ⊕ g ∈ Fk с потенциальными особыми точками pi+qi, 1 ≤ i ≤ n, 1≤ j ≤ m. Кроме того, в работе [2] приводится ряд теорем и доказательств относительно вычисления результата арифметических операций над функциями плотностей случайных величин. К одним из основных результатов данной работы является теорема, которая утверждает, что семейства Fk замкнуты относительно всех арифметических операций, а также для операции возведения в степень.
Точка сингулярности в нуле имеет особое значение для операций умножения и деления: функции суммы и разности ограниченных функций плотности остаются ограниченными, а произведения и частные могут давать особую точку в нуле. Например, на рис. 1 приведен график функции плотности произведения двух независимых нормально распределенных случайных величин, полученный с использованием библиотеки классов, а на рис. 2 – график функции распределения. Функции плотности, имеющие единственную потенциальную особую точку в нуле, образуют подсемейства Fk, замкнутые по четырем арифметическим операциям и операции возведения в степень.
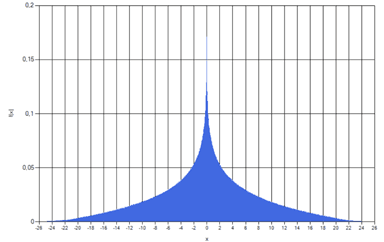
Рис. 1. График функции плотности произведения двух стандартных нормальных распределений
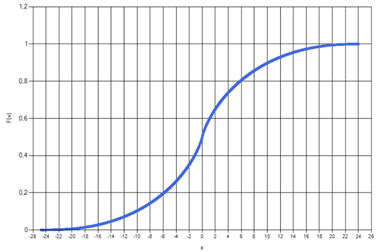
Рис. 2. График функции распределения произведения двух стандартных нормальных случайных величин
Потенциальные особые точки определяют интервалы, на которых результирующая функция будет аппроксимирована. Для выполнения процедуры аппроксимации функция плотности вычисляется в конечном количестве точек. Каждое такое вычисление выполняется путем применения численного интегрирования по одной из формул (1)-(4). В данном случае можно использовать алгоритм вычисления линейной свертки дискретных последовательностей.
Распределения случайных величин представляются в виде кусочно-заданных полиномиальных приближений их функций плотности. Под кусочно-заданной понимается функция, определенная на множестве вещественных чисел, заданную на каждом из интервалов, составляющих область определения. Те точки, которые делят область определения функции на составляющие, называются граничными точками и являются по сути точками разрыва функции.
Каждая аппроксимированная (приближенная) часть функции называется сегментом. Крайние точки сегментов располагаются в потенциальных особых точках, а также в точках +∞ и -∞. Предполагается, что каждый из сегментов принадлежит к одному из следующих видов: сегмент на замкнутом интервале без особых точек, сегмент на замкнутом интервале с особой точкой на одном из его концов или сегмент без особых точек и с одной из крайних точек в плюс или минус бесконечности.
Каждая из аппроксимируемых функций плотности сопоставлена с набором потенциальных особых точек, в которых поведение функции неизвестно. Во-первых, нужно определить, действительно ли потенциальная особая точка является особой точкой. Если это так, то нужно выбрать методы для максимально точного представления функции в данной точке.
Если функции плотностей распределения величин, над которыми выполняются арифметический операции, имеют особые точки, невозможно заранее определить, будет ли иметь особые точки результирующая функция. К примеру, сумма двух независимых случайных величин с функциями плотности f(x)=0.25x-0.75 на [0,1] имеет особую точку в нуле, в то время как сумма двух распределений хи-квадрат с количеством степеней свободы 1 не имеет особых точек. Поэтому следует пытаться определить наличие особых точек численно.
Заключение
Разработка иерархии классов для работы с одномерными случайными величинами продолжается. В частности, открытыми остаются такие вопросы, как оценка погрешности численных методов интерполяции и интегрирования, а также исследование изменения количества потенциальных особых точек в результате выполнения множественных арифметических операций.
Практическая значимость исследования заключается в возможности применения иерархии классов для проведения научных и инженерных расчетов (например, в задачах прогнозирования транспортных потоков, стохастических финансовых операций и т.п.). Библиотеку классов можно использовать как средство для выполнения арифметических операций над различными случайными величинами из таких параметрических семейств, как, например, равномерное, нормальное, экспоненциальное, а также выполнять построение их функций плотности и распределения и вычислять их основные числовые характеристики (математическое ожидание, дисперсия, асимметрия, эксцесс и т.д.).

.png&w=640&q=75)