Введение
В инженерной практике важную роль играет точность выполняемых расчетов. От этого может зависеть, например, выгода предприятия, а также здоровье и безопасность сотрудников на производстве. Зачастую расчеты проводятся не с точными значениями величин, а только с их приближенными (округленными) значениями. Причем может оказаться, что начальное округление данных было слишком грубым, в результате был получен неадекватный результат. Это приводит к тому, что приходится производить все расчеты заново, что зачастую является причиной потери лишнего незапланированного времени и затрате лишних трудовых ресурсов [3, c. 65]. В крупных проектах подобная ситуация может привести к затягиванию сроков сдачи проекта, следовательно, к недовольству пользователей или вовсе к срыву контракта, что приводит к плачевным последствиям. Для того, чтобы избежать подобной ситуации в данной статье предлагается описание алгоритма клиент-серверных чисел, который позволяет быстро произвести перерасчет всего дерева операций для гибкого управления точностью конечного числа.
Теоретические аспекты
На практике часто невозможно получить истинное значение величины, и вычисления проводятся с ограниченным количеством значащих цифр. Значение, которое используется вместо истинного с той или иной степенью достоверности называется приближённым значением данной величины [2, c. 3]. Существуют иррациональные, алгебраические числа, рациональные с периодической или бесконечной дробной частью, такие числа записываются приближенно, т.е. заменяются другими, близкими по значению цифрами. Знак равенства в приближенных вычислениях имеет другой смысл, чем в алгебре. Равенство означает близость значений. Точность приближенного равенства, т.е. степень близости точного значения А и приближенного а, характеризует абсолютная погрешность, Δ(a) – величина, характеризующая степень близости точного значения A и приближенного a, которая определяется формулой 1.
Δ(a) = |A – a|. (1)
На практике абсолютная погрешность обычно неизвестна, поэтому используют предельную абсолютную погрешность Δ, определяющуюся неравенством 2.
|A – a| ≤ Δ. (2)
Информацию о том, что, а является приближенным значением числа А с абсолютной погрешностью Δ, принято записывать в виде:
A = a ± Δ, (3)
где числа а и Δ записываются с одинаковым количеством знаков после запятой. Например, А = 1.125 ± 0.005, означает, что А находится в интервале: 1.125 - 0.005 < А < 1.125 + 0.005. Таким образом, величине А сопоставляется с интервалом (1.120, 1.130) [1, c. 3].
Более полно характеризует степень точности приближенного числа относительная погрешность, так как позволяет сравнивать точность задания величин, как существенно различающихся по порядку, так и выраженных в разных единицах измерения. Относительная погрешность часто выражается в процентах, обозначается δ(a) и определяется из соотношения, описанного неравенством 4.
|(a – A) / a ≤ δ(a)|. (4)
При сложении двух чисел абсолютная погрешность их суммы будет равняться сумме их абсолютных погрешностей:
Δ(a ± b) = Δ(a) + Δ(b) (5)
При умножении (делении) двух чисел относительная погрешность их произведения (отношения) будет равняться сумме их относительных погрешностей:
δ(a · b) = δ(a) + δ(b). (6)
δ(a / b) = δ(a) + δ(b). (7)
Описание предметной области
В промышленности, где используется создание сплавов из различного количества примесей для регулирования, количества полученного брака существуют контроллеры, которые с определенной периодичностью передают информацию другим контроллерам, которые необходимы для объединения и отправки полученных данных в базу данных. В данном случае необходимо регулировать период времени отправки данных и сам процесс создания сплавов для того, чтобы отследить момент создания брака. Проблема регулирования периодичности сброса информации в базу данных усугубляется тем, что для некоторых процессов периодичность отправки данных составляет часы, а для других миллисекунды. Соответственно, при получении информации о браке, необходимо повторно определять количество примесей в сплаве, а для быстрого увеличения точности можно использовать алгоритм, основанный на клиент-серверных числах. Данный алгоритм позволяет быстро увеличить точность конечного числа, полученного при помощи арифметических операций.
Алгоритм клиент-серверных чисел
Появление клиент-серверных приложений, ориентированных на то, что все основные вычисления производятся на стороне сервера, а на клиентской стороне уже отображается полученные результаты вычислений привело к тому, что данную технологию начали использовать в других процессах. Число клиент – это число, способное повысить свою точность путём отправления запроса на повышение точности своих аргументов чисел-серверов. Число клиент хранит в себе ссылки на свои аргументы, информацию об арифметической операции и полученный результат. Таким образом, клиент-серверные числа можно представить в виде бинарного дерева. Рассмотрим пример, показанный на рисунке 1.
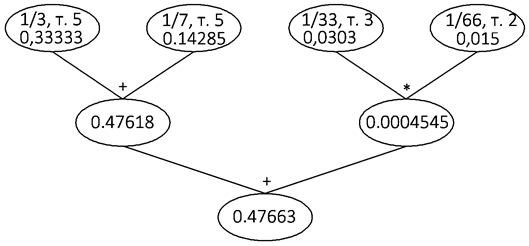
Рис. 1. Клиент-серверные числа, изображенные в виде бинарного дерева
Аргументом нулевого поколения или предком нулевого поколения называется число-клиент, не имеющее аргументов-серверов. Точностью нулевого аргумента является количество значащих цифр десятичной дроби. Поколением числа-сервера является максимальная длина пути от этого числа до его нулевого аргумента. Для повышения точности числа-клиента на n знаков необходимо повысить точность аргументов этого числа таким образом, чтобы у числа, отправившего запрос на повышение, стало на n точных цифр в записи больше. Например, для повышения точности числа 0,47663 из рисунка 1 на 2 знака необходимо повысить точность аргументов, как показано на рисунке 2.
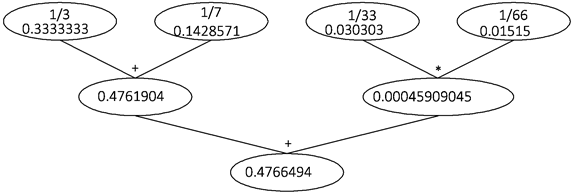
Рис. 2. Повышение точности клиент-серверных чисел
Использование алгоритма клиент-серверных чисел позволяет достигнуть увеличения точности конечного результата алгебраической формулы, составленной из арифметических операций, на неопределенное число знаков. Данное преимущество позволяет не производить перерасчета всех операций для того, чтобы повысить точность конечного числа. При этом при перерасчете может выйти так, что конечная точность числа повысилась на меньшее количество знаков, чем необходимо, поэтому в таком случае придется каждый раз заново производить вычисления всех операций. Проблема усугубляется тем, что операций, которые необходимы для расчета конечной величины может быть сотни, тысячи и более. Данная перспектива приводит к тому, что время, необходимое для получения конечного результата, увеличивается на непредсказуемое число. Поэтому в данном случае, необходимость быстрого перерасчета всех операций является актуальным.
Приложение для использования клиент-серверных чисел
На данный момент нет удобного приложения, которое могло бы использоваться как калькулятор, позволяющий увеличить точность произведенных операций с числами. Поэтому в данный момент ведется разработка приложения на языке Qt C++, которое будет являться кроссплатформенным и позволять регулировать точность, производя быстрый перерасчет за счет алгоритма клиент-серверных чисел.
Подобное приложение может быть полезно при использовании на производстве, например, для корректного регулирования качества получения сплавов или другой продукции.
Разрабатываемое приложение не является нацеленным на использовании в конкретной предметной область, оно также может найти свое применение в различных сферах, нуждающихся в быстром повышении точности конечного результата, полученного совокупностью произведенных арифметических операций.
Заключение
В данной статье рассмотрен алгоритм клиент-серверных чисел, позволяющий управлять точностью чисел с периодичным или бесконечным количеством знаков после запятой, полученных при помощи большой совокупности арифметических операций над числами, которые также имеют бесконечное число знаков после запятой.
Проведен обзор ведущихся на момент написания статьи разработок для обеспечения увеличения качества производимой продукции из сплавов. Данные разработки должны обеспечить промышленность инструментом, позволяющим быстро повысить точность конечного результата.

.png&w=640&q=75)