Определение собственной частоты колебаний упругой оболочки и ее присоединенной массы

Введение. При решении задач динамики, часто возникает необходимость экспериментального определения параметров, входящих в дифференциальные уравнения, которые описывают какую-либо технологическую систему или процесс.

Например, сейчас в России производятся установки для утилизации изношенных покрышек фрезерованием крупногабаритной цилиндрической фрезой [1, 2]. Для одной из таких установок [2] была составлена и опубликована [3] математическая модель, которая в перспективе должна позволить снизить затраты на натурные испытания и доработку. Модель содержит ряд неизвестных параметров, относящихся к обрабатываемому объекту – автомобильной покрышке. Результаты экспериментального определение радиальной и тангенциальной жесткости покрышки ранее уже были опубликованы [4]. В данной статье приводятся результаты экспериментального определения собственной частоты колебаний автомобильной покрышки и ее присоединенной массы, которые могут быть применимы и к другим аналогичным задачам.

Постановка задачи. В случае вынужденных или свободных колебаний упругой оболочки, колебания совершает не вся оболочка, а лишь некоторая ее часть. Массу этой части оболочки далее будем называть присоединенной.

Значение присоединенной массы можно выразить из формулы определения собственной частоты колебаний тела [5, с.79], [6, с.11], [7, с.62]. Получим:

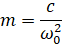
где m – присоединенная масса, кг; c – жесткость, Н/м; ω₀ – собственная круговая частота колебаний, рад/с.

Чтобы воспользоваться этой формулой, необходимо знать собственную частоту колебаний оболочки. При отсутствии внутреннего трения собственная частота совпадает с резонансной. В случае вынужденных гармонических колебаний при наличии трения, резонансную частоту колебаний можно вычислить по формуле [5, с. 101]:

,

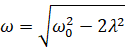где ω – резонансная частота колебаний, рад/с;  λ – коэффициент затухания, с^-1.

При этом, если λ <<ω₀, разница между резонансной частотой и собственной будет второго порядка малости [5, с. 101] и ей можно пренебречь. В этом случае ω=ω₀.

Известно, что явление резонанса, сопровождается значительным ростом амплитуды колебаний. В случае вынужденных колебаний при наличии вязкого трения, величина амплитуды колебаний при резонансе зависит от коэффициента затухания λ  [5, с. 105], [6, с.23] и вычисляется по формуле:

,

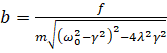где b – амплитуда колебаний, м; ω₀ – собственная круговая частота колебаний, рад/с; γ – частота воздействия вынуждающей силы, рад/с; λ – коэффициент затухания, с^-1; f – амплитуда вынуждающей силы, Н; m – масса, кг.

При достаточно большом значении коэффициента затухания, резонанс может вообще не сопровождаться ростом амплитуды (рис. 1). Также с ростом коэффициента затухания, границы области резонанса становятся более размытыми, а максимум амплитуды сдвигается в область меньшей частоты, относительно собственной. В результате определение области резонанса по амплитуде колебаний для материалов с высоким значением коэффициентом демпфирования, каковым, например, является резина, затруднительно, либо вовсе невозможно.

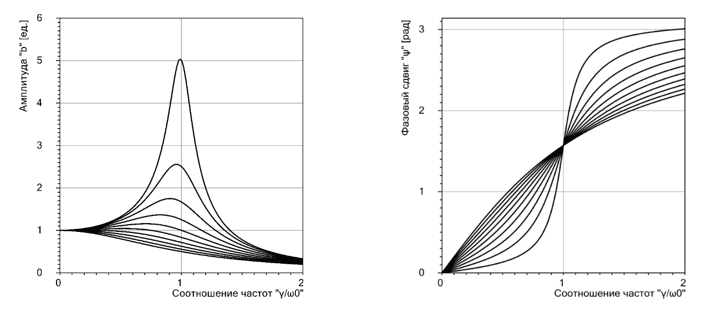
Рис. 1. Графики зависимости амплитуды колебаний b  и фазового сдвига ψ  от λ  и отношения частоты вынуждающей γ  к собственной частоте колебаний ω₀. Для верхней линии λ=0,1ω₀, для нижней λ=1ω₀, шаг промежуточных линий 0,1ω₀

Известна другая характерная особенность вынужденных колебаний – разность фаз ψ между перемещением колеблющегося тела и вынуждающей силой при совпадении частот равна  [5, с. 104], [6, с.21] и не зависит от значения коэффициента демпфирования (рис. 1). Таким образом, зная фазовый сдвиг ψ между вынуждающей силой и смещением поверхности оболочки в точке приложения этой силы при изменении частоты колебаний, можно достаточно точно определить собственную частоту колебаний.

Для экспериментального определения частоты собственных колебаний автомобильной покрышки этим методом, была сконструирована специальная установка, показанная на рис. 2.

Рис. 2. Установка определения резонансной частоты колебаний покрышки

На массивном металлическом столе надежно закреплена покрышка. Рядом с покрышкой на стол устанавливается вибратор. Вибратор воздействует на протектор покрышки через толкатель 6, к которому жестко присоединен высокоточный тензометрический датчик давления с линейной зависимостью. Толкатель 6 соединен с электромотором 1 через кривошипно-шатунный механизм 4 и ременную передачу 2. Электромотор 1 представляет собой асинхронный трехфазный двигатель АПН 011/4, с частотой вращения вала n_дв=1390 об/мин и мощностью 50 Вт. Передаточное отношение ременной передачи 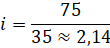. Частота вращение вала электромотора регулируется с использованием частотного регулятора ОВЕН ПЧВ 101-К37А. Кривошип выполнен в виде эксцентрикового механизма, что позволяет плавно регулировать амплитуду колебаний толкателя от 0 до 3 мм. Вал кривошипно-шатунного механизма закреплен в подшипниковой опоре 3. Датчик 7 представляет собой оптопару. Совместное использование датчика 7 с диском 8, имеющим небольшую прорезь у края, позволяет фиксировать «нулевое» положение толкателя 6, при котором вынуждающая сила равна нулю.

Для проведения эксперимента использовалось следующее измерительное оборудование: сейсмический вибродатчик измерения вибросторости СГ-10, осциллограф С1-93, низкочастотный звуковой генератор ГЗ-102, оптопара, высокоточный керамический тензодатчик давления, легковая покрышка MATADOR-OMSKSHINA MP-50 Sibir массой 6,9 кг.

В ходе эксперимента, на осциллограф С1-93 подавались сигналы: на ось Oy с вибродатчика виброскорости СГ-10, на ось Ox со звукового генератора ГЗ-102. Вибродатчик виброскорости СГ-10 плотно прижимался к протектору колеблющейся покрышки. Далее выполнялось изменение частоты сигнала звукового генератора до появления на экране осциллографа фигур Лиссажу. Таким образом, по частоте звукового генератора определялась текущая частота колебаний покрышки.

Максимальная частота колебаний, достигнутая с использованием данной установки, составила ξ_max Гц. Звуковой генератор ГЗ-102 выдает частоты от 17,7 до 210 Гц, без использования множителя. Таким образом, диапазон частот, которые можно точно определить и зафиксировать с использованием звукового генератора и данной установки составляет 17,7÷46 Гц.

В результате выполнения эксперимента по определению собственной частоты колебаний покрышки с использованием виброустановки были получен ряд графиков, показанных на рис. 3 и 4.

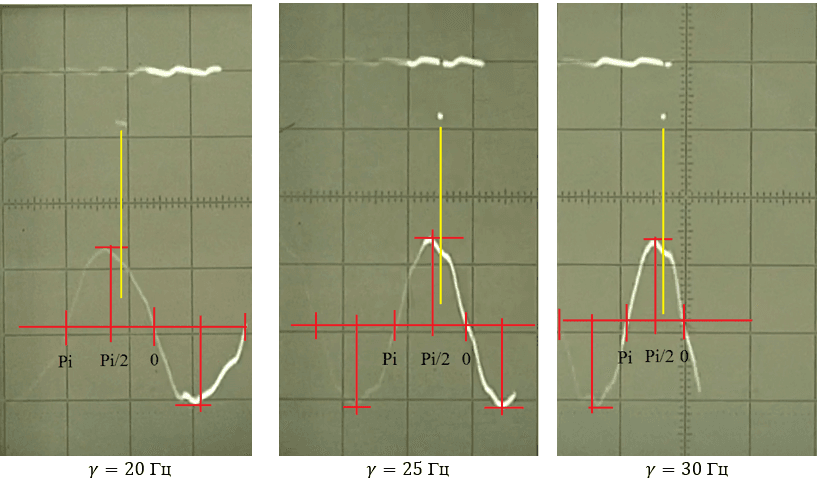
Рис. 3. Фазовый сдвиг между вынуждающей силой и перемещением

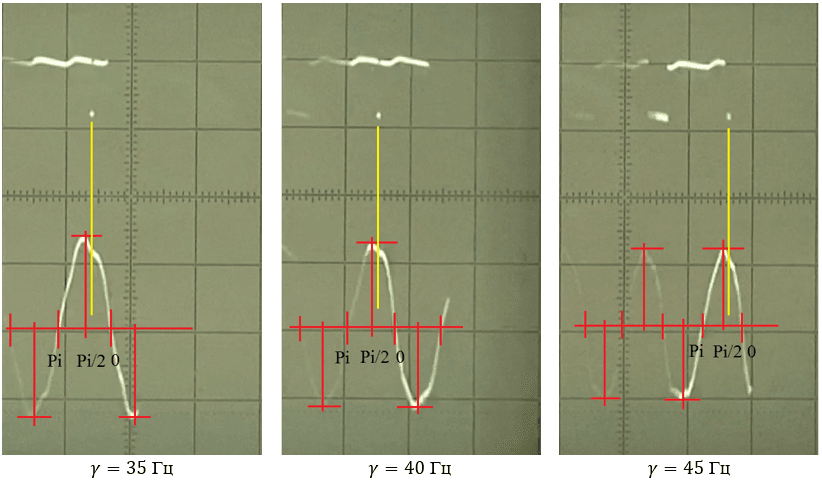
Рис. 4. Фазовый сдвиг между вынуждающей силой и перемещением

Длинная вертикальная линия показывает фазовый сдвиг «нулевой» точки относительно вынуждающей силы. Значение фазового сдвига при этом составило приблизительно 67°. Видно, что независимо от частоты колебаний эта линия остается почти неподвижной. Такой результат является довольно странным, поскольку с ростом частоты она должна приближаться к линии Pi/2. Поэтому был выполнен еще ряд экспериментов.

Для приближенного определения форм и частот собственных колебаний шины, была построена упрощенная трехмерная модель шины в программе SolidWorks. Материал шины – резина, со следующими характеристиками: модуль Юнга E=15 МПа, модуль упругости при сдвиге G=3 МПа, коэффициент Пуассона μ=0,49, плотность ρ=1100 кг/м3. Наличие корда в шине не учитывалось.

Далее, в SolidWorks Simulation были определены собственные формы и частоты свободных колебаний этой модели шины. В результате были получены 5 форм (табл.) и собственных частот колебаний. Однако две из пяти формы колебаний являются ортогональными двум другим (частоты колебаний идентичны). Таким образом, были получены лишь 3 действительно отличных друг от друга формы и частоты колебаний. Модель шины была жестко зафиксирована за бортовые кольца.

Таблица

Формы и собственные частоты колебаний модели покрышки

Эксперимент по определению собственной частоты колебаний методом свободного удара дал результаты, которые хорошо согласовываются с расчетами, выполненными в SolidWorks Simulation.

Данным методом возможно экспериментальное определение низших резонансных частот путем замера частоты свободных колебаний исследуемого объекта после удара. Найденная таким методом частота колебаний будет меньше частоты собственных колебаний в отсутствии трения. Однако влияние трения на частоту свободных колебаний значительно меньше, чем влияние на амплитуду, в связи с чем, даже при достаточно большом коэффициенте затухания можно принять эти частоты равными [6, с.12].

При выполнении этого эксперимента использовалось следующее оборудование: сейсмический вибродатчик измерения вибросторости СГ-10, осциллограф С1-93, низкочастотный звуковой генератор ГЗ-102, молоток.

К протектору покрышки прижимался датчик измерения виброскорости и наносился удар молотком в трех местах: рядом с датчиком, под углом в 90° к оси датчика, а также с противоположной стороны (180°). Показания осциллографа записывались на видеокамеру. Результаты приведены на рис. 5.

Рис. 5. График изменения виброскорости при свободном ударе (1дел.–30 мс)

Также в результате хаотично направленных постукиваний, был получен график изменения виброскорости наиболее близкий к гармоническому (рис. 6). Видно, что одно колебание происходит за 15 мс. Таким образом, частота собственных колебаний данной покрышки составляет 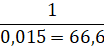 Гц.

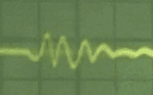
Рис. 6. График изменения виброскорости при свободном ударе (1дел. – 30мс)

Используя данные графики виброскорости можно приближенно вычислить коэффициент затухания λ, по времени τ уменьшения амплитуды колебаний в e раз, с использованием формулы:

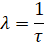
Эта формула связана с амплитудой колебаний, которая при проведении экспериментов не измерялась. Однако, через 100 мс виброскорость падает практически до нуля, а значит и амплитуда, уменьшается более чем в e раз и с некоторой погрешностью можно определить d  и λ. Полученная таким образом λ будет меньше реальной.

Получаем:

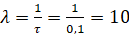 с^-1

С использованием λ=10 с^-1 можно построить расчетный график фазового сдвига, аналогичный рис. 1.

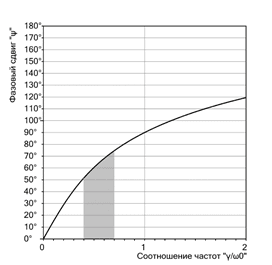
Рис. 7. Фазовый сдвиг ψ  при λ=10 с^-1 и ω₀=66,6 Гц.

На рис. 7 серым цветом выделена область, в которой проводилось экспериментальное определение фазового сдвига. Экспериментальное значение фазового сдвига составило 67°. Как видно из графика это значение попадает в выделенную область. Таким образом, можно сделать вывод, что измеренное значение фазового сдвига верное, а его почти неизменное значение можно объяснить отклонением от линейности свойств материала, погрешностью измерений и высоким значением коэффициента затухания, при котором колебания также становятся нелинейными.

Зная собственную частоту колебаний шины ω₀  и ее радиальную жесткость c , которая уже была определена ранее [4], можно вычислить значение присоединенной массы:

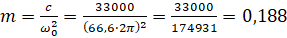кг.

Таким образом значение присоединенной массы составляет почти 200 грамм или около 3% массы всей покрышки. Однако на самом деле значение присоединенной массы также зависит от частоты вынужденных колебаний и амплитуды, поскольку жесткость покрышки нелинейная [4].

Заключение. В результате определена собственная частота колебаний покрышки, найдено значение ее присоединенной массы, а также найдено приближенное значение коэффициента затухания. Также можно заключить, что метод свободного удара оказался точнее метода фазового сдвига и проще в постановке.