Начиная с версии 15, в программе MathCAD появилась возможность вычислять эллиптические интегралы, что позволяет решать задачи, содержащие эти интегралы, не прибегая методам, изложенным в [2]. При этом возникают некоторые особенности применения программы, которые рассмотрим на примере задачи расчета большого изгиба упругого стержня, приведенной в [1, с. 111], рис. 1.
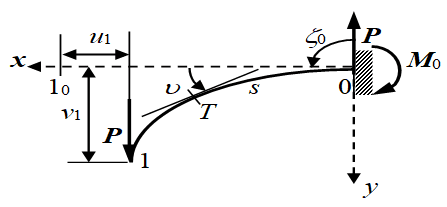
Рис. 1
Все обозначения и формулы взяты из [1].
Расчет в программе MathCAD целесообразно начать с задания значений модулярного угла 0 ≤ a < 900. При этом значение угла a = 900 следует избежать, так как при этом значение полного эллиптического интеграла F(k) = ∞, а для сохранения количества расчетных значений уменьшить шаг изменения угла a. Например, приняв ранжированную переменную i = 1…12, задаем значения угла ai = 41deg + 4deg·i и последовательно вычисляем модуль k, интегралы F(k), E(k), F(j0), E(j0), параметр j0, коэффициенты подобия b и w0 по формулам: ki = sinai ;
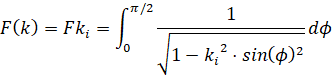 - полный эллиптический интеграл 1-го рода;
- полный эллиптический интеграл 1-го рода; 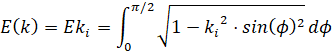 полный эллиптический интеграл 2-го рода; где z0 = p/2 – угловой коэффициент подобия;
полный эллиптический интеграл 2-го рода; где z0 = p/2 – угловой коэффициент подобия;
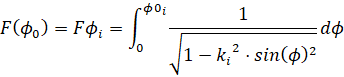 - эллиптический интеграл 1-го рода;
- эллиптический интеграл 1-го рода;
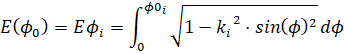 - эллиптический интеграл 2-го рода;
- эллиптический интеграл 2-го рода;
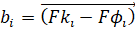 - коэффициент подобия. Особенностью здесь является то, что в последующих формулах возникает ошибка «деление на ноль». В этой связи значение bi следует переопределить так: b1i = bi – 10-10, что не отражается на значениях bi, вычисляемых обычно до 3-4 знака после запятой.
- коэффициент подобия. Особенностью здесь является то, что в последующих формулах возникает ошибка «деление на ноль». В этой связи значение bi следует переопределить так: b1i = bi – 10-10, что не отражается на значениях bi, вычисляемых обычно до 3-4 знака после запятой.
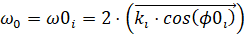 - параметр, связанный с моментом в точке 0 заделки балки (см. ниже). Вычисленные значения сведены в таблицу 1.
- параметр, связанный с моментом в точке 0 заделки балки (см. ниже). Вычисленные значения сведены в таблицу 1.
Таблица 1
|
a0 | 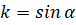 |
F(k) |
E(k) |
j00 |
F(j0) |
E(j0) |
b |
w0 |
|---|---|---|---|---|---|---|---|---|
|
45 49 53 57 61 65 69 73 77 81 85 89 |
0,707 0,755 0,799 0,839 0,875 0,906 0,934 0,956 0,974 0,988 0,996 1,000 |
1,854 1,918 1,993 2,080 2,184 2,309 2,461 2,652 2,903 3,255 3,832 5,435 |
1,351 1,315 1,278 1,240 1,202 1,164 1,127 1,093 1,061 1,034 1,013 1,001 |
90,000 69,542 62,300 57,472 53,947 51,279 49,237 47,682 46,528 45,719 45,219 45,009 |
1,854 1,388 1,234 1,134 1,062 1,008 0,967 0,935 0,912 0,896 0,886 0,882 |
1,351 1,074 0,969 0,897 0,844 0,803 0,772 0,748 0,731 0,718 0,710 0,707 |
0,000 0,503 0,738 0,946 1,122 1,301 1,494 1,717 1,991 2,360 2,946 4,553 |
0,000 0,528 0,742 0,902 1,029 1,134 1.219 1.288 1.341 1,379 1,403 1,414 |
По полученным значениям величин определяются все геометрические и силовые параметры изогнутого гибкого стержня.
1. Траектория концевой точки 1 стержня подсчитывается по формулам:
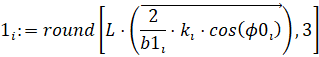 ,
, 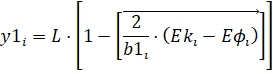 ,
,
где L – длина стержня. Примем L = 10 см. Однако при подсчете по приведенным формулам первые значения существенно отличаются от вторых: 0,000 – 9,948 и 10,000 – 0,929 соответственно, что приводит к появлению лишней линии на графике. Поэтому первую точку следует исключить оператором submatrix:
x2 = submatrix(x1, 2, 12, 1, 1), y2 = submatrix(y1, 2, 12, 1, 1).
Траектория концевой точки 1 показана на рис. 2. Полученные значения координат х2 и у2 приведены в таблице.
|
№ |
х2 см. |
у2 см. |
|
1 2 3 4 5 6 7 8 9 10 11 |
9,948 9,793 9,534 9,175 8,716 8,158 7,500 6,736 5,845 4,164 3,105 |
0,929 1,849 2,759 3,620 4,455 5,246 5,988 6,679 7,325 7,948 8,711 |
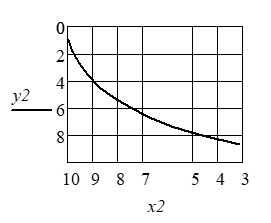
Рис. 2
2. Прогибы стержня: горизонтальный u = L – x2, вертикальный v = y2.
3. Угол наклона касательной в концевой точке 1 к оси х:
u1 = z1 - p / 2, где 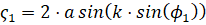 (arcsin в MathCAD – asin).
(arcsin в MathCAD – asin).
z10 =
|
1 2 3 4 5 6 7 8 9 10 11 12 |
|
90 98 106 114 122 130 138 146 154 162 170 178 |
u10 =
|
1 2 3 4 5 6 7 8 9 10 11 12 |
|
0 8 16 24 32 40 48 56 64 72 80 88 |
4. Зависимость силы от вертикального прогиба стержня (статическая характеристика). Примем жесткость стержня Н = 104 Нсм2, длину стержня L = 10 см. Сила подсчитывается по формуле
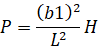 Н.
Н.
|
№ |
1 2 3 4 5 6 |
|
Р Н |
28,126 57,488 89,487 125,901 169,230 223,331 |
|
№ |
7 8 9 10 11 |
|
Р Н |
294,780 396,228 556,735 867,877 2,073·103 |
Число значений Р следует согласовать с числом значений у2, устранив первое значение операцией P1 := submatrix(P, 2, 12, 1, 1). График зависимости Р1 = Р1(у2) приведен на рис.3.
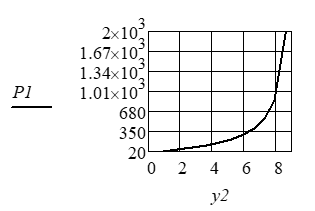
Рис. 3
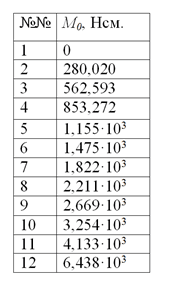
5. Изгибающий момент в заделке:
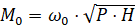 Нсм. (Р0 = 0).
Нсм. (Р0 = 0).
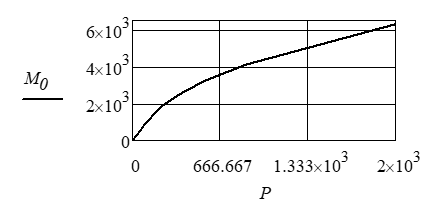
Рис. 4
Зависимость М0 = М0(Р) приведена на рис. 4
6. Наибольшее напряжение в заделке. Примем поперечное сечение стержня в виде прямоугольника с толщиной h = 0,2 см, модуль упругости
Е = 2,1·107 Н/см2 (сталь углеродистая), длину стержня L = 10см. Наибольшее напряжение в заделке вычисляется по формуле
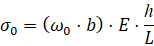 Н/см2.
Н/см2.
s0 =
|
1 2 3 4 5 6 7 |
|
0 5,88·104 1,181·105 1,792·105 2,425·105 3,098·105 3,826·105 |
|
8 9 10 11 12 |
|
4,644·105 5,606·105 6,833·105 8,680·105 1,352·106 |
7. Зависимость силы от длины стержня. Примем жесткость стержня
Н = 104 Нсм2. Длину стержня зададим в виде ранжированной переменной Lj = 4,5 + 0,5·j см. Значения сил для заданных значений L вычисляем по формуле
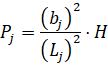 Н. Получим
Н. Получим
|
L, см. |
5,0 5,5 6,0 6,5 7,0 7,5 8,0 8,5 |
|
Р, Н |
0 92,972 159,690 211,804 256,841 0,021 300,853 349,955 |
|
L, см. |
8,5 9,0 9,5 10,0 10,5 |
|
Р, Н |
408,000 489,170 616,880 867,877 1,881·103 |
Зависимость Р = Р(L) приведена на рис. 5.
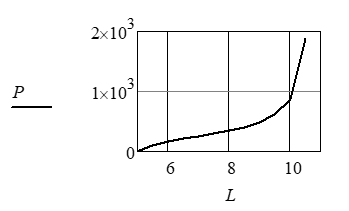
Рис. 5
|
1 2 3 4 5 6 7 8 9 10 11 12 |
0 13,009 52,186 118,007 211,377 333,840 788,022 678,596 914,676 1,217·103 1,649·103 2,660·103 |
8. Внутренняя энергия изгиба подсчитывается по формуле
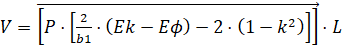 Нсм.
Нсм.
Значения внутренней энергии стержня приведены в таблице справа.
9. Уравнение упругой линии. Построим упругую линию для значений b = 1,122, k = 0,875, a = arcsin(k) = 610, L = 10 см. По приведенной выше таблице или формуле определяем j0 = 0,942 рад. (= 53,9470). Вычислим эллиптические интегралы (или возьмем из таблицы):
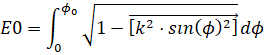 , Е0 = 0,844, F0 = 1,062.
, Е0 = 0,844, F0 = 1,062.
Задав ранжированную переменную j = 1 ..11, определим дуговую координату sj = (L/10)·(j – 1). Вычислим значение интеграла Fj по формуле:
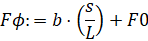 .
.
По значениям Fj определяем амплитуду j , используя таблицу 1 в [2, с. 322].
|
№ |
Fj |
j1 рад |
|---|---|---|
|
1 2 3 4 5 6 7 8 9 10 11 |
1,062 1,174 1,286 1,399 1,511 1,623 1,735 1,847 1,960 2,072 2,174 |
0,942 1,018 1,091 1,160 1,226 1,288 1,348 1,405 1,461 1,516
|
При этом значения Fj и соответственно j могут не совпадать с табличными. Тогда прибегаем к линейной интерполяции по формуле
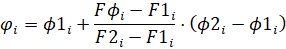 ,
,
где F1 и F2 ближайшие меньшее и большее значения к Fj , j1 и j2 – значения аргумента, соответствующие F1 и F2. При этом число значений f уменьшится на единицу.
Текущие координаты упругой линии х и у вычисляются по формулам:
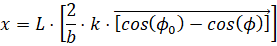 см.;
см.;
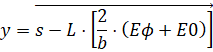 см.
см.
Значения интеграла Еj определяют по формуле 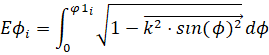 , а значения дуговой координаты s уменьшают на единицу для согласования с числом значений Еj : s1 = submatrix(s, 10, 1, 1). График упругой линии приведен на рис. 6.
, а значения дуговой координаты s уменьшают на единицу для согласования с числом значений Еj : s1 = submatrix(s, 10, 1, 1). График упругой линии приведен на рис. 6.
Силу, отвечающую данному изгибу упругой линии, определяют по формуле P:= (b2 / L2)·H (H). Так, при b = 1,122, L = 10 см. и Н = 104 Нсм2 получаем Р = 125,888 Н.
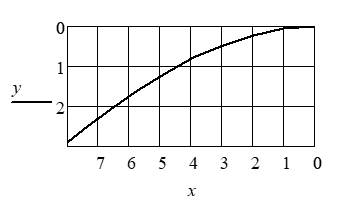
Рис. 6
Аналогично строят графики и для других значений задаваемых величин.

.png&w=640&q=75)