GİRİŞ. Tədqiqatda strategiya oyunlarının kompüter mühitində tədqiqinə baxılmışdır. Əsasən tədqiqatda şirkətlərin bir oyun proqramını istehsal edərkən hansı mərhələlərdən keçdikləri və oyunlar nəzəriyyəsi haqqında məlumatlar yer almışdır. Praktiki hissə üçün unity oyun düzəltmə motorundan, proqramlaşdırma dili olaraq c# dilindən istifadə edərək şahmat oyunu düzəldilmişdir. Bu praktiki hissədə proqramlaşdırma, süni intellekt və şəbəkə sahələrini özündə birləşdirmişdir.
TƏDQİQAT METODU. Oyunlar nəzəriyyəsi - tərəflərin strateji qarşılıqlı fəaliyyətini təhlil etmək üçün riyazi sxemdir. O maraqların münaqişəsi şərtləri zəminində fərdlərin rasional davranışının məntiqini izah etməyə kömək edir.
Oyunlar nəzəriyyəsinin yaranması ümumiyyətlə 1944-cü ildə Jon fon Neymann və Oskar Morgenstern "Oyun nəzəriyyəsi və iqtisadi davranış" monoqrafiyasının nəşri ilə əlaqələndirilir. Yarandığı gündən bəri oyunlar nəzəriyyəsinin əsas tətbiq sahələri hərbi-strateji və beynəlxalq məsələlər olmuşdur.
1950-ci illərdə oyun nəzəriyyəsi ilə və onun hərbi-strateji sahədə tətbiqi ilə bağlı klassik əsərlər nəşr olundu. Oyunlar nəzəriyyəsinin tətbiq sahələri genişlənirdi.
Qeyd etmək lazımdır ki, R. Lews və H.Rifın 1944-cü ildə dərc olunmuş klassik monoqrafiyasında ilk növbədə sıfır cəmli oyunlara və kooperativ oyunlara diqqət yetirilmişdi. Sıfır cəmli oyunlar - bir tərəfin qazancı digər tərəfin itkisinə bərabər olan oyunlardır. İki oyunçunun iştirak etdiyi sıfır cəmli oyunlara antaqonist oyunlar deyilir. Əslində sıfır cəmli oyunlara daha geniş bir sinif oyunları aid edilə bilər-sabit cəmli oyun, burada bütün oyunçuların ümumi uduş cəmi sabit olduğu və bu səbəbdən onlardan birinin uduşunda artım yalnız digər tərəfin uduşunun azalması ilə mümkündür.
Sıfır cəmli oyunlar təmiz qarşıdurma vəziyyətlərini təsvir edir, yəni iştirakçıların əks maraqları var (idman, hərbi münaqişələr). Oyunçuların sayı ikidən çox olduğu sıfır cəmli oyunlarda bəzi oyunçuların qalan oyunçular hesabına orta qazanclarını artırması üçün onlar arasında koalisiyalar qurma ehtimalını nəzərə almaq lazımdır.
Oyunlar Nəzəriyyəsi, əsas olaraq iki teorem üstünə qurulmuşdur. Bunlardan birincisini, yəni “min-max teoremi” adı ilə bilinən teoremdir, hansı ki keçən əsrin riyaziyyatçısı Jon Fon Neyman irəli sürmüşdür. İkincisi və çox daha əhəmiyyətlisini isə Naş irəli sürmüşdür. Buna da 'Naş Tarazlığı' deyilir. “Naş tarazlığı” ilə əlaqədar teorem dərhal dövrün ən yaxşı beyinləri tərəfindən test edildi. Bu testlərdən biri üçün inkişaf etdirilən oyunlardan biri “Dustaqların Dilemması” idi. Bu oyunu, Naşın doktor müəllimi Al Tucker icad etmişdi.
'Naş Tarazlığı' iki və ya daha çox oyunçuların iştirak etdikləri qeyri-koperativ oyunlar üçün həll konseptidir. Bu konseptdə bunlar fərz olunur ki, hər bir oyunçu digər hər bir oyunçunun tarazlıq strategiyasını bilir və heç bir oyunçu yalnız öz strategiyasını dəyişməklə öz qazancını artıra bilməz. Əgər bütün oyunçular öz strategiyalarını seçmişlərsə və heç bir oyunçu yalnız öz strategiyasını dəyişməklə artıq heç bir qazanc əldə edə bilmirsə, onda bu strategiyalar seçimi və müvafiq qazanclar (mükafatlar) Naş tarazlığını təşkil edir
“Min-max teoremi” adı ilə bilinən teoremi əsas tutaraq Unity oyun və ya proqram düzəltmə platformasından istifadə edərək şahmat oyunu yaradılmışdır. Bu oyunu tərtib etmək üçün C# proqramlaşdırma dilinin resurslarından istıfadə olunub. Süni intellekt hissəsini yaratmaq üşün minimax algoritmindən istifadə edilmşdir.
Oyunlarda itkini minumuma endirmək üçün istifadə olunan bir metoddur. Kompüterin Təsadüfi oynamaq yerinə sonrakı hərəkəti hesablayaraq daha uyğun oynamağa kömək edən bir alqoritmdir. Əsasən dama, şahmat, tictactoe kimi oyunlarda istifadə olunan bir alqoritmdir. Kompüterlə oynamaq üçün süni intellekt yaratmaq lazım gəlir. Bunu daha yaxşı variantda yaratmaq üçün neyron şəbəkələrdən istifadə eləmək olar. Amma məqsədə uyğunu Minimax algoritmindən istifadə etməkdir. Bunun üçün əvvəlcə bütün mümkün olan hallar toplanılır, bundan sonra təsadüfi olaraq seçilmiş bir halı kompüter yerinə yetirir.
Minimax, digər oyunçunun da yaxşı oynadığını fərz edərək bir oyunçu üçün ən yaxşı hərəkəti seçmək üçün istifadə olunan rekursiv bir alqoritmdir. MIN və MAX adlı oyunda iki hissə var. MAX hissə mümkün olan ən yüksək, MIN isə mümkün olan ən aşağı bal toplamağa çalışır, yəni MIN və MAX bir-birinin əksinə hərəkət etməyə çalışır.
İndi isə Minimax algoritmini yazaq. Bunun üçün hər bir fiqura bir dəyər veririk: piyada-1, at-2, fil-3, qala-5, vəzir-9. Ən vacib fiqurumuz şah olduğu üçün ona ən yüksək qiymətlə, məsələn 100 dəyərləndiririk. Sonra hər bir xanaya hər bir fiqura görə dəyər veririk, bu isə o deməkdir ki, bu fiqurlar yerləşdiyi xanaya necə təsir edir. Verdiyimiz dəyərlərə əsasən algoritm bizə ən yaxşı nəticəni verəcək. Rəqibimiz də ən yaxşı nəticəni seçərək oyunu oynayacaq. Bunu nəzərə alaraq ehtimalları göz qabağında tutaraq bu alqoritm vasitəsilə 2-3 gediş üçün bunu hesablaya bilərik. Bunu aşağıdakı kimi ağac formasında göstərə bilərik.
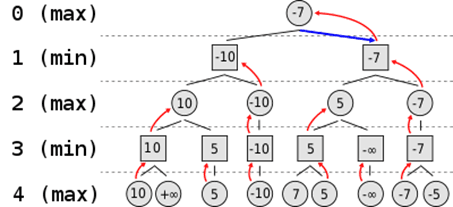
Şəkil 1. Minimaxın ağac formasında görünüşü
Alqoritm rəqibin ən yaxşı nəticəsini nəzərə alaraq bir ümumi nəticə bizə verir. Məsələn yuxarıda da göstərildiyi kimi ağacın yuxarıdan aşağıya doğru bizim qeyd etdiyimiz gediş qədər bütün ehtimallara baxır. Daha sonra bu alınan sonuncu nəticənin bizim oyunumuza necə təsir edəcəyini bilmək üçün bir dəyər qeyd edir. Bu dəyər fiqurların dəyərindən və fiqurların xanaya necə təsir göstərməsindən asılıdır. İkinci hissədə isə bu alınan bütün ehtimallar içindən ən yaxşı nəticəni hesablaya bilmək üçün aşağıdan yuxarıya doğru getmək lazımdır. Bunu alqoritm birinci rəqibin ən yaxşı nəticəsini nəzərə alaraq ən kiçik dəyəri yuxarıya daşıyacaq. Sonra bizim gedişimiz olduğu üçün bu alınan dəyərlərdən ən yüksək dəyər nəzərə alınacaq. Bu proses sona kimi bu formada hərəkət edərək bizə ən yaxşı nəticəni verəcək.
Əgər 3 gedişdən daha çox gedişi bu alqoritmlə hesablaya biliriksə onda daha ən yaxşı nəticəni ala biləcəyik. Bu təbii ki, alqoritmin daha çox işləməsi deməkdi və kompüterin hesablama vaxtı artır ki, buda bizə daha çox gözləməyə gəlib çıxardır.
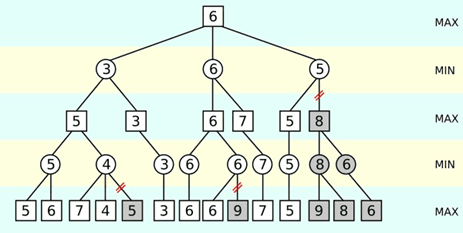
Şəkil 2. Alpha-beta budaması
Minimax yuxarıdan aşağıya gəldikdə sol tərəfi birinci hesablayır sonra, o biri budaqlara baxmadan üst tərəfə bu dəyəri yazır. Sonra sağdakı budaqlara baxaraq hesablayır min hissəsi üçün əgər üst nöqtədəki dəyər sağ tərəfdəki dəyərlərdən kiçikdirsə onda üst nöqtədəkimiz dəyər dəyişmir. Yox əgər böyükdürsə onda üst tərəfin qiyməti sağ tərəfdəki dəyəri alacaq. Bu max hissəsi üçün də eyni cür olacaq.
Alpha-beta budaması istifadə etdikdə bəzi budaqlara baxmağa ehtiyac olmur. Yuxarıda da göstərilən nümunədə də bu göstərilmişdir. Şəkildəki nümunəni nəzərə alaraq izah etməli olsaq, nəyə görə 5 yazılan budaq hesablanmayıb deyə bilərik. Sonuncu sətrdə yalnız kiçik olanlar üstdəki nöqtələrə keçə bilər. İndi birinci sol hissədən başlayacağımız üçün bu budaqdan bizə 5 dəyəri üst nöqtəyə keçəcəkdir. Sağ budağa baxdığımız zaman budağın birinci qiyməti 7, ikinci qiyməti isə 4dür. Sağ tərəfin üçüncü budağını hesablamağa ehtiyac yoxdur, səbəbi isə 4-dən nə qədər kiçik olduğu üçün, sağ tərəfin üçüncü budağını hesablamağa ehtiyac qalmır. Bununla da alpha-beta budaması alqoritmi vasitəsi ilə sürətimiz artmış olur. Təbii ki ən pis halda yenə minimax qədər sürəti olacaq. Əgər təsadüfi olaraq sol tərəfə bizə lazım olan dəyərlər qeyd olunarsa. O zaman alpha-beta budaması alqoritmasının işləyərək kompüterin hesablama sürətinə təsir göstərəcəkdir.
Şəkil 3. Oyun taxtasının xanalarında ağ qala fiqurunun təsiri
NƏTİCƏ. Nəticə olaraq, bildirmək istəyirəm ki, minimaxın strategiya oyunlarına tətbiqi rəqibin gedişlərini əvvəlcədən müəyyən edib ona uyğun olaraq ən yaxşı gedişi etməkdir. Bu alqoritm vasitəsilə kompüterin oynadığı gedişlər daha məntiqli olur.
***
OYUNLARDA İTKİNİ MİNUMUMA ENDİRMƏK ÜÇÜN MİNİMAX TEOREMİNİN TƏTBİQİ İLƏ TƏKLİF OLUNAN METOD
Məqalədə oyunlar nəzəriyyəsi tarixi və bəzi tarixi alimlərin verdiyi nəzəriyyələr haqqında məlumatlar qeyd olunmuşdur. Oyunlar nəzəriyyəsinin hansı sahələrdə istifadə olunduğu göstərilmişdir. Naş Tarazlığı və minimax alqoritmi haqqında məlumatlar və bu nəzəriyyələrin sadəcə oyunlarda deyil başqa sahələrdə də necə işləndiklərinə uyğun misallar bu məqalədə qeyd olunmuşdur. Naş tarazlığı iqtisadiyyatda, rəqib şirkətlər arasında və başqa sahələrdə də işlədilən bir tarazlıqdır. Minimax, digər oyunçunun da yaxşı oynadığını fərz edərək bir oyunçu üçün ən yaxşı hərəkəti seçmək üçün istifadə olunan rekursiv bir alqoritmdir. Əsasən şahmat, poker, dama və s. kimi oyunlarda işlənilə bilən bir alqoritmdir. Məqalədə praktika hissə üçün yaratdığımız şahmat oyununda minimax alqoritminin necə işlədiyi və bu alqoritmdən necə fayda gördüyümüz bu məqalədə göstərilmişdir.
Açar sözlər: oyun nəzəriyəsi, minimax alqoritmi, Naş tarazlığı, alpha-beta budaması.
***
ПРЕДЛАГАЕМЫЙ МЕТОД МИНИМИЗАЦИИ УБЫТКОВ В ИГРАХ С ПОМОЩЬЮ ТЕОРЕМЫ МИНИМАКС
В статье приводятся сведения об истории теории игр и теории данных некоторыми историческими учеными. Показаны области, в которых используется теория игр. В этой статье представлена информация о равновесии Нэша и минимаксном алгоритме, а также приведены примеры развития этих теорий не только в играх, но и в других областях. Равновесие Нэша баланс, используемый в экономике, между конкурирующими компаниями и в других областях. Minimax – это рекурсивный алгоритм, используемый для выбора лучшего хода для игрока, предполагая, что другой игрок сделает свой лучший ход. Этот алгоритм используется в основном в шахматы, покер, шашки и т.д. В этой статье показано, как минимаксное алгоритм работает в шахматной игре, которую мы создали для практической части и как мы извлечь выгоду из этого алгоритма.
Ключевые слова: теория игр, минимаксный алгоритм, равновесие по Нэшу, альфа-бета отсечение.

.png&w=640&q=75)