О биениях музыкальных интервалов

1. Физика частоты колебаний

В фортепиано, скрипке и других музыкальных инструментах звук возникает в результате колебания струн. Музыкальный (чистый) тон – это синусоидальное колебание (рис. 1).

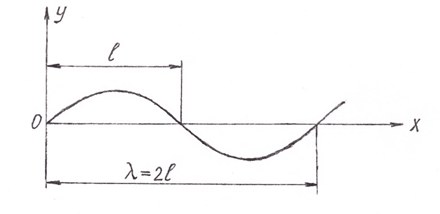
Рис. 1. Синусоидальная волна

Частота f, с которой колеблется каждая частица в волне

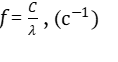 (1)

где с – скорость поперечных волн в струнах,

λ – длина волны или расстояние между частицами, колеблющимися с одинаковой фазой.

Концы каждой струны закреплены, поэтому длина струны равна l.Так как полное колебание состоит из двух синусоидальных полуволн, то

λ=2l.      (2)

Для упругих поперечных волн в струнах, относящихся к твёрдым телам, скорость

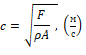 (3)

где F – сила натяжения струны, H,

ρ – плотность материала струны, кг/м³,

A – площадь поперечного сечения струны, м².

С учётом формул (2) и (3) частота колебаний (формула (1)) примет вид:

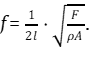  (4)

Приведённые формулы (1-4) взяты из источника [3].

Для отдельно взятой струны все величины, входящие в формулу (4), являются постоянными, поэтому частота f имеет вполне определённое значение.

2. Звук и совокупность гармоник

Как известно, струна звучит при отклонении от прямолинейного состояния до полуволны синусоиды. Если на длине l расположена одна полуволна с амплитудой a₁ (рис. 2, a), то извлекаемый звук называется основным тоном или первой гармоникой.

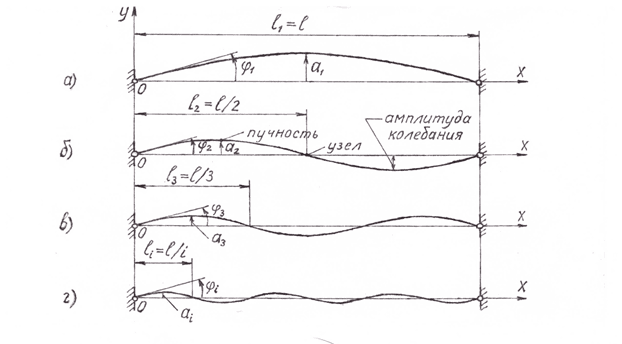
Рис. 2. Гармоники

Если на длине l расположены две полуволны (рис. 2, б) с амплитудами а₂, то этот звук, издаваемый каждой половиной струны, называется первым обертоном, или по-другому, второй гармоникой. Амплитуда замеряется в точке, называемой пучностью. Следующий случай с тремя полуволнами и амплитудами а₃ (рис. 2, в) соответствует второму обертону или третьей гармонике и т. д. до i-й гармоники (рис. 2, г). Длина полуволны i – й гармоники l_i = l/i.

Учитывая, что все обертоны принадлежат одной звучащей струне, углы наклона касательных, проведённых к синусоиде в начале координат 0 осей x, y, будут одинаковыми.

Уравнение синусоиды, записанное для любой гармоники, имеет вид:

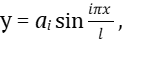 (5)

где i – номер гармоники.

Тангенс угла наклона φ_i касательной к синусоиде равен производной уравнения (5). Эта производная [2] имеет вид:

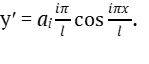   (6)

Найдём амплитуду колебаний a_i из условия равенства углов φ₁ и φ_i или, иначе говоря, из условия равенства угловых коэффициентов y₁ʹ и y_iʹ в начале координат, где х = 0. Это условие имеет вид:

y₁ʹ(х=0) = y_iʹ(x=0).  (7)

Применим условие (7) к уравнению (6).

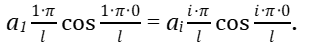
Решаем полученное уравнение.

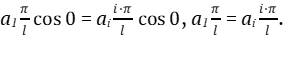
Отсюда

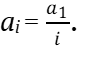  (8)

Громкость звука зависит от величины амплитуды a_i полуволны синусоиды. Как видно из уравнения (8) и рисунка 2 с ростом гармоник (i) амплитуда a_i и, следовательно, громкость звука уменьшаются.

3. Пифагорова комма

Древнегреческий философ и математик Пифагор при настройке музыкальных инструментов применял чистые кварты и чистые квинты.

При последовательном соединении чистой кварты и чистой квинты получается чистая октава. Например: A – d, d – a. Однако, другие ступени октавы таким способом не настроить. Для получения других ступеней нужно применять последовательное использование кварт или квинт.

Рассмотрим сначала последовательную настройку по чистым квартам от ноты А₂ вверх и от ноты а² вниз. Тогда на ноте es (dis) процесс настройки закончится. Этот процесс настройки происходит за 6 шагов. Интервал А₂ – а² равен 5 октавам. Интервальный коэффициент чистой кварты равен 4/3. Тогда при настройке снизу вверх нота es будет иметь частоту колебаний:

,

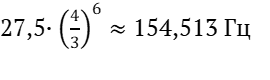где 27,5 Гц – частота колебаний ноты А₂.

При настройке сверху вниз частота ноты dis будет следующей:

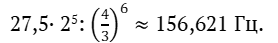
Как видно, частота одной и той же ноты оказалась разной. Это означает, что такой способ настройки, предложенный Пифагором, оказался несостоятельным.

Найдём отношение частот этой ноты: большей к меньшей.

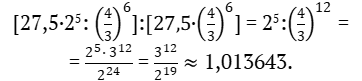
Теперь рассмотрим последовательную настройку по чистым квинтам от ноты А₂ вверх и от ноты а⁴ вниз. Процесс настройки закончится на ноте dis¹ (es¹). Интервал А₂ – а⁴ равен 7 октавам. Процесс настройки происходит также за 6 шагов. Интервальный коэффициент чистой квинты равен 3/2.

При ходе снизу вверх частота ноты dis¹ будет равна

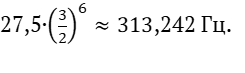
При ходе сверху вниз частота ноты es¹ будет равна

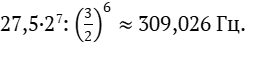
Отношение полученных частот: большей к меньшей равно

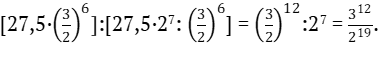
Эти два отношения получились одинаковыми и называются пифагоровой коммой [1].

Указанные две последовательности настройки отражены на рисунке 3.

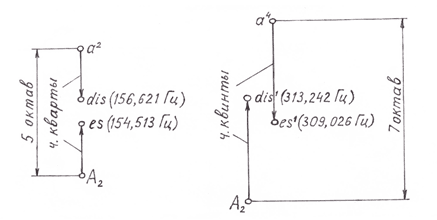
Рис. 3. Схема двух последовательностей настройки

Найдём, какую часть октавы составляет пифагорова комма. Для этого воспользуемся формулой

2^x = p,  (9)

где p является пифагоровой коммой; .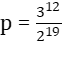

Для определения х нужно прологарифмировать обе части этой формулы (9).

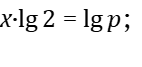
отсюда 

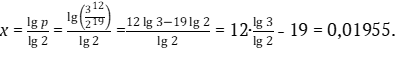
Применительно к полутону пифагорова комма будет в 12 раз больше, т. е. 12·0,01955 =0,2346.

Таким образом, пифагорова комма составляет 0,2346 полутона, что заметно для слуха.

Для избегания пифагоровой коммы в XVI веке в Европе стали применять равномерно темперированный строй (РТС), при котором интервал чистая октава делится на 12 равных частей – полутонов.

4. Составление таблицы гармонического ряда и номеров полутона для двух планов настройки

Для определения частоты колебаний основного тона (первой гармоники) нужно в формуле (4) считать переменной только длину l. Тогда эта формула с учётом формулы (3) примет вид:

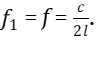  (10)

Для i-й гармоники частота колебаний 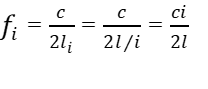  или выражая f_i через  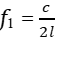, получим

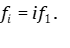   (11)

Для перевода частоты f_i i-й гармоники в частоту какого-либо полутона нужно воспользоваться уравнением частоты для полутона

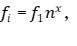     (12)

где n – интервальный коэффициент полутона,

x – номер полутона, считая x = 0 для звука с частотой f₁.

Приравнивая правые части формул (11) и (12), найдём x.

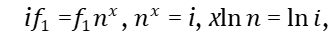
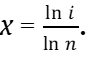 (13)

Существуют разные планы настройки. Рассмотрим планы настройки по чистым октавам и чистым дуодецимам.

При плане настройки по чистым октавам, который является наиболее распространённым, с увеличением высоты звука на одну октаву его частота возрастает ровно в два раза. Так как в октаве 12 полутонов, то при повышении звука на полутон его частота возрастает в 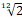, то есть в ту величину 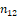, которая и является интервальным коэффициентом полутона.

При настройке по чистым дуодецимам, которая была предложена Б. Штоппером, с увеличением высоты звука на одну дуодециму его частота возрастает ровно в три раза. В дуодециме 19 полутонов, поэтому интервальный коэффициент полутона 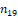 составляет .

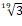Обобщим обозначение интервального коэффициента полутона применительно к указанным планам настройки:

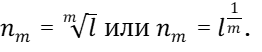      (14)

Здесь для плана настройки по чистым октавам l = 2, m = 12, а для плана настройки по чистым дуодецимам l = 3, m = 19.

Значения интервальных коэффициентов полутона для указанных планов настройки с точностью до девятого знака после запятой составляют:

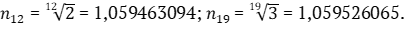
Составим таблицу 1 гармонического ряда для первых 17 гармоник (i) с их частотами f_i. В эту таблицу для двух планов настройки также входят номера x полутонов и ближайшие к ним ноты с отклонениями (±) в центах. За первую гармонику с нулевым номером полутона примем ноту А₂ (ля субконтроктавы).

Таблица 1

Как видно из приведённой таблицы 1, номера x полутонов в большинстве случаев отличаются от целых чисел на ту или иную величину. Чем больше это отличие, тем больше частота этого полутона отличается от частоты соответствующей гармоники.

5. Вывод формулы числа биений

Из курса «Физики» известно, что при одновременном возбуждении колебаний двух струн с близкими частотами возникают так называемые биения – периодические усиления громкости их звучания. Формула биений Δ имеет вид:

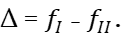 (15)

Число биений Δ = 0, если как видно из формулы (15),  f_Ι˗ f_ΙΙ = 0 или  f_Ι= f_ΙΙ.

Взяв два каких-либо звука 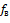 и 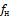из гармонического ряда, запишем, используя формулу (11):

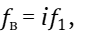(16)

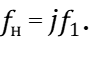   (17)

Тогда, чтобы получить равные частоты  f_Ι и f_ΙΙ, нужно умножить f_в на j, а f_н  на i.

Получим

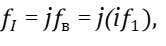 (18)

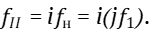   (19)

Действительно, имеем

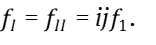
Подставив (18) и (19) в уравнение (15), получим:

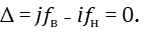          (20)

Если частоты f_в и f_н взяты из гармонического ряда, то частота биений Δ, как следует из формулы (20), равна нулю. Если же  f_в и f_н являются частотами равномерно темперированного строя с каким-либо планом настройки, то в общем случае число биений вычисляется так же, как в формуле (20), но без нуля в правой части. То есть, имеем:

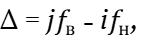 (21)

где f_н и f_в ˗ частоты колебаний нижней и верхней ступеней интервала,

i, j – номера гармоник нижней и верхней ступеней интервала соответственно на уровне частот, где считают биения. Эти номера берутся такими, чтобы число биений было наименьшим. (Чем меньше число биений, тем проще настройщику их считать).

Формула (21) соответствует формуле, взятой из [4].

6. О нахождении номеров гармоник для разных интервалов

Рассмотрим пример нахождения гармоник i, j для какого-нибудь интервала. Возьмём интервал малую терцию. Обратившись к таблице 1, видим, что этот интервал находится между двумя парами звуков: cis – e и e – g. Наибольшее отклонение гармонической частоты у этих трёх нот: cis, e и g имеется у ноты g (составляет 31,174 цента). Остаётся пара звуков: cis – e. У этих нот гармониками являются цифры 5 и 6. Тогда i = 6, а j = 5. Если взять этот же интервал, но расположенный на октаву выше, то i и j увеличатся в два раза (i = 12, j = 10). Соответственно этому в два раза возрастает и число биений, что не удобно настройщику для прослушивания тем более, что эти биения надо слушать на октаву выше. Кроме того, как видно из формулы (8) громкость гармоники, расположенной на октаву выше, уменьшается в 2 раза, что труднее для прослушивания.

Итак, делаем вывод: значения i, j должны быть целыми числами, не делящимися одновременно на 2.

Обратимся к формуле (21). Эта формула не удобна для анализа тем, что число биений Δ зависит не от одной переменной, а от двух (f_н и f_в). Уменьшим число переменных в этой формуле до одного.

Частоту колебаний верхней ступени интервала можно связать с частотой колебаний нижней ступени на основании следующих рассуждений. Известно, что при равномерной темперации отношение частот колебаний любых соседних полутонов является постоянной величиной. Этой постоянной величиной, как было ранее указано, является интервальный коэффициент полутона .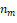

Для любого интервала интервальный коэффициент равен 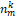, где k – номер верхней ступени интервала, считая для нижней ступени k = 0.

С учётом (14) интервальный коэффициент будет иметь вид:

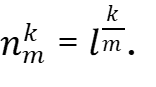   (22)

Тогда можно записать, что частота колебаний верхней ступени

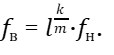    (23)

Подставив формулу (23) в (21), получим число биений интервала 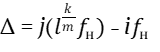 или

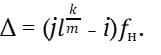  (24)

Итак, получили формулу, в которой число биений зависит только от одной переменной – f_н.

Можно было бы, используя формулу (23), выразить f_н через f_в и подставить f_н в формулу (21). Тогда число биений будет выражено через f_в. Но особой необходимости в этом нет, поэтому ограничимся формулой (24) для Δ.

7. Вывод формулы для коэффициента биений интервала

Посмотрим на формулу (24) с другой стороны. Как видно из этой формулы, число биений Δ является произведением двух сомножителей. Первый сомножитель, стоящий в скобках, является для определённого интервала постоянным числом, так как величины i, j, k, l, m, входящие в него – постоянные числа. Второй сомножитель f_н является переменным числом или, выражаясь по-другому, размерным масштабом абсолютной величины Δ.

Разделив абсолютную величину Δ на масштаб , получим относительную величину

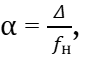     (25)

где

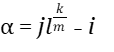   (26)

назовём коэффициентом биений интервала. Этот коэффициент, как указано выше, является постоянной величиной и, можно сказать, характеризует «окраску» интервала.

8. Таблица коэффициентов биений интервалов для двух планов настройки

Приведём таблицы коэффициентов биений интервалов для двух планов настройки: по чистым октавам (l = 2, m = 12) (таблица 2) и чистым дуодецимам (l = 3, m = 19) (таблица 3). Коэффициенты биений интервалов соответственно имеют вид:

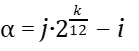  (27)

и

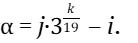   (28)

Таблица 2

Таблица 3

В таблицах 2 и 3 приведены значения коэффициентов биений α для всех интервалов, входящих в зону темперации. В этих таблицах указаны также величины гармоник i, j и номер k верхней ступени интервала. Название интервалов взято в соответствии с источником [5].

Используя величину коэффициента биений интервала α, входящего в тот или иной план настройки, можно определить число биений Δ, используя приведённую частоту колебаний  нижней ступени интервала. Это число биений определяется из формулы (25) и имеет вид:

Δ = α· f_н.   (29)

Знак «плюс» в коэффициенте α означает, что интервал должен настраиваться шире чистого интервала, т. е. с расширением, а «минус» - что интервал должен быть настроен у́же чистого интервала, т. е. с сужением.

Повторим, что наиболее часто используется план настройки по чистым октавам.

Использование коэффициента биений α и формулы (29) заменяет обширные таблицы с частотами биений интервалов, приведёнными, например, в источниках [4] и [6].

Приведём пример определения коэффициента биений интервала для большой терции, у которой i = 5, j = 4, k = 4. План настройки возьмём по чистым октавам. Используя формулу (27), получим

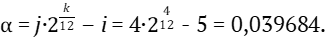
Определим теперь число биений для этого интервала, нижней ступенью которого является ля малой октавы. Частота колебаний этой ноты, как видно из таблицы 2, f_н = 220 Гц. Тогда, используя формулу (29), получим:

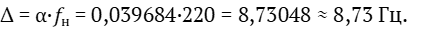
Это число биений настройщику нужно слушать, как видно из таблицы 2, на уровне i-й гармоники нижней ступени интервала, т. е. ноты ля малой октавы. Пятая (i = 5) гармоника этой ноты отстоит вверх от неё на 2 октавы и б. терцию. Такой нотой является до-диез третьей октавы. Если такое число биений соблюдается, то данная нота cis¹ настроена точно по равномерно темперированному строю (РТС).

Возьмём другой пример без использования формулы (27). Чтобы настроить чистую квинту с использованием плана настройки по чистым октавам от ноты ля малой октавы вверх, т. е. ноту ми первой октавы, из таблицы 2 берём α = - 0,003385846 и умножаем на f_н   = 220. Получаем с использованием формулы (29): Δ = α· f_н = ˗0,003385846·220 = ˗0,74488612 ≈ ˗0,745 Гц. Найденное число биений с учётом сужения интервала нужно слушать на уровне одной октавы с чистой квинтой выше ноты ля малой октавы. Таким уровнем является нота ми второй октавы. Для облегчения счёта нужно умножить это число биений, например, на пять. Получим -0,745·5 ≈ ˗ 3,7 биения. Это означает что, отсчитывая по секундной стрелке часов или по секундомеру 5 секунд, число биений должно быть чуть меньше 4 биений с учётом сужения интервала.

Рассмотрим ещё один пример: найти число биений и уровень этих биений для интервала c¹ - f¹​​​​ (чистая кварта) при использовании обоих планов настройки. Число биений будем определять по формуле (29). Нижней ступенью в данном интервале является нота c¹, поэтому частоту f_н нужно брать для этой ноты. Выбирая величины α и f_н из таблицы 2, определяем число биений Δ для плана настройки по чистым октавам:

Δ = α∙ f_н  = 0,004519562∙261,625565 ≈ 1,182 Гц.

Выбирая величины α и f_н из таблицы 3, определяем число биений Δ для плана настройки по чистым дуодецимам:

Δ = α∙ f_н  = 0,005709769∙261,485657 ≈ 1,493 Гц.

Уровень биений для чистой кварты расположен на две октавы выше нижней ступени, которой является нота c¹. Значит, слушать вычисленные биения нужно на уровне ноты до третьей октавы.

9. Проверка настройки зоны темперации

После настройки зоны темперации, которая составляет одну октаву (а-а¹) при использовании плана настройки по чистым октавам и одну дуодециму (a-e²) при использовании плана настройки по чистым дуодецимам, полезно сделать проверку парных интервалов с равными биениями. Эти парные интервалы имеют два вида, получаемые переносом нижней или верхней ступени первого интервала на октаву или дуодециму вверх в соответствии с планом настройки.

Проведём теоретическое обоснование этих парных интервалов с равными биениями, используя формулу (24).

В парных интервалах первого вида число биений одинаковое, но эти биения имеют разные знаки. В парных интервалах второго вида число биений одинаковое и знаки этих биений одинаковы.

Рассмотрим примеры парных интервалов.

Начнём с парных интервалов первого вида, образуемых переносом нижней ступени.

План настройки по чистым октавам - интервалы: (a-d¹, d¹-a¹), их числа биений: (0,994;-0,994), гармоники i, j этих интервалов: (i₁ = 4, j₁ = 3; i₂ = 3, j₂ = 2).

План настройки по чистым дуодецимам - интервалы: (а-с¹, с¹-е²), биения: (-11,631;11,631), гармоники i, j: (6-5, 5-2).

Обозначая индексы гармоник буквами i, j и номер k верхней ступени первого интервала цифрой 1, а второго интервала цифрой 2, запишем:

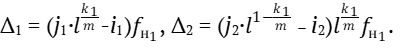
Из примера видно, что 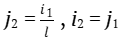. Учитывая разные знаки биений, запишем: Δ₁ + Δ₂ =0 или

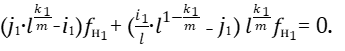
Проверим это тождество.

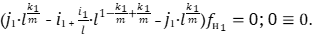
Тождество выполняется.

Перейдём к парным интервалам второго вида, образуемых переносом верхней ступени.

План настройки по чистым октавам – интервалы: (a – cis¹, a – cis²), биения: (8,731; 8,731), гармоники i, j: (5 – 4, 5 – 2).

План настройки по чистым дуодецимам - интервалы: (a – d¹, a – a²), биения: (1,255; 1,255), гармоники i, j: (4 – 3, 4 – 1).

Биения первого и второго интервалов:

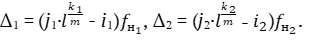
Взаимосвязь величин с индексами 2 и 1 в соответствии с примером:

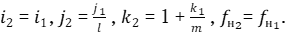
Тогда 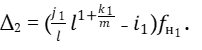Учитывая, что Δ₁ =Δ₂, запишем:

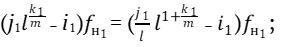
Проверим тождество.

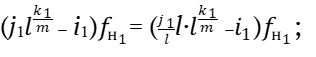
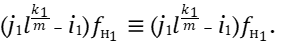
Тождество выполняется.

На этом доказательство равенства биений некоторых парных интервалов двух видов заканчивается.

Если каждую ступень нижнего интервала из какого-нибудь парного интервала с равными биениями поднять на октаву (при плане настройки по чистым октавам) или на чистую дуодециму (при плане настройки по чистым дуодецимам), то число биений поднятого интервала увеличится соответственно в 2 и 3 раза. Такие парные интервалы назовём парными интервалами с двойными (тройными) биениями. Так как каждый парный интервал с двойными (тройными) биениями образуется из парного интервала с равными биениями, то число парных интервалов с двойными (тройными) биениями равно числу парных интервалов с равными биениями.

Итак, получены признаки равенства биений парных интервалов: если целым числом является дробь 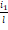, то это парный интервал первого вида, а если целым числом является дробь  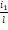, то это парный интервал второго вида. Здесь индекс 1 в числителях указанных дробей означает, что рассматривается первый интервал из каждого парного интервала.

На основании этих признаков выберем по гармоникам i, j, приведённым в таблицах 2 и 3, все первые интервалы, способные образовать парные интервалы двух видов.

План настройки – чистая октава.

Парные интервалы с равными биениями:

а) первый вид

б) второй вид

Парные интервалы с двойными биениями:

а) первый вид

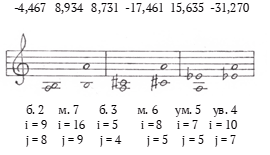
б) второй вид

План настройки – чистая дуодецима.

Парные интервалы с равными биениями:

а) первый вид

б) второй вид

Парные интервалы с тройными биениями:

а) первый вид

б) второй вид

10. О графике частот для полутонов и центов

Используем формулу (11) для частот полутонов всего звукоряда фортепиано применительно к плану настройки по чистым октавам. Уравнение частот f(x) для полутонов имеет вид:

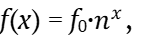 (30)

где f₀ =27,5 Гц – частота ноты А₂,

x ϵ [0; 88] – номер полутона, считая x = 0 для ноты А₂,

n = n₁₂ = 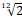  – интервальный коэффициент полутона.

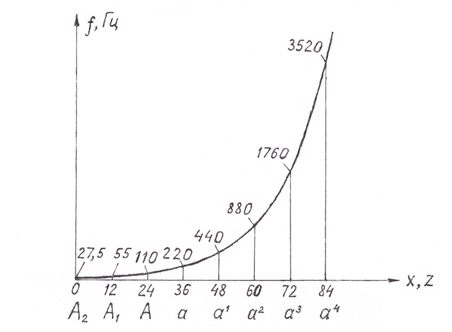
Рис. 4. График частот нот

На рисунке 4 показан график показательной функции, соответствующей уравнению (30).

Настройщикам фортепиано приходится иметь дело с более маленькими интервалами, чем полутон. Цент делит полутон на 100 равных частей. Интервальный коэффициент цента поэтому равен 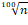. Обозначив номер цента буквой z ϵ [0; 8800], считая z = 0 для ноты А₂, получим уравнение частот для центов

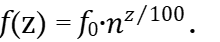  (31)

График этого уравнения полностью совпадает с графиком уравнения частот для полутонов.

Для показательной функции шаг по оси абсцисс (x, z) равномерный, он возрастает с ростом номеров x и z. Определим шаги ступеней в Гц, соответствующие полутону и центу. Эти шаги будут найдены после взятия первой производной от уравнений (30) и (31).

Найдём шаг ступени, соответствующий одному полутону.

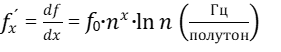
или

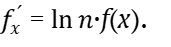 (32)

Так как 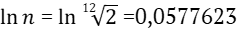 , то

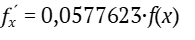    (33)

Найдём шаг ступени, соответствующий одному центу.

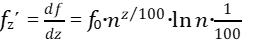
или

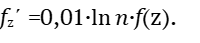  (34)

С учётом значения ln n

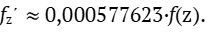   (35)

Как видно из формул (32) и (34), для определённого значения z = 100x шаг ступени в Гц, соответствующий одному центу, в 100 раз меньше шага ступени, соответствующему одному полутону.

Например, для ступени x = 48, соответствующей ноте а¹ с частотой 440 Гц, шаг ступени размером в полутон f_x^ˊ  = 0,0577623·440 = 25,4154, а для той же ступени z = 100x =100·48 =4800 шаг ступени размером в цент f_zˊ = 0,000577623·440 = 0,254154 Гц/цент.

Изобразим на рисунке 5 шаги dz и df, соответствующие рассмотренной ноте a¹.

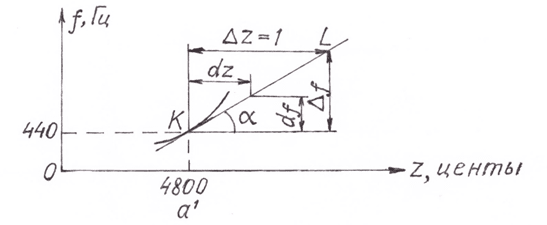
Рис. 5. Шаги dz и df

На этом же рисунке показан отрезок KL касательной, проведённой к графику в точке K. Угловой коэффициент этой касательной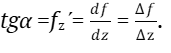 

Рассмотрим два звука: один из них имеет номер цента, соответствующий ноте a¹ (z₁ = 4800), а номер цента другого звука отличается от номера цента первого звука на малую величину, например, z₂ =4801. Имеем Δz = z₂ – z₁ = 4801 – 4800 = 1цент. В таком случае при одновременном звучании двух звуков возникают биения с частотой Δf = f₂ – f₁. Для ноты a¹ эти биения, как вычислено, составляют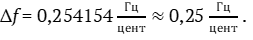

В данном случае эти биения возникают между частотами основных звуков, а не между их гармониками. Герц это – одно колебание в секунду или в данном случае одно биение в секунду. Тогда можно записать следующее:

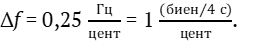
11. Способ проверки музыкального слуха настройщика

Исходя из этих рассуждений, можно предложить следующий способ проверки музыкального слуха настройщика.

1. Заглушив одну из трёх струн хора a¹, настроим по возможности в унисон (как позволит музыкальный слух) две других струны.
2. Чуть-чуть изменим высоту одной из этих двух струн, пока не ощутим на слух разницу в их высоте.
3. Пользуясь секундомером, в течение четырёх секунд считаем число биений расстроенного унисона.

Это число биений и будет мерилом музыкального слуха в центах.

Как сказано в инструкциях, опытный настройщик обязан различать интервал в 1⁄100 тона, что составляет два цента.

Известно, что с годами музыкальный слух настройщика утончается или, иначе говоря, уменьшается его дифференциальный порог.