О спектре оператора Лапласа-Бельтрами на двухмерной сфере

В настоящей работе производится изучение оператора Лапласа-Бельтрами L₀, определяемого по формуле:

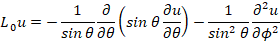, (1) 

и его возмущения 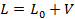 в 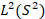, где V – оператор умножения на функцию .

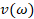Прежде асимптотика спектра и формула следов данных операторов изучались в различных трудах, причем формула следов была получена при условии 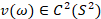 (см., например, [1]). Дальнейшее ослабление требований на возмущение  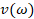связано с более подробным знанием свойств ядра  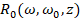невозмущенной резольвенты 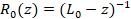, которые мы и намерены изучить.

Известно, что ядро 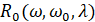   равно

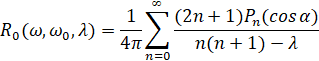, (2)

где α - угол между векторами 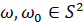, P_n(x) - полином Лежандра, нормированный условием P_n(1)=1, а  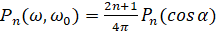есть ядро ортогонального проектора Ρ_n, проектирующего на собственное подпространство, соответствующее собственному числу λ_n=n(n+1). Кратность λ_n равна 2n+1.

С другой стороны, известно (см., например, [2], с.66-71), что последовательность

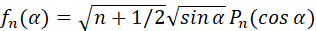, n=0,1,..  (3)

образует ортонормированный базис собственных функций обыкновенного дифференциального оператора M в 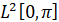, порожденного дифференциальным выражением

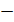
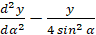 (4)

и нулевыми граничными условиями в точках α=0 и α=π , причем fn(α)    есть собственная функция оператора M, соответствующая собственному числу .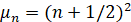

Так что, согласно (3), ядро G(α,α0,z)  интегрального оператора  G(z)=(M-z)-1 представляется в виде

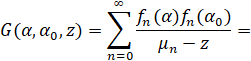
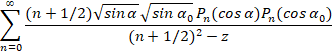   (5)

Положим

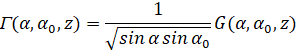  (6)

Тогда из (5) следует, что

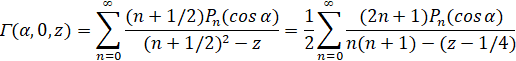(7)

Сравнивая (2) и (7) между собой, мы видим, что если подставить в  Г(α,α₀,z) значения α₀=0 и 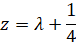, то получившаяся величина будет совпадать с R₀(ω,ω₀,λ) с точностью до множителя 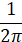. Учитывая всё вышесказанное, мы приходим к следующему утверждению.

Лемма 1.

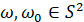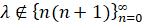Для всех  и   ядро 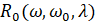 представляется в виде

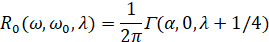 (8)

Таким образом, из равенств (6)-(8) видно, что ядро 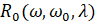 может быть представлено посредством решений обыкновенного дифференциального уравнения

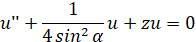   (9)

на интервале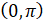 

Вначале заметим, что на промежутке (0,π/2]  справедливо равенство 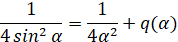, (10)

где 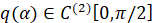 . Из (3)-(10) вытекает, что линейно независимые решения уравнения (9) можно построить с помощью решений уравнения

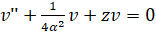  (11)

В качестве линейно независимых решений «невозмущенного» уравнения (11) возьмем функции(см. [2])

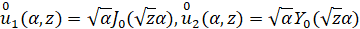, (12)

где 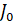  и 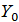  и - соответственно, функции Бесселя первого и второго рода, 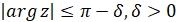- сколь угодно малое фиксированное число. Хорошо известно, что вронскиан

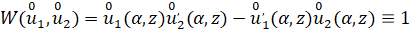 (13)

Теперь в качестве линейно независимых решений уравнения (9) на промежутке 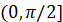 рассмотрим решения неоднородных вольтерровых уравнений

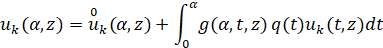, (14)

где 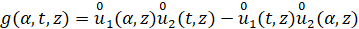   (15)

В итоге мы свели процесс изучения свойств ядра к свойств функций, выражающихся через функции Бесселя, чьи свойства достаточно хорошо изучены. Полученный переход позволяет нам значительно упростить решение изначально поставленной задачи, о чем будет подробнее рассказано в последующих работах.