Условия равномерной экспоненциальной устойчивости дифференциальных уравнений

Рассмотрим дифференциальное уравнение с малым параметром вида

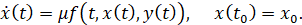     (1)

В этом уравнении функция f:R₊×Rⁿ×R^m→Rⁿ, y:R₊→R^m, y(⋅)∈Y, где Y – подмножество множества всех измеримых функций, μ – малый параметр, 0≤μ≤μ_*,   μ_*>0.

Определим решение системы (1) с начальным условием x(t₀)=x₀∈Rⁿ как абсолютно непрерывную функцию x(t), удовлетворяющую системе (1) почти при всех t≥t₀ и для всех функций y(⋅)∈Y.

Положение равновесия 0∈Rⁿ системы (1) будем называть равномерно экспоненциально устойчивым, если существуют такие постоянные A>0, α>0, и μ₀>0, что для всех значений малого параметра возмущения μ ∈ (0, μ₀] любых начальных условий (t₀,x₀)∈R₊×Rⁿ, времени t≥t₀ и всех функций y(⋅)∈Y, соответствующие траектории (1) удовлетворяют оценке

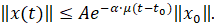
Одновременно с задачей Коши для уравнения (1) рассмотрим усредненную задачу Коши, которая описывается неавтономным дифференциальным включением

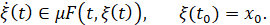              (2)

В правой части отображение F:R₊×Rⁿ→Kv(Rⁿ), где Kv(Rⁿ) – класс непустых компактных выпуклых множеств из Rⁿ.

Нулевое решение задачи (2) будем называть равномерно экспоненциально устойчивым, если существуют постоянные A>0, β>0, и μ₁>0, такие что для всех значений параметра μ∈ (0,μ₁] для любых начальных условий (t₀,x₀) ∈ R₊×Rⁿ и любого решения ξ(t) задачи (2) справедливо неравенство

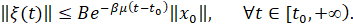
Условия, при которых равномерная экспоненциальная устойчивость усредненной системы наследуется возмущенной системой (1) при малых значениях параметра возмущения μ>0, рассматривались в работах [4, 1]. В частности, в статье [4] доказано, что при условии липшицевости правых частей возмущенной и усредненной систем, а также при некоторых дополнительных предположениях, из равномерной экспоненциальной устойчивости автономной усредненной задачи следует равномерная экспоненциальная устойчивость исходной задачи [4, теорема 3.1]. Авторы этой статьи считают условие Липшица существенным для доказанной теоремы.

Однако, в [1] доказано достаточное условие равномерной экспоненциальной устойчивости для более общего случая неавтономной системы сравнения, причем условие липшицевости правой части дифференциального включения (2) заменено на более слабое условие односторонней липшицевости [3], а от функции f в правой части исходной задачи (1) не требуется даже этого условия, но предполагается существование решения. Отсутствие липшицевости правых частей f и F из задач (1) и (2) компенсируется предположением линейного роста и условиями, обеспечивающими для отображения 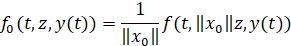 равномерную непрерывность по переменной z а для отображения  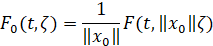– равномерную полунепрерывность сверху по фазовой переменной, равномерную по t на R₊. Для доказательства этой теоремы существенно используется критерий равномерной экспоненциальной устойчивости, доказанный в [2, теорема 1] для дифференциальных включений. Приведем этот критерий, сформулировав его для рассматриваемых нами задач (1) и (2).

Предположим, то существует неубывающая функция Γ:0,+∞)→R₊ такая, что для произвольных начальных данных (t0,x0)∈R₊×Rⁿ и любого решения задачи (1) справедлива оценка

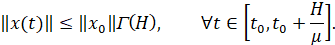   (3)

Постоянная H>0 выбирается так, чтобы выполнялось неравенство

p<1,       p=Be^-βH,  (4)

где B и β – постоянные из определения равномерной экспоненциальной устойчивости усредненной системы.

Основное условие критерия равномерной экспоненциальной устойчивости формулируется следующим образом:

(*) для некоторых постоянных H и p, удовлетворяющих неравенству (4), существуют постоянные q∈[0,1), μ2>0 такие, что p+q<1 и для любых начальных условий (t₀,x₀) ∈ R₊×Rⁿ и любого решения x(t) задачи (1) найдется такое решение усредненной задачи (2), для которого

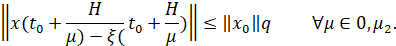
Теорема 1 [2, критерий равномерной экспоненциальной устойчивости]. Пусть для любого решения задачи (1) имеет место неравенство (3), и усредненная система (2) является равномерно экспоненциально устойчивой. Тогда для равномерной экспоненциальной устойчивости дифференциального уравнения (1) необходимо и достаточно, чтобы выполнялось условие (*).

Рассмотрим теперь пример из [4], демонстрирующий, по мнению авторов статьи, существенность условия Липшица для правой части возмущенной системы, и покажем, что отсутствие равномерной экспоненциальной устойчивости исходного дифференциального уравнения связано не с отсутствием липшицевости, а с невыполнением априорных оценок в теореме 1.

Пример [4, пример 4.3]. Рассмотрим возмущенное дифференциальное уравнение

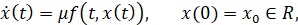 (5)

где для x>0 определим

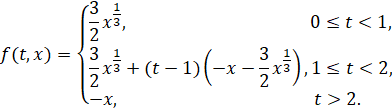
При x≤0 и t≥0 определим f(t,x)=-f(t,-x), и f(t,0)=0 при всех t≥0.

Отображение f(t,x) непрерывно на [0,+∞)×R, но не липшицево по переменной x. Однако, кроме этого, для системы (5) не выполняется также априорная оценка решения (3), так как для любого фиксированного параметра возмущения μ>0 начальному значению x₀=0 соответствует траектория 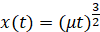 при t ∈ [0,1]. Очевидно, что начало 0∈R не является точкой равновесия экспоненциальной устойчивости для возмущенной системы.

В качестве системы сравнения рассмотрим дифференциальное уравнение

ξ=-ξ,  ξ(0)=x₀.

Усредненная система равномерно экспоненциально устойчива.

Таким образом, для достаточного условия равномерной экспоненциальной устойчивости дифференциальных уравнений с управлением существенным является выполнение априорной оценки (3). А эта оценка справедлива не только при условии липшицевости отображения f из задачи (1), но и при выполнении других условий, например, условия линейного роста, что и было использовано в работе [1].