Введение. Вопросам оптимального управления для моделей экономики посвящены работы многих исследователей [1,3-5]. В основном рассматривается непрерывное управление. Представляет интерес сравнение алгоритмов непрерывного и дискретного методов управлений.
Уравнение Солоу записывается в виде
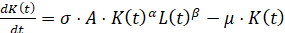 ,
,  . (1)
. (1)
В этом уравнении  – объем основных фондов в момент времени t,
– объем основных фондов в момент времени t,  – затраты на трудовые ресурсы. Параметрами уравнения являются: μ>0 – темп выбытия основных фондов, А – коэффициент, учитывающий уровень технического прогресса, 0≤σ≤1 – доля инвестиций на обновление основных фондов, α,β – параметры производственной функции, которая принята в виде функции Кобба-Дугласа:
– затраты на трудовые ресурсы. Параметрами уравнения являются: μ>0 – темп выбытия основных фондов, А – коэффициент, учитывающий уровень технического прогресса, 0≤σ≤1 – доля инвестиций на обновление основных фондов, α,β – параметры производственной функции, которая принята в виде функции Кобба-Дугласа:
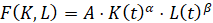 .
.
На рис. 1(а) изображена схема финансовых потоков. Баланс финансовых потоков определяется равенством
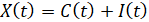 ,
,
где 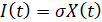 ,
, 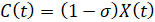 .
.
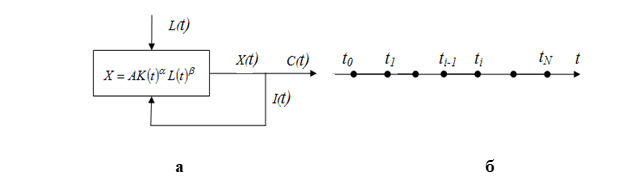
Рис. 1. (а) Схема финансовых потоков; (б) Дискретное время
В [4] рассмотрена следующая задача: найти такое управление 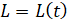 , при котором за время
, при котором за время 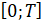 капитал
капитал 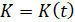 вырастет от
вырастет от 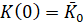 до
до 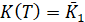 . При этом интегральный функционал
. При этом интегральный функционал
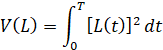 (2)
(2)
примет минимальное значение.
Математическая формулировка непрерывной задачи имеет вид:
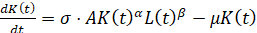 ,
, 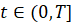 (3)
(3)
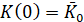 ,
, 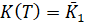 , (4)
, (4)
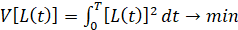 . (5)
. (5)
Система уравнений Эйлера для расширенного функционала задачи (3)-(5) приводилась к следующему виду:
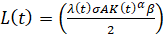 ,
, 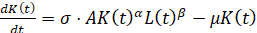 ,
,
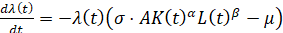 .
.
Для поиска решения представленной системы уравнений применялась явная схема численного метода Эйлера.
1. Дискретная задача. На практике изменение управляющей переменной L(t) возможно только в определенные моменты времени и принятая величина не меняется некоторый конечный период времени.
При переходе к дискретной задаче выполняются преобразования:
1. Непрерывная область изменения времени заменяется дискретной, то есть [0,T] отрезок заменяется дискретным множеством точек (рис. 1(б)):
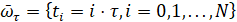 ,
, 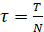 .
.
2. Производная заменяется разностным отношением и, таким образом, получаем дискретную задачу
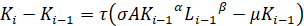 , (6)
, (6)
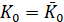 ,
, 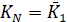 , (7)
, (7)
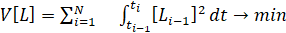 . (8)
. (8)
Необходимо найти такое управление 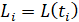 ,
, 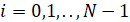 , при котором за время
, при котором за время 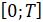 капитал
капитал 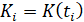 вырастет от значения
вырастет от значения 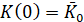 до значения
до значения 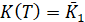 . При этом функционал (8) примет минимальное значение.
. При этом функционал (8) примет минимальное значение.
При условии 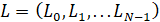 , где
, где 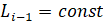 при
при 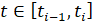 , интеграл (8) можно преобразовать, тогда вместо (8) получим условие
, интеграл (8) можно преобразовать, тогда вместо (8) получим условие
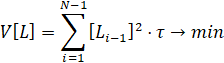 . (9)
. (9)
Заметим, что 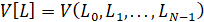 – функция N переменных. Переменные K1, K2,...,KN содержатся в уравнении связи (6). Таким образом, сформулирована задача на условный экстремум функции многих переменных. Для поиска решения воспользуемся методом множителей Лагранжа [2, 6].
– функция N переменных. Переменные K1, K2,...,KN содержатся в уравнении связи (6). Таким образом, сформулирована задача на условный экстремум функции многих переменных. Для поиска решения воспользуемся методом множителей Лагранжа [2, 6].
Составляем функцию Лагранжа:
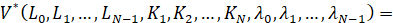
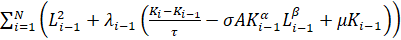 .
.
Запишем необходимые условия существования экстремума
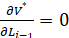 ,
, 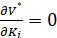 ,
, 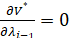 ,
, 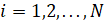 .
.
Приравнивая к нулю производные, получаем уравнения
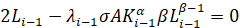 , (10)
, (10)
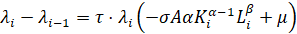 , (11)
, (11)
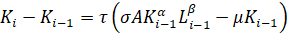 . (12)
. (12)
Кроме того, должны выполняться условия:
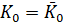 ,
, 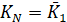 (13)
(13)
Рассмотрим алгоритм решения системы уравнений (10)-(12).
Из уравнения (10) выражаем Li-1≠0:
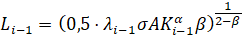 (14)
(14)
При заданном значении λ0 находим L0.
Из (11) следует (при i=1,2,...,N-1)
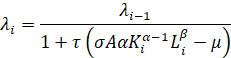 (15)
(15)
Из уравнения (12) находим
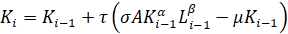
При известных значениях Ki, Li-1 и λi-1 строится итерационный процесс:
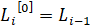 ,
, 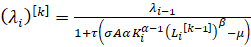 , (16)
, (16)
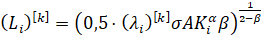 ,
, 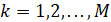 . (17)
. (17)
Решение задачи (10)-(13) зависит от выбора начального значения 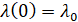 . Методом вариации данного начального значения находится такое значение
. Методом вариации данного начального значения находится такое значение 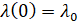 , при котором
, при котором 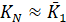 . Для реализации метода вариации начального значения λ0 составляем целевой функционал
. Для реализации метода вариации начального значения λ0 составляем целевой функционал
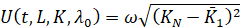 , (18)
, (18)
где ω – постоянная.
Минимум функционала (18) определяется итерационным процессом:
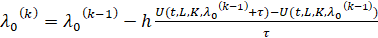 ,
, 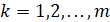 . (19)
. (19)
2. Алгоритм решения дискретной задачи. Функциональная схема программы в системе Mathcad приведена на рис.2.
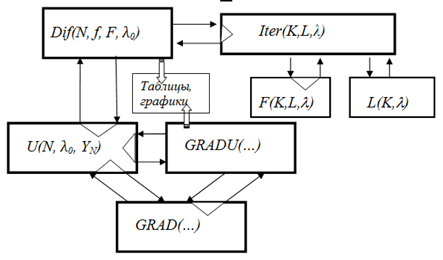
Рис. 2. Функциональная схема программы
В программе функция L(K, l) определяет оптимальное значение трудовых ресурсов (14); Dif(N, f, F, λ0) предназначена для решения системы уравнений (10)-(12); f(K, L ) – правая часть уравнения (12); F(K, L, l ) – правая часть уравнения (14); Iter(K, L, λ) – реализует итерационный процесс на каждом временном шаге для поиска решения системы (10)-(12); U(N, λ0 ,Yν) – вычисляет отклонение второго краевого условия от заданного значения. Управление методом градиентного спуска реализовано в блоках GRADU(… ) и GRAD(…). Результаты вычислений представлена на рис. 3, 4.
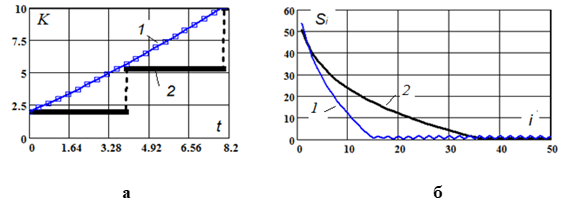
Рис. 3. (а) Оптимальный рост К: 1 – непрерывное управление; 2 – дискретное управление; (б) целевая функция в итерационном процессе
Оптимальное управление представлено на рис. 4. Следует отметить, что с увеличением числа шагов разность между непрерывным и дискретным управлением уменьшается.
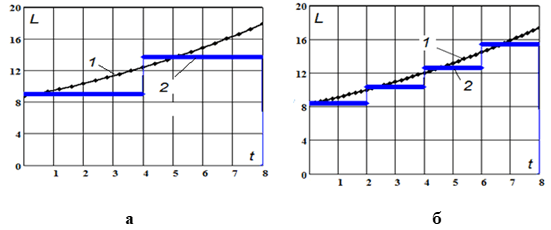
Рис. 4. Оптимальное управление: 1 – непрерывное, 2 – дискретное; (а) N=2 (б) N=4
Результаты сравнения значений затрат трудовых ресурсов при дискретном и непрерывном управлении приведены в таблице.
Таблица
Отношение оптимальных затрат в зависимости от количества промежутков
|
Число временных промежутков при дискретном управлении |
2 |
4 |
10 |
20 |
|---|---|---|---|---|
|
Отношение оптимальных затрат
|
0,834 |
0,926 |
0,979 |
0,947 |
Основные выводы
- Составлен алгоритм решения задачи дискретного оптимального управления для односекторной модели экономики. Построен итерационный процесс решения системы нелинейных алгебраических уравнений на каждом временном шаге.
- Разработана программа в системе Mathcad, реализующая алгоритмы дискретного и непрерывного управлений. Программа проверена в широком диапазоне параметров.
- Сравнительный анализ решений дискретного и непрерывного оптимальных управлений продемонстрировал существенное расхождение оптимальных решений при малом числе шагов для дискретного варианта. Оптимальные затраты трудовых ресурсов оказались меньше на 10…15% при дискретном управлении.

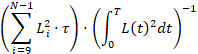
.png&w=640&q=75)