Постановка задачи
Производство пива представляет собой достаточно сложный технологический процесс и осуществляется в несколько этапов, каждый из которых требует тщательного контроля и качества. Одним из этапов является пастеризация.
Процесс пастеризации пива играет важную роль, увеличивая биологическую стойкость продукта и сохраняя его свойства. Пастеризация позволяет более полно освободить готовый продукт от дрожжей и других микроорганизмов.
Применяют пастеризацию в непрерывном потоке при температуре 67-75°С с выдержкой 15…30 секунд с дальнейшим охлаждением и нарушение этих параметров приводит к браку. Во избежание ухудшения качества пива, температурный режим пастеризации должен тщательно контролироваться и регулироваться [1].
Рассматриваемый объект управлений характеризуется неравномерностью распределения температур по своему объему, что позволяет рассматривать пастеризатор как объект с распределенными параметрами.
Основной задачей создания автоматической системы управления технологическим процессом пастеризация заключается в создании системы управления нагревательными элементами. Разработку системы управления будем производить с применением основ теории систем с распределенными параметрами [2].
Создание математической модели
Составим математическую модель для пастеризатора схема котла, которого представлена на рис. 1.
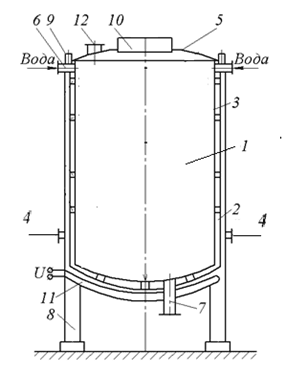
1. Цилиндрический сосуд. 2. Внешние стенки чана 3. Внутренние стенки сосуда. 4. Отвод пара. 5. Верхняя крышка. 6. Патрубок для технического обслуживания. 7. Патрубок для слива пива. 8. Опорные стойки. 9. Фиксирующие винты. 10. Электропривод. 11. Элемент нагрева. 12. Патрубок для выхода эстрапаров
Рис. 1. Схема пастеризатора
Математическую модель будем разрабатывать с применением уравнений математической физики [3]. Ниже представлен фрагмент математической модели.
Уравнение, описывающее тепловые процессы пива:
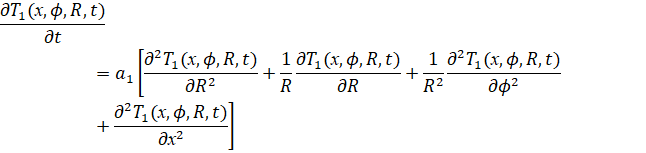 (1)
(1)
х0 ≤ x ≤ L1; R0 ≤ R ≤ R1; φ0 ≤ φ ≤ 3600
Уравнение 2 описывает тепловые процессы во внутреннем корпусе.
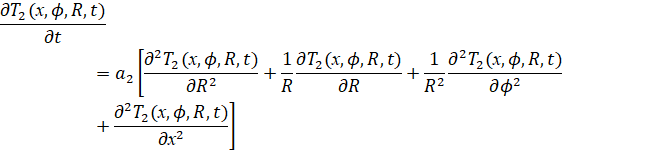 (2)
(2)
1) х0 ≤ x ≤ L2; R1 ≤ R ≤ R2; φ0 ≤ φ ≤ 3600
2) L1 ≤ x ≤ L2; R0 ≤ R ≤ R1; φ0 ≤ φ ≤ 3600
Уравнение 3 описывает тепловые процессы во внешней обшивке.
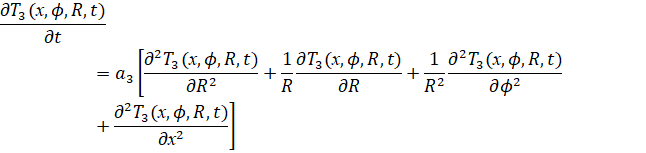 (3)
(3)
1) х0 ≤ x ≤ L3; R2 ≤ R ≤ R3; φ0 ≤ φ ≤ 3600
2) L2 ≤ x ≤ L3; R0 ≤ R ≤ R1; φ0 ≤ φ ≤ 3600
Считаем аппарат теплоизолированным с боковых сторон, таким образом, что тепловым воздействием извне можно пренебречь.
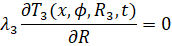 (4)
(4)
Запишем остальные граничные условия.
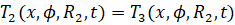 (5)
(5)
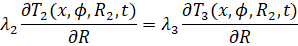 (6)
(6)
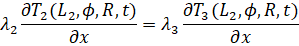 (7)
(7)
Для решения математической модели был выбран численный метод. С применением данного метода была составлена дискретная модель.
Решение полученной математической модели позволило построить графики переходного процесса в заданных точках.
Расчет настроек распределенного регулятора
Исследуемый объект не принадлежит к классу пространственно-инвариантных, т.е. решение не распадается по собственным вектор-функциям оператора объекта. Из этого следует, что определение границ расположения годографов собственных значений, может быть осуществлено с использованием спектров Гершгорина.
Исследуем распределенный объект управления, матрица передаточных коэффициентов которого имеет вид:
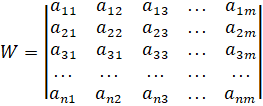 , где
, где 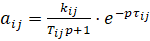 ,
,
Подавая на каждый вход объекта поочередно постоянный сигнал, на всех выходах получаем графики переходных процессов, из которых определяем kij, Tij, τij.
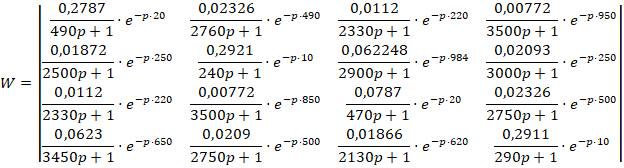
Затем определяем модуль и фазу для каждой составляющей матрицы строим спектры Гершгорина (рис. 2).
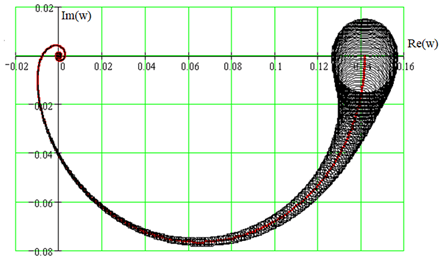
Рис. 2. Спектры Гершгорина по 3-ей секции объекта
Далее, с использованием полученных данных построим частотные характеристики объекта, с помощью которых производим расчет настроек распределенного регулятора.
Передаточная функция рассчитываемого распределенного регулятора, согласно [4], имеет вид:
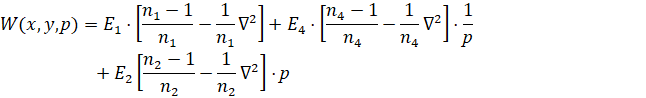
После расчета настроек запишем передаточную функцию полученного регулятора:
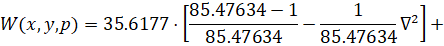
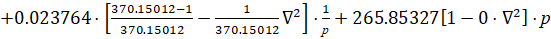 (8)
(8)
Далее был произведен анализ работы замкнутой системы управления.
Заключение
В данной работе были решены все поставленные задачи. Составлена математическая модель процесса пастеризации. Полученная модель позволила произвести анализ процессов, протекающих в объекте управления. На основе полученной информации были произведены расчета настроек распределенного регулятора. Моделирование производилось с применением C# в среде Visual studio и MATLAB Simulink. Результаты моделирования свидетельствуют о том, что полученная система может быть использована для управления технологическим процессом пастеризации.

.png&w=640&q=75)