Треугольник Рёло

Треугольник Рело по-другому еще называют «круглым» треугольником. Он представляет собой область пересечения трех равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Его строят последовательным проведением трех равных окружностей. Нужно провести две окружности с одинаковым радиусом, но так, чтобы центр второй совпадал с одной из точек первой (кроме центра). Проводим третью окружность, так что бы её центр совпадал с точкой пересечения первых окружностей. Область, которая принадлежит всем трем кругам и есть треугольник Рёло. Строят его с помощью одного только циркуля. Покажем на рис. 1.

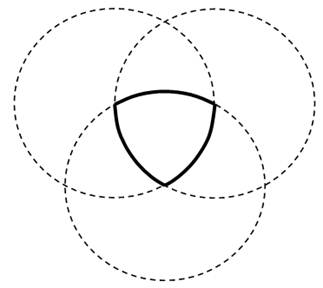
Рис. 1

Треугольник Рёло является плоской выпуклой геометрической фигурой. Через каждую вершину треугольника Рёло, в отличие от остальных его граничных точек, проходит не одна опорная прямая, а бесконечное множество опорных прямых. Пересекаясь в вершине, они образуют «пучок». Угол между крайними прямыми этого «пучка» называется углом при вершине. Для фигур постоянной ширины угол при вершинах не может быть меньше 120°. Единственная фигура постоянной ширины, имеющая углы, равные в точности 120° – это треугольник Рёло.

Если провести две параллельные прямые на некотором расстоянии, то фигура при качении будет касаться обеих прямых постоянно. Расстояние между ними и будет фигура постоянной ширины. Простейшей такой фигурой будет круг.

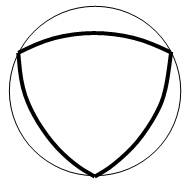
Рис. 2

Пусть а – это ширина фигуры, тогда площадь

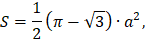
а периметр

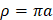 (рис. 2).

Также, треугольник Рёло используется в автомобильных двигателях, в грейферном механизме в кинопроекторах, в кулачковых механизмах швейных машин, механизме наручных часов. В форме треугольника Рёло можно изготавливать крышки для люков. Форма треугольника Рёло используется и в архитектурных целях. Например, построенная в 2006 году в Кёльне 103-метровая башня под названием «Кёльнский треугольник» в сечении представляет собой именно эту фигуру. Свойство треугольника Рело – качение по квадрату, позволяет применять его в интересных областях (рис. 3).

Рис. 3

Треугольник Рёло вписан в квадрат и может вращаться в нём, постоянно касаясь всех четырёх сторон. Каждая вершина треугольника при его вращении «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах – там вершина описывает дугу эллипса. Центр этого эллипса расположен в противоположном углу квадрата, а его большая и малая оси повёрнуты на угол в 45° относительно сторон квадрата и равны 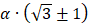(рис.3).

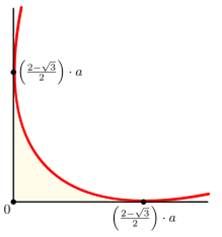
Рис. 4

Все 4 эллипса касаются смежных сторон квадрата на расстоянии 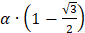 от угла (рис.4).

Среди всех многоугольников Рёло с фиксированным числом сторон и одинаковой шириной правильные многоугольники ограничивают. Если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным. Это расстояние называется шириной. Поскольку одна из прямых всегда проходит через вершину треугольника, а другая касается противоположной дуги, то ширина треугольника равна радиусу образующих его кругов (рис. 5) наибольшую площадь.

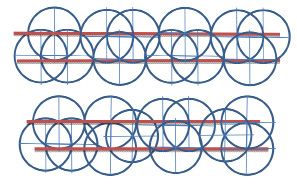
Рис. 5

Открытие треугольника Рёло сделало переворот в научно-техническом мире, так как отличительные его свойства находят множество применений.