Напряженно-деформированное состояние микрогеометрии различной геометрической формы при импульсном ударном нагружении

Детали изделий в процессе эксплуатации подвергаются многократному интенсивному ударному нагружению, параметры которого, как правило, не выводят интегральный объем материала из упругого состояния, но при этом ближайшие окрестности контактирующих поверхностей подвергаются локальному деформированию, в результате чего их геометрические параметры и механические свойства материалов в процессе эксплуатации значительно меняются (так называемое явление приработки) - и эти необходимо учитывать и закладывать в конструкцию на этапах проектирования и отработки. Существует много как конструктивных, так и технологических способов улучшения эксплуатационных характеристик деталей автоматики, направленных на целевое планирование комплекса свойств контактирующих поверхностей, формирующих, как правило, в их окрестностях внутренние напряжения противоположного по отношению к возникающим в процессе ее эксплуатации знака и тем самым повышающим усталостную прочность деталей и уменьшающим длительность периода приработки. При этом в формирование такого поля внутренних напряжений вкладывается в буквальном смысле значительная энергия и материальные средства [1, с. 185].

Сказанное позволяет сделать вывод о необходимости разработки модели, достоверно прогнозирующей кинетику изменения параметров, характеризующих приработку контактирующих поверхностей в процессе эксплуатации.

Теоретическое моделирование процесса импульсного нагружения микронеровности ударом проводилось с учетом изменения площади поперечного сечения крешерных элементов (рисунок 1) [2, с. 208]. Для микронеровности полная система уравнений, описывающая напряженно-деформированное и кинематическое состояние материала в рамках гипотезы плоских сечений для случая ударного нагружения падающей жесткой массой имеет вид [3, 1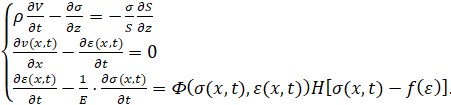1]:

             (1)

где: ρ - плотность материала стержня (принимается постоянной в процессе деформирования); σ и V - напряжение и скорость частиц стержня в поперечном сечении с координатой х в момент времени t соответственно; Нξ - единичная функция Хевисайда, отражающая упругий характер разгрузки; f(ε) - функция, аппроксимирующая диаграмму статического нагружения.

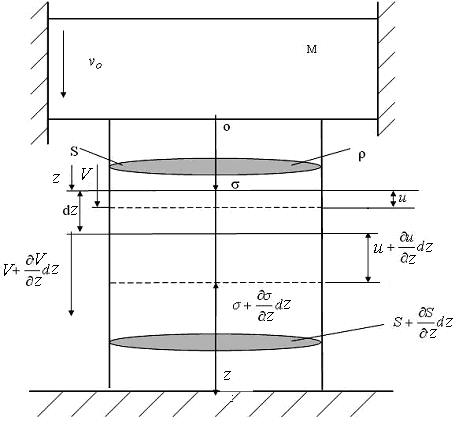
а)

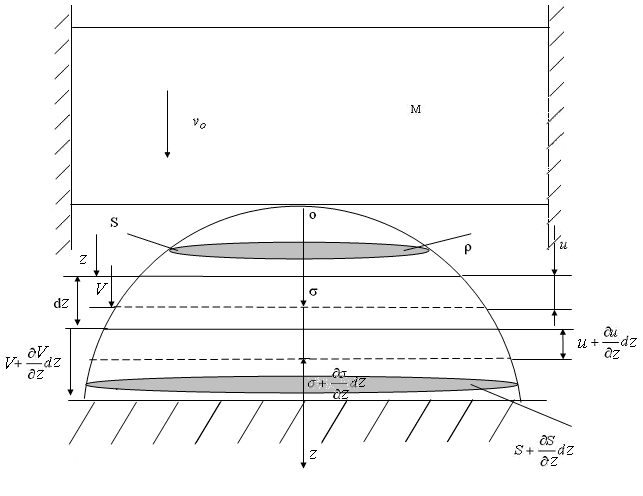
б)

Рис. 1. Микронеровность: а) цилиндрической формы; б) сферической формы

Анализ результатов при циклическом ударном нагружении единичной микронеровности цилиндрической формы проводился при следующих начальных условиях: материал – Медь М2; масса деформирующего элемента – М = 0,002 кг; высота микронеровности: – Н = 0,4 мм; напряжение на торце микронеровности – от 350 до 650 Н/мм²; площадь поперечного сечения: – S = 0,008 мм².

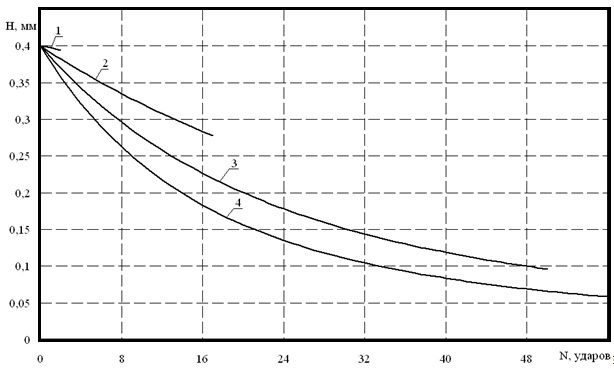
Рис. 2. Изменение высоты микронеровности цилиндрической формы при циклическом ударном нагружении

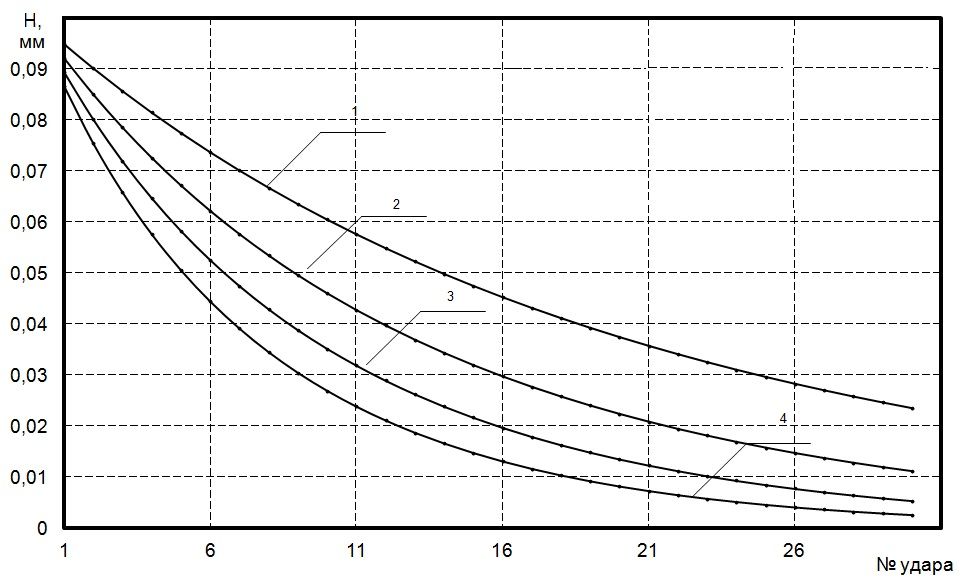
Рис. 3. Изменение высоты микронеровности сферической формы при циклическом ударном нагружении

На рис. 2 представлено изменение микронеровности цилиндрической формы при различных начальных условиях – линия 1 напряжение на торце микронеровности 350 Н/мм²; линия 2 – 450 Н/мм²; линия 3 – 550 Н/мм²; линия 4 – 650 Н/мм².

Анализ результатов при циклическом ударном нагружении единичной микронеровности сферической формы проводился при следующих начальных условиях: материал – Медь М2; масса деформирующего элемента – М = 0,002 кг; радиус микронеровности: R = 0,1 мм; напряжение на торце микронеровности – от 600 до 1500 Н/мм².

На рис. 3 представлено изменение микронеровности сферической формы при различных начальных условиях – линия 1 напряжение на торце микронеровности 600 Н/мм²; линия 2 – 900 Н/мм²; линия 3 – 1200 Н/мм²; линия 4 – 1500 Н/мм².

Предложенная модель процесса изменения геометрических параметров микронеровностей различной формы при ударном нагружении может использоваться для прогнозирования поведения микронеровности при различных начальных условиях.