Возможность понижения порядка в дифференциальном уравнении является одним из видов уравнений в полных дифференциалах. Пусть нам задано обыкновенное дифференциальное уравнение второго порядка:
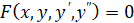. (1)
Определение. Если существует такая функция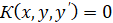 
в рассматриваемой области и имеет место равенство:
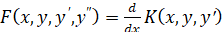, (2)
тогда уравнение (1) называют уравнением в полных дифференциалах.
Если уравнение (1) является уравнением в полных дифференциалах, тогда на основе равенства (2) можно записать
.
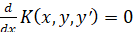Интегрируя это равенство, получим дифференциальное уравнение первого порядка:
.
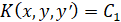В некоторых уравнениях (1) не выполняются условие полного дифференциала, тогда найдётся такая функция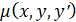 
, что после умножения на данное уравнение это уравнение будет удовлетворять условию полного дифференциала. В таком случае, функция 
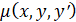называется интегрирующим множителем.
Однако, нужно уточнить, что не для каждого дифференциального уравнения будет существовать интегрирующий множитель.
Приведём примеры, где используется интегрирующий множитель для дифференциального уравнения второго порядка:
Пример 1. Найти решение для уравнения: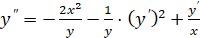 
Программа Maple
Для определения данного уравнения, необходимо выполнять последовательно все команды:
restart; with(DEtools): PDEtools [declare] (y(x), prime=x);
Запишем уравнение в полных дифференциалах второго порядка с помощью программы Maple в виде:
>ODE2:=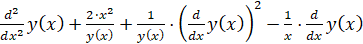
;
Уравнение выглядит ODE2:=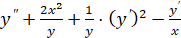
.
Чтобы определить интегрирующий множитель для данного уравнения, введём команду intfactor [2, с.75]:
>mu:=intfactor(ODE2);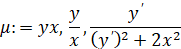 
Отдельное определение интегрирующих множителей:
>mu1:=mu[1]; mu2:=mu[2]; mu3:=mu[3];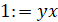 
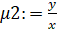
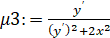
Первый интегрирующий множитель умножаем на данное уравнение, а затем определяем его тип:
>odeadvisor(mu[1]*ODE2);
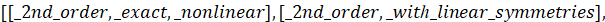
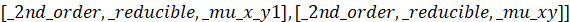
>R1:=firint(mu[1]*ODE2,y(x));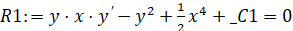 
а) нахождение интегрирующего множителя для новообразованного уравнения R1:
>muR1:=intfactor(R1);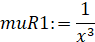 
б) понижение порядка в уравнении R1 с помощью первого интегрирующего множителя muR1, а также нахождение решения этого уравнения:
>R11:=firint(muR1*R1,y(x));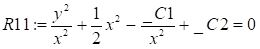 
>solve((R11, y(x));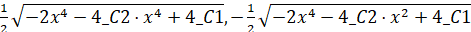 
.
Второй интегрирующий множитель умножаем на данное уравнение, а затем определяем его тип:
>R2:=firint(mu[2]*ODE2,y(x));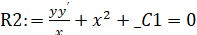 
а) нахождение интегрирующего множителя для новообразованного уравнения R2:
>mu:=intfactor(R2); muR2:=x.
б) понижение порядка в уравнении R2 с помощью второго интегрирующего множителя muR2, а также нахождение решения этого уравнения:
>R22:=firint(muR2*R2,y(x));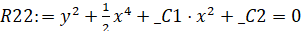 
>solve(R22, y(x));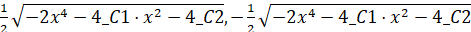 
.
>R3:=firint(mu[3]*ODE2, y(x));
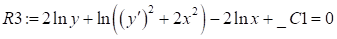
Для данного уравнения не существует общее решение.
Пример 2. Найти решение для уравнения: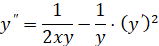 
Программа Maple
Для определения данного уравнения, необходимо выполнять последовательно все команды:
restart; with(DEtools): PDEtools [declare] (y(x), prime=x);
Запишем уравнение в полных дифференциалах второго порядка с помощью программы Maple в виде:
>ODE2:=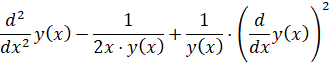 
Уравнение выглядит ODE2:=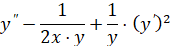
.
Чтобы определить интегрирующий множитель для данного уравнения, введём команду intfactor [2, с. 75].
Определение интегрирующего множителя для заданного уравнения:
>mu:=intfactor(ODE2); μ:=y,xy
Отдельное определение интегрирующих множителей:
>mu1:=mu[1]; mu2:=mu[2]; μ1:=y μ2:=xy
Первый интегрирующий множитель умножаем на данное уравнение, а затем определяем его тип:
>odeadvisor(mu[1]*ODE2);
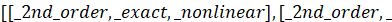
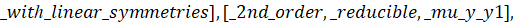
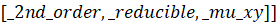
>R1:=firint(mu[1]*ODE2,y(x));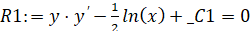 
а) нахождение интегрирующего множителя для новообразованного уравнения R1:
>muR1:=intfactor(R1); muR1:=1
то есть уравнение R1 удовлетворяет условию для полного дифференциала, поэтому не существует интегрирующий множитель [1, с. 33].
б) понижение порядка в уравнении R1 с помощью первого интегрирующего множителя muR2, а также нахождение решения этого уравнения:
>R11:=firint(muR1*R1,y(x));
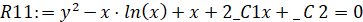
>solve(R11,y(x));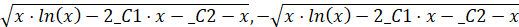 
.
Второй интегрирующий множитель умножаем на данное уравнение, а затем определяем его тип:
>R2:=firint(mu[2]*ODE2,y(x));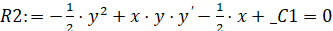 
а) нахождение интегрирующего множителя для новообразованного уравнения R2:
>muR2:=intfactor(R2);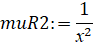 
б) понижение порядка в уравнении R2 с помощью второго интегрирующего множителя muR2, а также нахождение решения этого уравнения:
>R22:=firint(muR2*R2,y(x));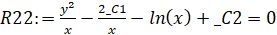 
>solve(R22,y(x));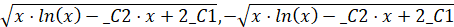 
.
.png&w=640&q=75)
