Анализ функционалов, заданных на выборках из нестационарного временного ряда

Во многих задачах прикладного статистического анализа существует необходимость тестирования тех или иных индикаторов локального поведения временного ряда с целью оценки вероятности их правильного срабатывания. Индикаторы представляют собой функционалы от фрагментов траектории случайного процесса. Примеры индикаторов: отношение числа положительных приростов значений временного ряда к числу отрицательных за определенный период времени; угловой коэффициент прямой регрессии для выборки заданной длины; расстояние между выборочными плотностями функции распределения ряда в той или иной норме, дисперсия накопленного размаха за определенный период и т.п.

Чтобы оценить эмпирическую условную вероятность того, что определенный интервал значений индикатора отвечает ожидаемому исследователем поведению ряда в настоящем или будущем, нужно иметь много реализаций изучаемого процесса, тогда как в наличии имеется лишь одна фактически наблюденная траектория. На практике берется фрагмент траектории, который представляется достаточно большим, и на нем собирается требуемая статистика. Но если временной ряд нестационарный, то, например, оптимизация длины выборки для получения минимальной ошибки индикатора по некоторому фрагменту прошлой траектории не имеет особого смысла, поскольку оптимум искался для конкретного фрагмента траектории случайного процесса. При другой последовательности тех же самых значений временного ряда возможен иной результат оптимизации. Возникает задача тестирования индикатора на устойчивость относительно различных реализаций случайного процесса, имеющего близкие выборочные распределения. Для этого требуется сгенерировать пучок возможных траекторий временного ряда, исходящий из заданного текущего состояния, и проверить на нем устойчивость срабатывания индикатора.

Для стационарного процесса набор траекторий может быть получен, если известна его функция распределения (ФР) F(x), которая предполагается непрерывной. Сначала генерируется произвольная последовательность чисел 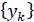, равномерно распределенных на [0;1], после чего по формуле

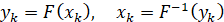
находятся элементы ряда 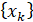, представляющего значения изучаемой случайной величины с заданной ФР.

Этот же подход можно применить и в том случае, если генеральная совокупность 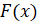 не известна, а оценивается по наблюдаемому временному ряду. Будем рассматривать случайные величины на отрезке  [0;1]. Разобьем этот отрезок на m классовых интервалов и определим эмпирические частоты 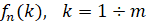попадания в них значений случайной величины по выборке заданной длины n. Для определенности предположим, что внутри классовых интервалов распределение равномерно. Тогда по этим вероятностям строится непрерывная выборочная функция распределения (ВФР), которая имеет вид

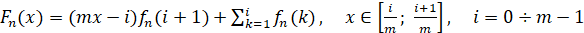  . (2)

Если же распределение нестационарно, то генеральной совокупности как таковой нет – в смысле сходимости к ней ВФР при увеличении длины выборки. Предлагаемый в работе метод генерации нестационарного временного ряда опирается на моделирование выборочной функции распределения приростов значений ряда в каждый момент времени, которая трактуется как локальная генеральная совокупность.

Рассматривается исходный временной ряд ξ(t)  и составляется ряд приращений

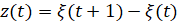  , (3)

который нормируется на отрезок [0;1]. Получившиеся числа обозначаются далее как :

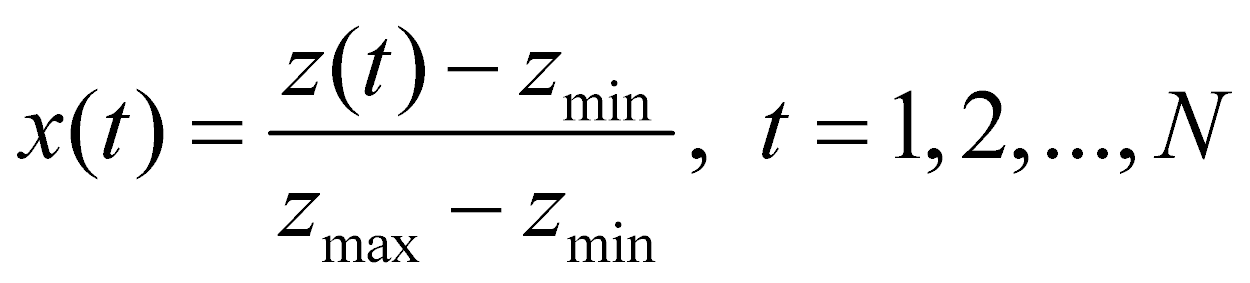. (4)

После этого весь имеющийся массив из N данных разбивается на 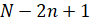встык-выборок длины n. Для каждой выборки длины n на шаге  строится выборочная плотность функции распределения (ВПФР) 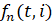. Для этого промежуток [0;1] делится равномерно на количество  интервалов, мелкость которых определяется в соответствии с методикой [1, 2]. Число промежутков разбиения должно быть определенным образом согласовано с эмпирическим распределением, представляемым в виде гистограммы. Оптимальное число классовых интервалов определяется как ближайшее целое к решению уравнения относительно m как функции от n:

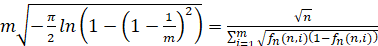  . (5)

Для каждой соседней пары встык-выборок определяются расстояния в норме L1 по формуле

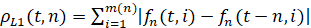. (6)

Для расстояний (6) строится согласованный уровень стационарности (СУС), представляющий однопараметрическую статистику, зависящую от длины выборки n. Пусть 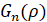 есть ВФР расстояний (6) между встык-выборками длины . Тогда в соответствии с работами [2, 3] согласованным уровнем стационарности называется величина 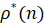, являющаяся решением уравнения

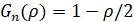. (7)

По найденному значению ρ*(n)  определяется индекс нестационарности 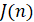 исходного временного ряда согласно [3]: это отношение СУС к теоретическому уровню стационарного статистического шума. В норме L1 шум определяется точностью построения гистограммы, т.е. равен 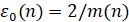, так что индекс нестационарности определяется формулой

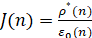. (8)

Разные ВПФР из одного и того же стационарного ряда отличаются одна от другой на величину 2/m(n)  с вероятностью 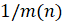 в соответствии с оптимальным разбиением гистограммы. Поэтому если 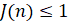, ряд считается

стационарным, а если J(n)>1 , то ряд нестационарный. Длина выборки  T, на которой плотности распределения, построенные в соседних окнах, различаются сильнее всего, называется основной длиной нестационарности ряда. Именно для выборок таких длин и ставится задача эволюции соответствующего выборочного распределения.

Пусть в каждый момент времени t∈ [t₀+1; t₀+T] по выборке длины T, отсчитанной назад от момента времени t , построены ВПФР fT(x,t)  и соответствующие ВФР F_T(x,t) по формуле (2). Если в каждый момент t>t₀  сгенерировать N значений случайной величины, распределенной с ВФР F_T(x,t), то получим  N траекторий нестационарной случайной величины, т.е. N реализаций выборки из временного ряда на промежутке [t₀+1;t₀+T] . Начальная точка для всех этих реализаций общая – это x(t₀). Задавая различные равномерно распределенные ряды ,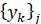_, где j=1,...,N есть номер генерации, можно получить пучок траекторий, ассоциированных с ВПФР текущих выборок. В каждый момент времени одна из возможных траекторий случайного процесса, для которого ВПФР меняется от начальной f_T(x,t₀) до конечной f_T(x,t₀+T), моделируется по формуле обращения соответствующей локальной по времени функции распределения, движущейся в скользящем окне длины T:

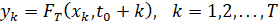. (9)

Подчеркнем, что, согласно (9), в каждый момент времени 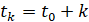 генерируется только одно значение ряда из распределения 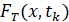. Эта методика была предложена в работе [4].

Каждая из траекторий пучка порождает на отрезке 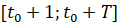 ВПФР 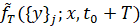, отличную, вообще говоря, от наблюденной 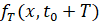. По совокупности сгенерированных траекторий можно оценить, насколько значимо отклонение этих распределений в норме L1 одно от другого и от фактической ВПФР 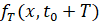. Предположительно все эти выборочные траектории являются реализациями некоторого неизвестного нестационарного распределения вероятностей. Моделирование ряда корректно, если траектории обладают свойствами: а) СУС попарных расстояний между сгенерированными выборками приблизительно равен 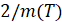; б) СУС попарных расстояний между сгенерированной и фактической ВПФР  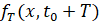в окне 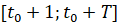 также примерно равен 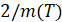; в) СУС расстояний между сгенерированной и фактической исходной ВПФР  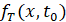примерно равен расстоянию между  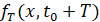и

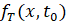
В работе [3] описанный метод применялся для ряда приростов цен закрытия 5-минутных интервалов для индекса RTS. Для данного ряда основная длина нестационарности равна T=8000, а уровень шума для нее равен 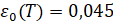. При тестировании оказалось, что согласованное расстояние между сгенерированными распределениями по выборкам длины T  на промежутке 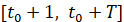, равно 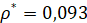, что близко к величине 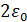. Такой же величине равно и согласованное расстояние между сгенерированными выборками и фактически наблюденной ВПФР 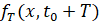. Расстояние между фактическими распределениями, разделенными временным промежутком длины T, в данном случае равно 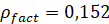. Этой же величине равен и СУС между исходной и сгенерированной выборками. Заметим, что СУС встык-выборок временного ряда приращений индекса РТС равен на этой длине величине 0,144. Поэтому можно считать, что эксперимент генерации нестационарного ряда в заданном классе распределений проведен корректно.

На сгенерированных траекториях можно провести тестирование какого-либо управляющего функционала. Пусть на выборке длины  задан некоторый функционал 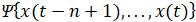. Обозначим  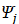значение функционала на j-ой сгенерированной траектории. Для анализа его статистических свойств строится распределение  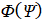и определяются среднее, дисперсия, нормированное среднее:

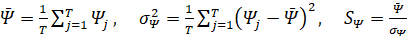  . (10)

Затем численно решается задача отыскания максимума среднего значения или нормированного среднего в зависимости от тех или иных параметров (если они есть), которыми определяется функционал из заданного семейства.

Покажем на простом примере, что тестирование функционала, называемого «доходностью торговой стратегии», на случайном пучке траекторий, типичных для выбранного инструмента, гораздо более отвечает реальности, чем тестирование пусть и на достаточно длинной, но единственной исторической реализации. Рассмотрим стратегию «следования за трендом» для торговли внутри одного торгового дня. Соответствующий отрезок 5-минутных данных составляет окно в 144 точки. Модельная тестируемая стратегия состоит в следующем. Имеющаяся историческая траектория делится на фрагменты длиной 144 точек. Внутри каждого фрагмента по выборке в скользящем окне 20 точек определяется наличие или отсутствие тренда. Если текущее состояние определено как трендовое, то в этот момент делается вход в соответствии с направлением тренда. Выход из позиции осуществляется по достижении заданного уровня прибыли – например, удвоенной комиссии, либо по стоп-сигналу минимизации убытка, либо по окончании фрагмента. Оптимизируемым параметром стратегии является уровень стоп-сигнала. Соответствующий график движения оптимальной доходности как функции времени приведен на рис. 1. Как видно, такая тривиальная стратегия не представляет интереса с практической точки зрения, но пример носит иллюстративный характер. Доля положительных сделок в области оптимизации параметра составила 0,5; средняя доходность на положительную сделку равна 0,0048, средний убыток на отрицательную сделку равен – 0,0043.

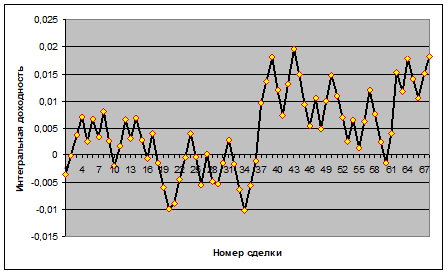
Рис. 1. Движение доходности в области оптимизации параметра

Выберем произвольный фрагмент ряда длиной 8000 из области, где проводилась оптимизация, протестируем на нем торговую систему и определим значение функционала доходности. В результате было получено распределение доходности, показанное на рис. 2 и отмеченное легендой «факт».

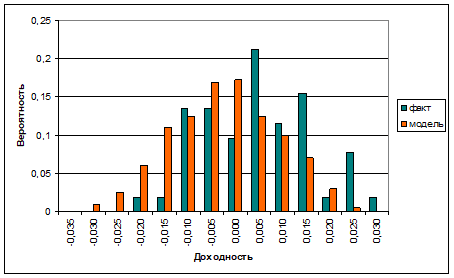
Рис. 2. Распределение доходностей

Среднее значение доходности за этот период составило 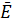=0,0022 при среднеквадратичном отклонении σ_E=0,011, так что коэффициент Шарпа равен S_T=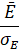= 0,20. В промежутке 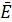±σ_E находится 58 % ожидаемых доходностей. В частности, за последний промежуток оптимизации   тыс. точек доходность оказалась равной 0,007. 

Запустим теперь эту оптимизированную стратегию на новом участке, где оптимизации не проводилось, т.е. на промежутке 32÷40 тыс. Обнаруживаем, что доходность системы на этом участке составила -0,004. Из распределения доходности (рис. 2, «факт») находим, что вероятность события «доходность на промежутке 8000 не более -0,004» составляет приблизительно 0,30. Чтобы составить более реальное представление о возможностях этой торговой модели, сгенерируем на промежутке 32÷40 тыс. 200 траекторий с тем же распределением приращений. На каждой из них запустим торговую систему и определим доходность. Соответствующее распределение также показано на рис. 2 (легенда «модель»). По этому распределению средняя доходность равна E'=-0,005, а среднеквадратичное отклонение равно σ_E'=0,013, так что коэффициент Шарпа равен S_T'=-0,38. Вероятность того, что доходность будет лежать в промежутке E'±σ_E', равна 0,80. Тем самым показано, что доходность на уровне -0,004 за 8000 шагов для этой модели вполне обычна. Вероятность же того, что доходность будет более 0,07, оказывается примерно равной 0,10. Такой результат получился вследствие того, что оптимизация была проведена на одной случайной траектории, и параметр, оптимальный для нее, не будет таковым на любой другой траектории с тем же распределением. Следовательно, более корректно проводить оптимизацию и тестирование не на одной исторической реализации, а на пучке траекторий с характерным для данного ряда нестационарным распределением.