Аналитическая модель конвективного акселерометра с внутренним источником тепла

Работа теплового (конвективного) акселерометра [1] основана на явлении конвекции газа в полости под действием внешних сил инерции. По сравнению с традиционными датчиками ускорения, тепловые акселерометры обладают высокой надежностью, низкой стоимостью, способностью выдерживать и измерять большие перегрузки. Прибор имеет нагревательный элемент, расположенный в замкнутой полости и создающий вокруг себя симметричное тепловое поле. С противоположных сторон этого элемента симметрично расположены датчики тепла. При отсутствии внешнего ускорения тепловые датчики Д1 и Д2 выдают одинаковый сигнал, и профиль температуры вдоль оси чувствительности симметричен относительно нагревателя (рис. 1,а). Под действием внешнего ускорения между датчиками возникает ненулевая разность температур dT, зависящая от амплитуды ускорения, и температурный профиль искажается (рис. 1,б). По этой разности оценивается искомое ускорение.

Расчет характеристик прибора требует решения двух- или трехмерной краевой задачи, описываемой системой дифференциальных уравнений Навье–Стокса, которая в общем случае может быть решена лишь численно с помощью конечно-разностных или конечно-элементных методов.

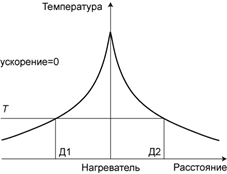
а

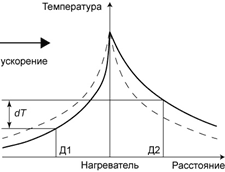
б

Рис. 1. Профиль температуры вдоль оси чувствительности прибора при нулевом (а) и ненулевом внешнем ускорении (б)

В то же время, простейшие одномерные модели физических процессов часто могут позволить на качественном уровне достаточно хорошо исследовать функционирование приборов. В работе [2] была построена модель на основе двух одномерных уравнений конвекции-диффузии в смежных областях, а тепловой источник представлялся в виде заданной постоянной температуры на общей границе. В настоящей работе представлена более адекватная с физической точки зрения модель одномерной конвекции-диффузии в стержне с внутренним источником тепла.

Пусть полость прибора имеет поперечное сечение в плоскости, перпендикулярной осям нагревательного элемента и датчиков, размерами 2L×H. Считаем, что на корпусе прибора поддерживается постоянная температура T_C. Если вертикальный размер полости мал по сравнению с горизонтальным (H<<2L), то, полагая пренебрежимо малыми величины производных температуры по «вертикальной» переменной y, получим одномерную модель конвективного теплопереноса:

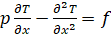,   (1)

где p=u/D – параметр отношения конвективной и диффузионной составляющих теплопереноса; u – «горизонтальная» составляющая скорости; D – коэффициент диффузии; T(x) – искомый продольный профиль температуры; f(x)  – функция внутреннего источника тепла.

Уравнение (1) дополним граничными условиями Дирихле:

T(-L)=T(L)=TC, (2)

Точное решение (1), (2) имеет вид

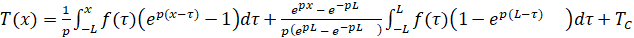.(3) 

В качестве примера представим функцию источника кубическим B‑сплайном с амплитудой Q и носителем suppf=(-a,a) (0<a<L). Графики температуры (3) в зависимости от p показаны на рис. 2 (при L=1 , a=0,1L,Q=100). При значениях p<1 преобладает влияние диффузионной составляющей, а при p>1 более существенный вклад оказывает конвекция. При очень больших значениях величины линейной скорости u, когда p>>1, температура остается близкой к T_C вплоть до достижения ближайшей окрестности источника (x=±a ), где возникает пограничный слой и наблюдается ее резкий рост.

Одной из главных проблем при проектировании теплового акселерометра является нахождение оптимального расстояния между датчиками и нагревательным элементом. Для повышения чувствительности прибора необходимо добиться максимального изменения температуры на датчиках в расчете на единицу ускорения. Запишем выражения для разности температур между каждым из симметрично расположенных датчиков и нагревательным элементом:

dT(x)=T(x)-T(-x), (4)

и приравняем ее производную к нулю:

dT_x'=0 .

В итоге находим, что максимум разности (4) достигается в точке .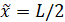

График dT(x)  для p=4 приведен на рис. 3.

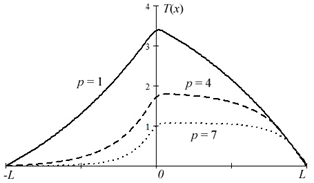
Рис. 2. Точные решения уравнения (1) с краевыми условиями (2) при различных значениях параметра p

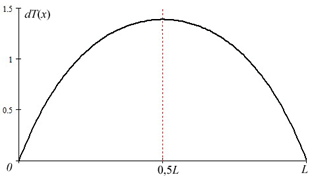
Рис. 3. Разность температур в противоположных точках как функция расстояния до нагревателя

Полученные результаты на качественном уровне хорошо согласуются и подтверждают результаты [2], однако являются более адекватными с количественной точки зрения, учитывая тот факт, что в качестве рабочей характеристики прибора как правило выступает не температура нагревателя, K, а его мощность, Вт.