Для решения прикладных и математических задач в настоящее время существуют различные программы, с помощью которых можно довольно быстро вычислить сложные вычисления. К таким программам можно отнести MATCAD, MACHCAD, MATLAB, MAPLE и другие.
К прикладным задачам можно отнести условие, при котором допущено что дан тонкий однородный стержень 0<x<l, боковая поверхность которого теплоизолированная. Необходимо найти распределение температуры u(x,t) в стержне, если концы стержня поддерживаются при нулевой температуре,
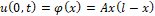
Решение поставленной задачи сводится к решению смешанной (начально-краевой) задачи для уравнения теплопроводности, которое относится к уравнениям параболического типа.
Команда restart очищает значение всех переменных.
> restart:
Задаем уравнение теплопроводности:
>eq:=diff(u(x,t),t)-a^2*(diff(u(x,t),x$2))=0; 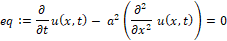
где u(x,t) эта температура стержня в точке x в момент времени t, a связано с коэффициентами теплоемкости и теплопроводности.
Уравнение заносится в переменную eq для того, чтобы в дальнейшем можно было сослаться на эту переменную в своих вычислениях. При этом мы используем знак присвоения ":=". Если использовать двоеточие после команды – Maple выполнит ее, но не покажет результат. Это бывает удобно, когда много мелких команд.
Для выделения единственного решения уравнения теплопроводности необходимо к уравнению присоединить начальные и граничные условия. Для задач этого типа задается только одно начальное условие, а именно, температура в начальный момент времени.
> InitC:=u(x,0)=phi(x); 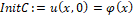
> phi:=x->A*x(l-x);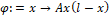
> BoundC:=u(0,t)=0,u(l,t)=0; 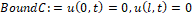
Получим решение методом разделения переменных. Для решения уравнения в частных производных имеются команда pdsolve и набор команд пакета PDEtools. Обращение к команде имеет следующий вид: pdsolve(PDE,FUN,OPT), где PDE уравнение, FUN неизвестная функция, а OPT дополнительные параметры.
Ответ может быть представлен специальной структурой PDESolStruc, которая содержит термин &where и состоит из двух полей: функционального представления и перечня обыкновенных дифференциальных уравнений, полученных в результате процедуры разделения переменных. Данная структура предназначена для указания возможных решений.
Решение при этом может быть получено с помощью команды build из пакета PDEtools. В качестве дополнительных параметров OPT могут использоваться: указание на возможную форму решения HINT=HI, параметр INTEGRATE, означающий автоматическое интегрирование получающейся системы обыкновенных дифференциальных уравнений, указание на поиск явного решения build. В качестве HI могут стоять знаки суммы и произведения или алгебраическое выражение. Уравнения могут быть заданы непосредственно в теле команды.
> res:=pdsolve(eq,HINT=X(x)*T(t)); 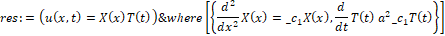
При решении нас интересуют два уравнения, которые находятся в квадратных скобках. Извлечь конкретный элемент или несколько элементов из уравнения можно с помощью команды op (i, struc), гдеstruc структура данных из которой нужно извлечь выражение, а i целое число.
> res1:=op(2,res); 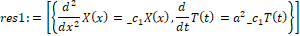
> eq1:=op(1,res1[1]); 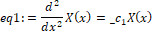
Хорошо известно, что физически осмысленные решения получаются при выборе отрицательной константы разделения. Теперь нужно сделать замену переменной _c1=-λ. Замену переменной можно провести в ручную, либо воспользовавшись командой subs, структура которой следующая: subs(x=a,EXPR), где x и а заменяемые переменные, а EXPR выражение, в котором происходит замена.
> eq1:=subs(_c[1]=-lambda,eq1); 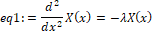
Введем ограничение переменной λ, которая должна быть больше "0", для этого воспользуемся командой assume()
> assume(lambda>0);
Для аналитического и численного решения обыкновенных дифференциальных уравнений используется команда dsolve, причем во всех случаях используется единый формат команды: dsolve(ODE,VAR,OPT). Для решения задачи Коши в уравнения ODE нужно включить так же начальные условия, а для краевой задачи соответственно краевые условия.
> s1:=dsolve(eq1); 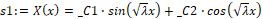
Для того, чтобы преобразовать наше уравнение в функцию можно воспользоваться командой unapply:
> X:=unapply(rhs(s1),x); 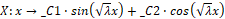
Найдем постоянные С1 и С2 из начальных условий:
> e1:=X(0)=0; e1:=_C2=0
> e2:=X(l)=0; 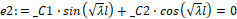
Составим систему из полученных уравнений:
> sistem:={e1,e2}; 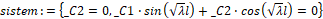 .
.
Запишем матрицу коэффициентов системы при помощи linalg[genmatrix]
> with(linalg):
> M:=genmatrix(sistem,[_C1,_C2]);
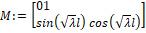
Вычислим определитель при помощи linarg[det](имя матрицы).
> Delta:=det(M); 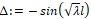
Для получения всех решений уравнений, содержащих периодические функции, следует присвоить переменной _EnvAllSolutions значение true. В противном случае, по умолчанию функция solve выдаст только одно решение. При помощи команды solve решим полученное выражение относительно λ.
> _EnvAllSolutions:=true:solve(Delta,lambda); 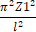
Заменим Z1=k для удобочитаемости формулы, символ "%" означает предыдущую строку
> subs(_Z2=k,%); 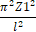
> ev:=unapply(%,k); 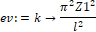
Если нужно вновь использовать переменную так, будто раньше ее никак не использовали (т.е. освободить ее для значений любого типа), присвоим ей ее имя в одинарных кавычках.
> X:='X'; X:=X
Ограничим значение переменной k и заменим переменную λ в уравнении eq1 на функцию ev(k):
> assume(k,posint);
> ur:=subs(lambda=ev(k),eq1); 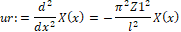
Решим уравнение ur при помощи команды dsolve:
> ur:=dsolve({ur,X(0)=0,X(l)=0},X(x)); 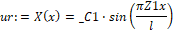
> ef:=unapply(rhs(ur),(k,x)); 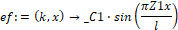
Возьмем второе уравнение из уравнения res1:
> eq2:=op(2,res1[1]); 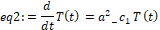
Заменим _c1 на -ev(k) в уравнении eq2
> eq2:=subs(_c[1]=-ev(k),eq2);
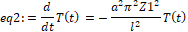
Решим уравнение eq2 при помощи команды dsolve:
> eq2:=dsolve(eq2,T(t));
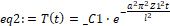
Поскольку константа _C1 входит в решение только в виде произведений _C1⋅_C2, _C1⋅_C3, можно сократить количество констант присвоив _C1 значение 1.
> C1:=1:eq2; 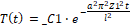
Общее решение уравнения представляет из себя линейную комбинацию всех частных решений.
> u:=(x,t)->sum(C[k]*exp(-ev(k)*a^2*t)*ef(k,x),k=1..n);
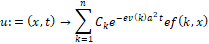
> u(x,t);
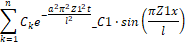
Из начального условия найдем неизвестные коэффициенты
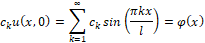
Получили разложение функции φx в ряд Фурье по синусам. Вычислим коэффициенты разложения:
> assume(l>0);
> C[k]:=simplify((2/l)*int(sin(Pi*k*x/l)*phi(x),x=0..l));
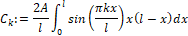
Используя предложенную методику решения, можно вычислить другие подобные физические, технические и математические прикладные задачи.

.png&w=640&q=75)