Пусть Ω – конечная односвязная область плоскости xOy, ограниченная отрезками
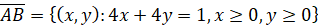 ,
,
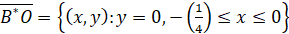 ,
,
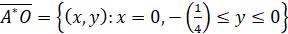 ,
,
и дугами
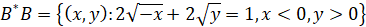 ,
,
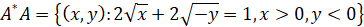 ,
,
а
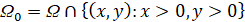 ,
,
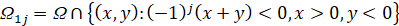 ,
,
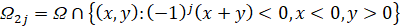 ,
, 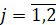 .
.
В области Ω рассмотрим уравнение
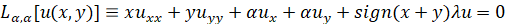 , (1)
, (1)
здесь α – заданное число, причем, 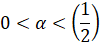 , а λ – параметр.
, а λ – параметр.
Задача. Найти значения параметра λ и соответствующие им нетривиальные в  функции
функции 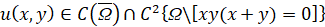 , удовлетворяющие уравнению (1) в области
, удовлетворяющие уравнению (1) в области 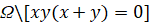 и условиям
и условиям
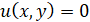 ,
, 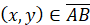 ; (2)
; (2)
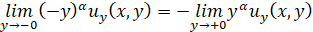 ,
, 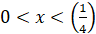 ; (3)
; (3)
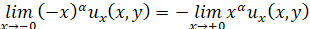 ,
, 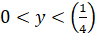 ; (4)
; (4)
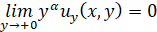 ,
, 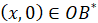 ;
; 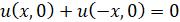 ,
, 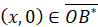 ; (5)
; (5)
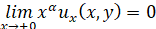 ,
, 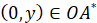 ;
; 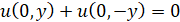 ,
,  . (6)
. (6)
Считая λ≠0, нетривиальные в области 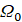 решения
решения 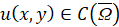 задачи ищем в виде
задачи ищем в виде 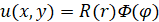 , где
, где 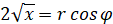 ,
, 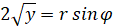 ,
, 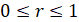 ,
, 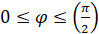 . Тогда, из (1) получим уравнения
. Тогда, из (1) получим уравнения
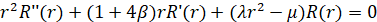 ,
, 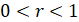 ; (7)
; (7)
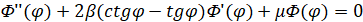 ,
, 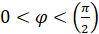 , (8)
, (8)
где 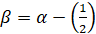 , а μ – константа разделения.
, а μ – константа разделения.
Пользуясь общими решениями уравнений (7) и (8), находим, что нетривиальные и непрерывные в 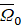 решения уравнения (1) имеют вид [1]
решения уравнения (1) имеют вид [1]
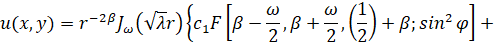
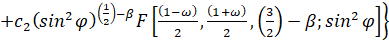 , (9)
, (9)
где 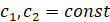 ,
, 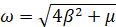 ,
, 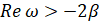 ,
, 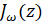 – функция Бесселя первого рода, F(a,b,c;z)
– функция Бесселя первого рода, F(a,b,c;z)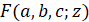 - гипергеометрическая функция Гаусса.
- гипергеометрическая функция Гаусса.
Из (9) следует, что
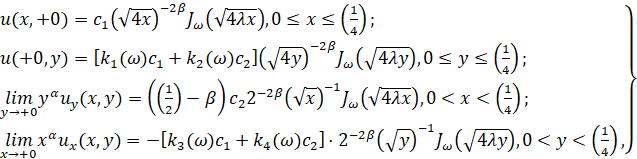 (10)
(10)
где 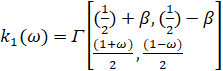 ,
, 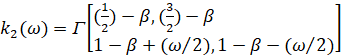 ,
,
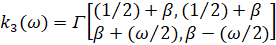 ,
, 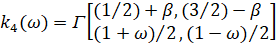 .
.
В области 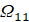 введем в рассмотрение функцию
введем в рассмотрение функцию
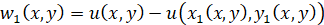 , (11)
, (11)
где 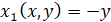 ,
, 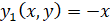 . Если
. Если 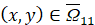 ,
, 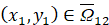 . Функция
. Функция 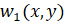 удовлетворяет условиям
удовлетворяет условиям 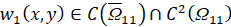 ,
,
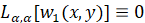 ,
, 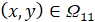 ,
, 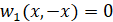 ,
, 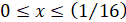 . (12)
. (12)
Производя замену 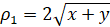 ,
, 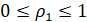 ;
;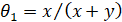 ,
, 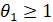 и применяя метод разделения переменных
и применяя метод разделения переменных 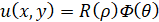 , находим решения задачи (12) в области Ω11:
, находим решения задачи (12) в области Ω11:
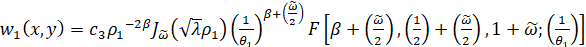 ,
, 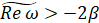 .
.
Отсюда, в силу обозначения (11) и условий (3), (6), имеем
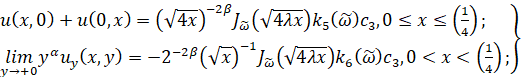 (13)
(13)
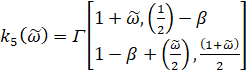 ,
, 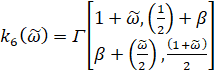 .
.
Аналогично, используя условиям (4), (5), получим соотношения:
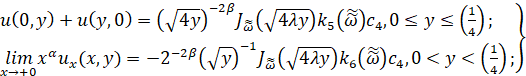 (14)
(14)
Подставляя (10) в (13), (14) и полагая 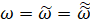 , находим
, находим
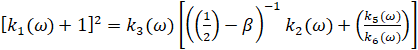 , (15)
, (15)
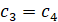 ,
, 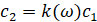 ,
, 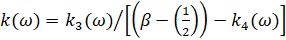 . (16)
. (16)
Подставляя выражение 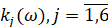 в равенство (15), получим уравнение
в равенство (15), получим уравнение 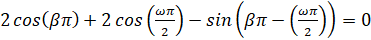 . Решениями этого уравнения, удовлетворяющими условию
. Решениями этого уравнения, удовлетворяющими условию 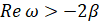 , являются числа
, являются числа 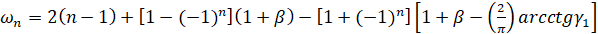 , n∈N, где
, n∈N, где 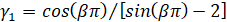 .
.
Подставляя в (11) 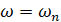 и
и 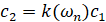 , а затем, удовлетворяя условию
, а затем, удовлетворяя условию 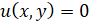 ,
, 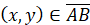 , получим
, получим 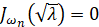 , n∈N.
, n∈N.
Известно, что 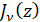 при ν>-1 имеет только действительные корни. Обозначая через
при ν>-1 имеет только действительные корни. Обозначая через 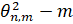 -ный положительный корень уравнения
-ный положительный корень уравнения 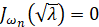 , находим собственные значения
, находим собственные значения 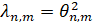 , n,m∈N задачи и соответствующие им собственные функции в области
, n,m∈N задачи и соответствующие им собственные функции в области 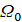 :
:
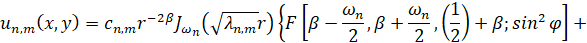
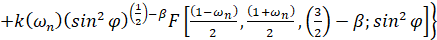 ,
, 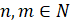 ,
,
где 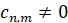 – произвольные постоянные, а
– произвольные постоянные, а 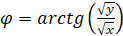 .
.
Аналогично, исследуется задача, в том случае, когда (5), (6) заменены условиями 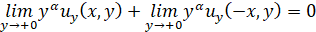 ,
, 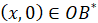 ;
; 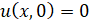 ,
, 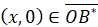 и
и 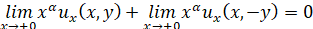 ,
, 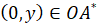 ;
; 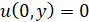 ,
, 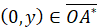 . При этом
. При этом 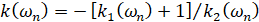 ,
, 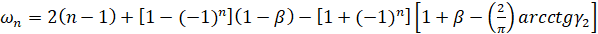 ,
, 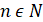 , где
, где 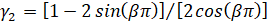 .
.
Собственные функции этих двух задач в областях гиперболичности уравнения (1) находятся как решения видоизменённой задачи Коши для уравнения (1) [2].

.png&w=640&q=75)