ВВЕДЕНИЕ
Бедственное состояние современного гражданского воздушного флота объясняется низкой, на грани убыточности, рентабельностью пассажирских судов гражданской авиации.
Низкая рентабельность воздушных судов объясняется нерационально большим объемом потребляемого топлива при современной, дозвуковой крейсерской скорости полета.
Доля затрат на топливо в общих затратах на транспортные услуги настолько велика, что часто не покрывает понесенные затраты на эти услуги.
По исследованиям причин банкротств, приведенным в СМИ, за первое полугодие 2014 года рентабельность 41 крупнейших авиакомпаний была отрицательной и составила минус два процента, авиакомпании работали в убыток, когда прибыль компаний оказалась меньше понесенных ими затрат на услуги.
Согласно статистическим данным, к 2018 году прекратили работу 20 авиакомпаний, наиболее резонансными из которых стало банкротство Вим-Авиа, затронувшее 196000 пассажиров.
Причина краха авиакомпаний – не стоимость топлива и падение спроса на авиаперевозки, как часто объясняют причину банкротств, а несовершенство воздушных судов по потреблению топлива.
Создание транспортной техники гражданской авиации на принципиально новых, физических законах движения в воздушной среде с природо-подобной техникой движения, присущей дельфинам, может избавить экономику от налогового бремени содержания гражданской авиации в виде дотаций и субсидий.
Высокорентабельные авиалайнеры со сверхзвуковой скоростью полета, при современных двигателях и потреблении топлива, откроют новую эру воздухоплавания, эру движения в воздухе без лобового сопротивления и звукового удара.
Новый тип авиалайнеров с семикратно увеличенной рентабельностью обеспечит снижение потребительских цен на авиабилеты не только в районы Дальнего Востока и Крайнего Севера, но и по всей стране.
I. ГЛАВНЫЕ АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
1. ЭНЕРГИЯ ПОТОКА
Корпускулярно-волновая концепция микрочастиц [2, §2.1], представляет молекулу жидкости не в виде шарообразной частицы-корпускулы, а в виде сферического объема пространства, который приходится на долю одной молекулы в объеме сосуда с жидкостью. Молекула жидкости находится внутри этого объема, удерживая его от «захлопывания» окружающими молекулами кинетической энергией своего теплового движения. Двигаясь внутри объема по спирально-сферической траектории, молекула успевает оттолкнуть все соседние молекулы, стремящиеся проникнуть в ее объем колебания.
Дискретный характер движения жидкостей [2, §4], когда в потоке молекулы движутся не одновременно и непрерывно в направлении падения давления, а перемещаются в виде поочередных перескакиваний, объясняет причину расширенного состояния потока жидкости.
В состоянии поступательного перескока молекула движется без своего объема, не занимая собой объема потока, перемещаясь по объемам колебаний покоящихся молекул, дифрагируя с ними, огибая их и не вступая в столкновение.
Срываясь из состояния покоя в состояние поступательного перескока, молекула освобождает собственный объем колебания, который заполняется соседними молекулами, расширяя собственные объемы колебаний за счет освободившегося объема.
В результате, работа расширения потока жидкости динамическим давлением в потоке равна
\( A = \rho \upsilon^{2}\omega l\); (1.1)
где \( \rho \upsilon^{2}\) – динамическое давление в потоке жидкости;
\( \rho\) – плотность жидкости;
\( \upsilon\) – скорость течения потока;
\( \omega ;l\) – соответственно, площадь сечения потока и длина.
В момент времени, когда кинетическая энергия перескока молекулы становится соизмеримой с кинетической энергией теплового колебания, происходит ударное столкновение перескакиваемой молекулы с любой из покоящихся на направлении перескока.
Завершая процесс перескока, молекула оказывается зажатой, защемленной между объемами колебаний покоящихся молекул, не обладая собственным объемом колебаний.
Обладая скоростью перескока, защемленная молекула расталкивает зажавшие ее окружающие молекулы, освобождая себе объем колебания за счет сжатия объемов соседних молекул. Деформация сжатия при расталкивании распространяется по объему потока со скоростью звука в жидкости.
Работа сжатия потока определяется ударным давлением в жидкости и равна
\( A_{сж} = \rho a\upsilon \omega l\); (1.2)
где \( \rho a\upsilon\) – ударное давление в потоке жидкости;
\( a\) – скорость звука по жидкости.
Как нетрудно заметить при составлении уравнения полной энергии потока, работа сжатия потока по (1.2) и работа расширения динамическим давлением по (1.1) должны суммироваться с разными знаками, так как в движущемся потоке энергия ударного давления сжимает поток, а энергия динамического давления его расширяет.
Полная энергия потока в его естественном состоянии равна
\( U_{1} = A_{сж} - A_{расш} = \rho a\upsilon \omega l - \rho \upsilon^{2}\omega l\); (1.3)
Полная энергия потока в момент его внезапной остановки и сжатия на объем $\omega \Delta l$, равна
\( U_{2} = \rho a\upsilon \omega (l - \Delta l) - \rho \upsilon^{2}\omega (l - \Delta l)\); (1.4)
\( \Delta l\) – деформация сжатия потока при его внезапной остановке.
Энергия давления, воспринимаемая ограничивающими поток поверхностями, определяется разностью (1.3) и (1.4), после вычитания равна
\( U_{уд} = U_{1} - U_{2} = \rho a\upsilon (1 -\frac{\upsilon }{a})\Delta l\omega\); (1.5)
Как следует из (1.5), энергия, выделяемая потоком жидкости при его внезапной остановке, определена не динамическим давлением потока, а ударным давлением.
2. СИЛА НОРМАЛЬНОГО ДАВЛЕНИЯ СТРУИ
На рисунке 1 показана плоская пластинка площадью $h⋅b$, движущаяся вместе с потоком жидкости со скоростью $\upsilon$, относительная скорость движения пластинки и потока жидкости равна нулю.

Рис. 1. Набегание струи на пластинку
С момента мгновенной остановки пластинки в потоке жидкости за время $T$ через нее пройдет, ударившись о ее поверхность, струя потока жидкости длиной $l$ и площадью сечения h⋅b, равной площади сечения пластинки. При этом работа внутренней силы $F_{дин}$, действующей у пластинки, равна:
\(A_{дин} = F_{дин}l\); (2.1)
Объем энергии, выделяемый из потока при его остановке, не зависит от способа его остановки, ударного, как получено в (1.5) или растянутого во времени при прохождении потока через пластинку на рисунке 1. Поэтому приравняем работу силы динамического давления потока на пластинку (2.1) энергии, выделяемой потоком при его остановке по (1.5)
\( F_{дин}l = \rho a\upsilon (1 -\frac{\upsilon }{a})\Delta l\omega\); (2.2)
Из (2.2) сила давления струи потока на пластинку определяется в виде
\( F_{дин} = \rho a\upsilon (1 -\frac{\upsilon }{a})\frac{\Delta l}{l}\omega\); (2.3)
Учитывая, что мгновенный удар потока (1.5) растянут во времени $T$, а закон Гука позволяет принять отношение $\frac{\Delta l}{l} =\frac{\upsilon }{a}$, то сила внутреннего давления струи потока на плоскую пластинку определяется в виде
\( F_{дин} = \rho a\upsilon (1 -\frac{\upsilon }{a})\frac{\upsilon }{a}\omega\); (2.4)
Так как величина внешней силы давления потока, силы скоростного напора, по величине равна половине силы динамического давления, то, разделив пополам (2.4), получим внешнюю силу давления струи, приложенную нормально к пластинке.
\( F_{N} =\frac{1}{2}\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\omega\); (2.5)
Формулой (2.5) получено выражение силы давления струи потока жидкости на плоскую пластинку.
В этой формуле скобками представлена зависимость коэффициента нормального давления струи потока в виде
\( C_{N} = (1 -\frac{\upsilon }{a})\); (2.6)
При движении воды ее скорость υ значительно отличается от скорости звука в воде $a = 1435\ {м}/{с}$, поэтому для воды коэффициент $C_{N}$ мало отличается от единицы.
3. ПОДЪЕМНАЯ СИЛА И СИЛА ЛОБОВОГО СОПРОТИВЛЕНИЯ
Поместив плоскую пластинку в поток жидкости под углом $\alpha$ к вектору скорости потока $\upsilon$ (рис.2), и зная величину внешнего нормального давления струи по (2.5) при $\alpha = 90^{\circ}$, можно легко доказать и записать выражение силы, приложенной нормально к поверхности пластинки в виде (3.1).
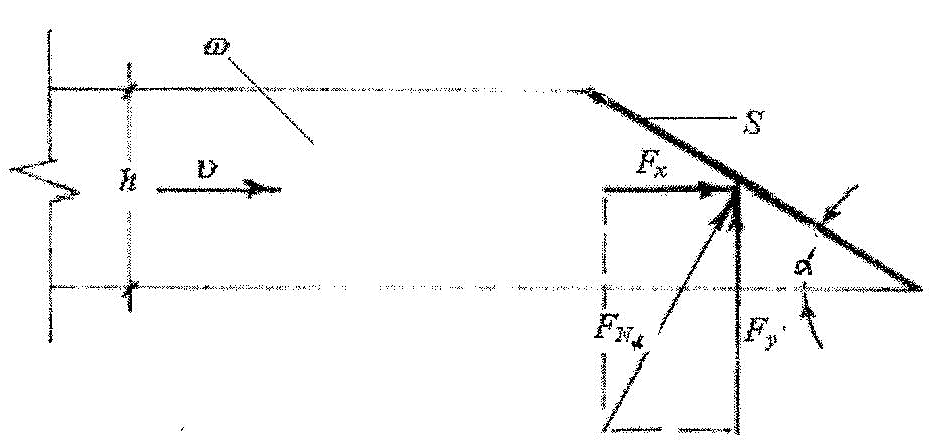
Рис. 2. Силы воздействия потока на пластинку с углом атаки α
\( F_{N_{\alpha }} = F_{N_{90^{\circ} }}\sin \alpha\); (3.1)
Очевидно, что подъемная сила, действующая на пластинку, равна проекции силы FNα на вертикальную ось.
\( F_{y} = F_{90}\sin \alpha \cos \alpha\); (3.2)
Сила лобового давления воды на пластинку равна проекции силы $F_{N_{\alpha }}$ на горизонтальную ось. Взятая с обратным знаком, эта сила является силой лобового сопротивления пластинки – $F_{x}$.
\( F_{x} = F_{N_{\alpha }}\sin^{2}\alpha\); (3.3)
Подставляя в (3.2) и (3.3) $F_{N_{90^{\circ} }}$ по (2.5) и учитывая, что площадь поверхности пластинки под углом $\alpha = 90^{\circ}$ равна
\( \omega = S⋅\sin \alpha\); (3.4)
где $S$ – площадь поверхности пластинки под углом $\alpha$, выражения подъемной силы и силы лобового сопротивления для пластинки с углом атаки $\alpha$ окончательно примут вид:
\( F_{y} =\frac{1}{2}\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\sin^{2}\alpha \cos \alpha S_{\alpha }\); (3.5)
\( F_{x} =\frac{1}{2}\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\sin^{3}\alpha S_{\alpha }\); (3.6)
Коэффициенты подъемной силы и лобового сопротивления соответственно из (3.5) и (3.6) имеют вид:
\( C_{y} = (1 -\frac{\upsilon }{a})\sin^{2}\alpha \cos \alpha\); (3.7)
\( C_{x} = (1 -\frac{\upsilon }{a})\sin^{3}\alpha\); (3.8)
4. ФРОНТ УДАРНОЙ ВОЛНЫ (ФУВ) КАК ГРАНИЦА ПОГРАНИЧНОГО СЛОЯ
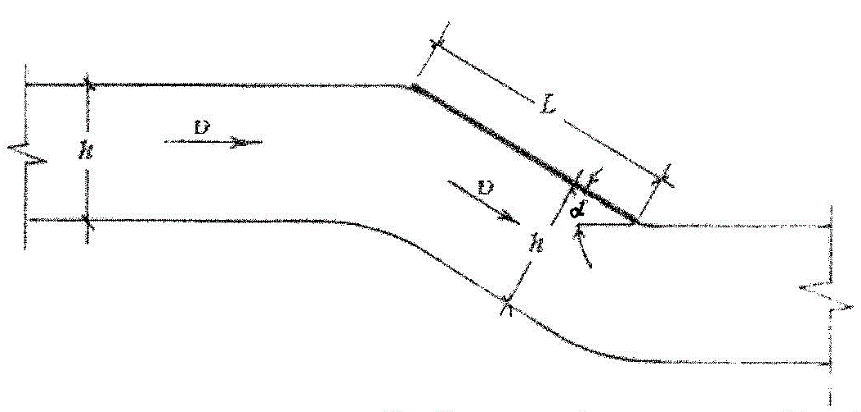
Рис. 3. Схема обтекания пластинки с углом атаки $\alpha$
При набегании струи потока жидкости толщиной $h$ и неограниченной ширины, плоской струи, на пластинку с углом атаки $\alpha$, каждая частица струи жидкости, набегающей на пластинку, испытывает со стороны пластинки действие внешнего подпора
$J = tg\alpha$; (4.1)
отклоняющего частицы струи от прямолинейного движения и увлекающего их в движение вдоль пластинки.
Каждой струе жидкости с ее толщиной $h$ и скоростью движения $\upsilon$ соответствует свой внутренний гидравлический уклон, который можно определить, располагая физической формулой скорости равномерного движения жидкости [2, §7] (7.28), имеющей вид:
\( \upsilon =\frac{6}{\alpha }\sqrt{20g\frac{R}{\alpha }J}\); (4.2)
Для плоского потока при бесконечной его ширине, глубина потока становится его гидравлическим радиусом $R = h$, а корректив кинетической энергии $\alpha$, для высокоскоростных потоков аэродинамики стремится к единице, $\alpha \approx 1.0$.
Окончательно приведенная выше физическая формула (4.2) скорости гидравлики, для плоского потока аэродинамики принимает вид
\( \upsilon = 6\sqrt{20ghJ}\); (4.3)
Из (4.3) внутренний гидравлический уклон струи воздуха определяется в виде
\( J =\frac{\upsilon^{2}}{720gh}\); (4.4)
где $\upsilon$ – скорость струи;
$h$ – глубина плоского потока струи;
$g$ – ускорение свободного падения тел.
Определив по (4.4) для заданной струи со скоростью $\upsilon$ и глубиной $h$ ее внутренний гидравлический уклон $J$ и сравнивая его с внешним гидравлическим подпором от пластинки $J$ по (4.1), действующим на струю, будем иметь два случая:
Случай 1. $J\le J_0$ – внутренний гидравлический уклон струи и внешний подпор от пластинки меньше или равны между собой. В этом случае струя потока жидкости, не изменяя своих параметров, будет проходить вдоль поверхности пластинки в виде плоского потока глубиной $h$ и скоростью движения $\upsilon$ (рис.3). При этом коэффициенты $C_y$ и $C_x$ следуют (3.7) и (3.8).
Скорость движения судна, воздушного или водного, возрастает от нуля до крейсерской скорости, воздействием энергетической установки на разгонном участке пути движения. Поэтому на всем этом пути скорость обтекания пластинки возрастает от нуля до соответствующей уклону $J$ и глубине $h$.
Случай 2. $J>J_0$ – уклон внутренний больше подпора внешнего от пластинки. В этом случае струя потока жидкости будет проходить вдоль поверхности пластинки, которая увеличивает свой угол атаки $\alpha$ до угла атаки $\phi_0$, гидравлический подпор от пластинки на струю становится гидравлическим уклоном, $J_0=tg\phi_0$, струи потока жидкости (рис.4).

Рис. 4. К объяснению возникновения фронта ударной волны
Увеличение угла атаки пластинки от $\alpha$ до $\phi_0$ объясняется следующим явлением.
Если в первом случае пограничный, пристенный, слой, вдоль которого осуществляется процесс обмена количеством движения набегающей струи с неподвижной пластинкой, расположен на пренебрежимо малом расстоянии от поверхности пластинки и параллелен ей, то во втором случае этот слой отходит от поверхности пластинки и устанавливается под углом $\phi_0$ к вектору скорости. Жидкость между границей пограничного слоя и пластинкой становится принадлежащей самой пластинке. С отступлением пограничного слоя на угол $\phi_0$ плоская пластинка превращается в виртуальное призматическое тело abc, у которого аэродинамические характеристики, подъемная сила и сила лобового сопротивления определяются гранью ab, с углом атаки $\phi_0$, а не $\alpha$.
Приложенное по нормали к площади пластинки $S$ с углом атаки $\phi_0$ давление определяет силу нормального давления на пластинку набегающей струи
\( F_{N_{\alpha }} =\frac{1}{2}\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\sin^{2}\phi_{0}S_{\alpha }\); (4.5)
Проекция этой силы на вертикальную ось дает подъемную силу пластинки с углом атаки $\phi_0$
\( F_{y} =\frac{1}{2}\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\sin^{2}\phi_{0}\cos \alpha S_{\alpha }\); (4.6)
и силу лобового сопротивления
\( F_{x} =\frac{1}{2}\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\sin^{3}\phi_{0}S_{\alpha }\); (4.7)
Коэффициенты подъемной силы и лобового сопротивления в этом случае отличаются от первого случая и имеют вид:
\( C_{y} = (1 -\frac{\upsilon }{a})\sin^{2}\phi_{0}\cos \alpha\); (4.8)
\( C_{x} = (1 -\frac{\upsilon }{a})\sin^{3}\phi_{0}\); (4.9)
где $\phi_0$ – угол атаки пограничного слоя; угол ФУВ.
Отступивший от поверхности пластинки на угол $\phi_0$ пограничный слой, его поверхность, является ни чем иным, как известным в аэромеханике ФУВ, наблюдаемым при околозвуковых скоростных движениях в воздушной среде.
В действительности ФУВ, являясь поверхностью пограничного слоя, по которой развивается процесс обмена количеством движения, идущий по схеме гидравлического удара, всегда присущ телам, движущимся в воздушной среде. Но в тех случаях, когда тангенс внешнего угла атаки тела больше или равен внутреннему, собственному гидравлическому уклону набегающего потока, то ФУВ, или граница пограничного слоя, прижат к поверхности тела.
Если же набегающий поток жидкости имеет значительно больший собственный гидравлический уклон и соответствующую ему высокую скорость движения, то, в соответствии с третьим законом Ньютона, когда действие равно противодействию, у тела, воспринимающего набегающий поток, под поверхность его пограничного слоя нагнетается жидкость; в результате пограничный слой, или ФУВ, устанавливается под углом $\phi_0$, тангенс которого равен гидравлическому уклону набегающего потока. Таким образом, устанавливается равновесие между силой давления набегающего потока и реакцией тела, воспринимающего действие набегающего потока.
Следуя вышеизложенному, возможно определить (рис.3) критическую скорость движения пластинки длиной $L$ и углом атаки $\alpha$, при которой пограничный слой, или ФУВ, начнет отходить от поверхности пластинки, тем самым увеличивая её аэродинамические характеристики.
\( \upsilon_{кр} = 6\sqrt{20ghtg\alpha }\); (4.10)
в формуле (4.10):
\( h = L\sin \alpha\); (4.11)
$h$ – толщина струи потока, набегающей на неподвижную пластинку, или толщина покоящейся жидкости, на которую набегает пластинка со скоростью $\upsilon_{кр}$.
К примеру, определить критическую скорость движения пластинки длиной $L=8.0м$ и углом атаки $\alpha = 10^{\circ}$, выше которой пограничный слой начнет отклоняться от поверхности пластинки при ее движении в воздушной среде с коэффициентом кинематической вязкости $\nu=1.43\cdot10^{-5}м/с^2$.
По формуле (4.10), определяем критическую скорость
\( \upsilon_{кр} = 6\sqrt{20⋅9.81⋅8\sin 10^{\circ} tg10^{\circ} } = 41.50 м/с\).
Для этой же пластинки определим, на какой угол отклонится пограничный слой, или ФУВ, при движении ее у поверхности земли в воздушной среде со скоростью 280 м/с. Из формулы (4.10)
\( \phi_{0} = arctg\left(\frac{\upsilon^{2}}{720gL\sin \alpha }\right)\); (4.12)
\( \phi_{0} = arctg\left(\frac{280^{2}}{720⋅9.81⋅8\sin 10^{\circ} }\right) = 82.7^{\circ}\).
Не приводя вычислений, приведем положение ФУВ, соответствующее дальнейшему повышению скорости движения пластинки:
$\upsilon=290 м/с;$ $\upsilon=295 м/с;$ $\upsilon=300 м/с;$ | $\phi_0=83.35°;$ $\phi_0=83.56°;$ $\phi_0=83.78°;$ |
То есть, при достижении пластинкой с углом атаки $\alpha = 90^{\circ}$ скорости движения, 300 м/с, приближающейся к скорости звука у земли, 340 м/с, ФУВ устанавливается практически под углом 90° к вектору скорости, что хорошо согласуется с данными экспериментальной, практической аэромеханики.
Определим коэффициент подъемной силы $C_y$ для пластинки длиной $L=2.5м$ с углом атаки $\alpha = 15^{\circ}$, движущейся в воздушной среде со скоростью $\upsilon=0.7M$, где $M=\frac{\upsilon}{a}$ – число Маха, т.е. $\upsilon=210м/с$.
Угол атаки струи $\phi_0$, он же является углом атаки фронта ударной волны, определился равным
\( \phi_{0} = arctg\left(\frac{\upsilon^{2}}{720gL\sin \alpha }\right) = arctg\left(\frac{210^{2}}{720⋅9.81⋅2.5⋅0.259}\right) = 84^{\circ}\).
Гидравлический уклон высокоскоростной струи равен
\( J_{0} = tg\phi_{0} = 9.65\);
Сравнивая гидравлические уклоны, имеем второй случай обтекания, когда $J_0=9.65>J=0.268$.
Коэффициент подъемной силы определяем по (4.8)
$C_{y} =\left(1 -\frac{\upsilon }{a}\right)\sin^{2}\phi_{0}\cos \alpha = \\ (1 -\frac{210}{300})\sin^{2}84^{\circ} \cos 15^{\circ} = 0.28$.
Не приводя вычислений, для данной пластинки с постоянным углом атаки $\phi=15°$, на рисунке 5, приведен график изменения коэффициента подъемной силы в зависимости от скорости $\upsilon$, изменяющейся до скорости звука. Расчет графика выполнен по формулам (3.7) и (4.8).
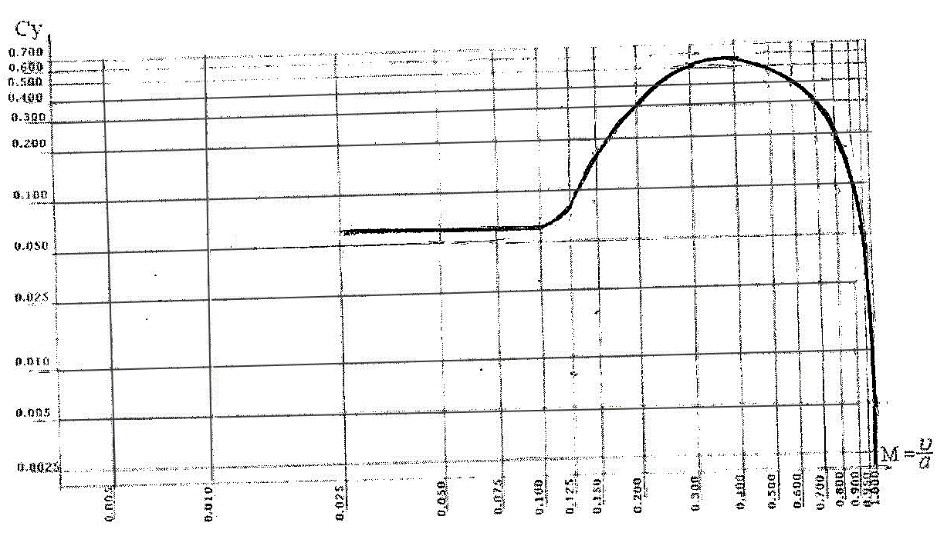
Рис. 5. Изменение коэффициента подъемной силы пластинки в воздушной среде длиной 2.5 м и углом атаки $\alpha = 15^{\circ}$
Из графика видно, что при скорости движения пластинки от 7.5 м/с до 30 м/с коэффициент подъемной силы имеет малое значение в пределах 0.06. На этом участке движения у самолетов, для увеличения подъемной силы и сокращения длины разбега, в работу включаются закрылки крыла. Далее от скорости пластинки 30 м/с идет интенсивное нарастание коэффициента подъемной силы.
С этого момента от поверхности пластинки начинает отделяться пограничный слой, фронт ударной волны, увеличивая угол атаки $\phi_0$. При максимальном коэффициенте подъемной силы угол атаки фронта ударной волны составляет $\phi=72.4°$ при скорости пластинки 120 м/с.
После скорости $\upsilon=0.4M$, при дальнейшем увеличении скорости, начинается интенсивное падение коэффициента подъемной силы. При достижении пластинкой скорости, равной скорости звука, подъемная сила пластинки обращается в нуль.
График $C_y=f(\upsilon)$ хорошо согласуется с данными экспериментальной аэромеханики: «Обычные характеристики крыла ($C_y;C_x$ и др.), как показывают эксперименты, сильно изменяются в зависимости от скорости» [3, с.105], «Коэффициент подъемной силы $C_y$ сначала возрастает…, а затем начинает падать вначале медленно, а потом резко» [3, c.109].
II. АЭРОДИНАМИКА ВОЗДУШНОГО СУДНА
5. ВОЗДУШНОЕ СУДНО И ЭКВИВАЛЕНТНОЕ ЕМУ СУДНО
Как доказано в [1], каждому реальному судну водного или воздушного транспорта существует виртуальное судно такой же массы M и постоянной по длине площади поперечного сечения $\omega$, равной площади миделевого сечения реального судна по фюзеляжу.
Длина такого виртуального судна $l_{ц}$ показана на рис. 6.
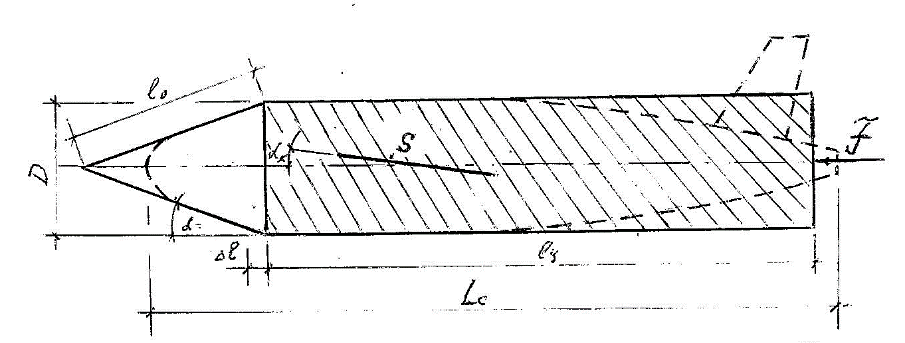
Рис. 6. Схема воздушного судна и виртуального цилиндрического судна
Обозначения на рис. 6:
$\Delta l$ – деформация упругого сжатия корпуса движущей силой F, на которую отклоняется носовая часть при ее периодических ударах по встречной жидкости, воздуху;
$D$ – диаметр фюзеляжа;
$L_{с}$ – длина реального судна;
$l_{ц}$ – длина цилиндрического виртуального судна, принимается равной
$l_{ц}$=0.85$L_{с}$; (5.1)
$l_{о}$ – длина образующей конуса входной части;
$\alpha$ – угол атаки судна, из практики, у ВС пассажирского флота лежит в пределах $\alpha = 20^{\circ}$;
$\alpha_{к}$ – угол атаки крыла; принимается у реальных судов 7-8 градусов;
$S$ – площадь крыла;
$F$ – движущая сила, определяется тягой Tx двигателей по паспорту;
\( F = gT_{x}\); (5.2)
где $g = 9.81м/с^{2}$ – ускорение свободного падения.
Масса виртуального судна определена величиной взлетной массы M реального воздушного судна и включает в себя массу всех выступающих частей корпуса, носовой части, крыльев и т.п.
6. РАСЧЕТНЫЕ ФОРМУЛЫ АЭРОДИНАМИКИ
Законы движения в жидкостях, под которыми понимаются вода и воздух, едины, поэтому формулы гидродинамики, вывод и обоснование которых приведены в [1], действительны и для аэродинамики.
Поэтому формулы аэродинамики даются в окончательном виде, без вывода, для практического пользования ими при проектировании и научных исследованиях.
6.1. КРЕЙСЕРСКАЯ СКОРОСТЬ
\( \upsilon =\sqrt{\frac{N}{M}n_{0}T}\); (6.1)
$N$ – мощность двигателей, кВт.
Определяется произведением паспортных значений движущей силы F (тяги Tx) на крейсерскую скорость υ:
\( N = F\upsilon\); (6.2)
$M$ – взлетная масса, т;
\( n_{0}\) – разгонное число;
$T$ – время оседлости, с.
6.2. РАЗГОННОЕ ЧИСЛО
У движителей, использующих в качестве упора не Землю, а реакцию отбрасываемой жидкости [1], характер действия движущей силы является не непрерывно-статическим, а дискретно-ударным, когда судно разгоняется до крейсерской скорости отдельными приращениями скорости Δυ
\( \Delta \upsilon = GT\); (6.3)
$G$ – ускорение судна, м/с2;
\( G =\frac{F}{M}\); (6.4)
Равномерное движение судна с крейсерской скоростью полета наступает тогда, когда судно воспримет от силовой установки $n_{0}$ импульсов движущей силы, а крейсерская скорость примет значение, соответствующее выражению (3.6) в [1]
\( \upsilon = n_{0}\Delta \upsilon\); (6.5)
Разгонное число $n_{0}$, это количество импульсов движущей силы на участке ускоренного движения судна, результатом действия которых судно разгоняется из состояния покоя до равномерного движения с крейсерской скоростью полета, определяется формулой (5.3) в [1].
\( n_{0} =\frac{1}{\sin^{1.5}\alpha }\frac{R}{2}\sqrt{\frac{a}{\nu l_{ц}}}\); (6.6)
$\alpha$ – угол атаки судна;
$R$ – гидравлический радиус корпуса при его диаметре $D$;
\( R =\frac{D}{4}\); (6.7)
\( a = 300м/с\) – скорость звука в воздухе на высоте 10 тыс. м над уровнем моря;
\( \nu = 1.43⋅10^{ - 5}\frac{м^{2}}{с}\) – коэффициент кинематической вязкости воздуха;
$l_{ц}$ – длина виртуального судна по (5.1).
6.3. ВРЕМЯ ОСЕДЛОСТИ
Время T оседлости судна в (6.1) – это время, в течение которого, по закону инерции Ньютона, судно сохраняет состояние покоя и не начинает движение с момента приложения к нему движущей силы, определяется формулой (3.1) в [1]
\( T =\frac{l_{ц}}{c}\); (6.8)
$c$ – скорость звука по корпусу судна, скорость распространения по нему деформации упругого сжатия, ударной волны.
Корпус воздушных судов включает в себя набор разных материалов (сплавы различных металлов, стекло, оргстекло, уплотнители и т.п.), что не позволяет принимать скорость звука по корпусу через модуль Юнга, подобно корпусу судов водного транспорта из стали со скоростью звука 5100 м/с.
Для жидкостей получена связь силы движущей $F$ и силы сопротивления трения $F_{тр}$ через отношение скорости звука по жидкости к скорости звука по корпусу в виде формулы (7.4) в [1]
\( F_{тр} =\frac{a}{2c}F\); (6.9)
Из (6.9) определяется скорость звука по корпусу воздушного судна формулой
\( c = a\frac{F}{2F_{тр}}\); (6.10)
6.4. СИЛА СОПРОТИВЛЕНИЯ ТРЕНИЯ
Сила трения по боковой поверхности корпуса судна определяется из равенства (7.4) в [1], снабженного коэффициентом \(\frac{\rho_{0}}{\rho}\), где $\rho_{0}$ – взлетная плотность массы М по объему судна, кг/м3; определяется по формуле
\( \rho_{0} =\frac{M}{\omega l_{ц}}\); (6.11)
\( \rho = 1.23кг/м^{3}\) – плотность воздуха.
Кроме того, в указанном равенстве раскрывается коэффициент турбулентной вязкости $\mu_{T}$ формулой (4.4) в [1] в виде
\( \mu_{T} = n_{0}\mu\); (6.12)
\( \mu = 1.76⋅10^{ - 5}\frac{кг}{мс}\) – коэффициент динамической вязкости воздуха.
Вязкость жидкости, омывающей корпус судна [1, §4], растет вместе с ростом скорости судна, достигая максимального значения пропорционально разгонному числу $n_{0}$.
Окончательно формула силы сопротивления трения при движении судна в воздушной среде приняла вид
\( F_{тр} = \sin^{3}\alpha \mu n_{0}\frac{2\upsilon }{R}\chi l_{ц}\frac{\rho_{0}}{\rho }\); (6.13)
\( \chi\) – периметр корпуса;
\( \chi = \pi D\); (6.14)
6.5. СИЛА ЛОБОВОГО СОПРОТИВЛЕНИЯ
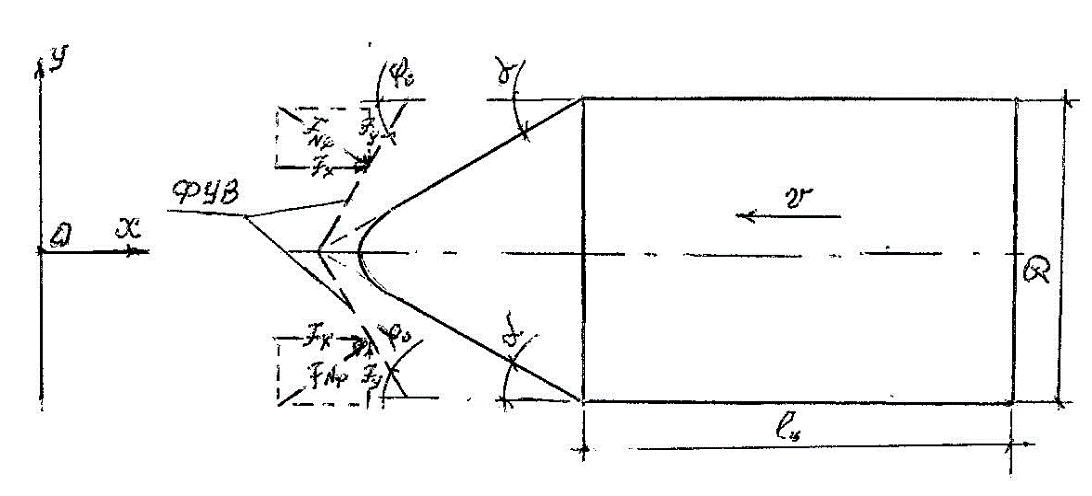
Рис. 7. Схема сил лобового сопротивления
Обозначения на рис. 7:
$F_{N_{\phi }}$ – сила нормального давления на боковую поверхность конуса ФУВ;
$F_{x},F_{y}$ – проекции силы \( F_{N_{\phi }}\) на горизонтальную и вертикальную оси декартовых координат;
$D$ – диаметр фюзеляжа;
ФУВ – фронт ударной волны.
Набегая на воздушную среду (рис.7), согласно схемы действующих сил, сила сопротивления в проекции на ось y, $F_{y}$, равна нулю, так как является силой всестороннего сжатия корпуса по отношению оси x при симметричном обтекании корпуса.
Сила в проекции на ось x, $F_{x}$, является силой лобового сопротивления движению судна с углом $\phi_0$ атаки ФУВ. Согласно §4 отклонение угла атаки судна от гидравлического уклона \( J = tg\alpha\) до гидравлического уклона $J_{0} = tg\phi_{0}$ происходит из-за превышения скорости судна над критической скоростью $\upsilon_{кр}$, при которой начинается отклонение пограничного слоя от его плотного прилегания к поверхности носовой части судна.
Крейсерская скорость судна, при которой происходит максимальное отклонение пограничного слоя, определяется формулой (4.10), в которой заменяется глубина $h = L\sin \alpha$ плоского потока гидравлическим радиусом $R$ потока вдоль цилиндрической поверхности диаметра $D$. Кроме того, за счет сжимаемости воздуха, гидравлический радиус уменьшается коэффициентом, в виде отношения скорости υ судна к скорости a звука в воздушной среде, то есть
\( R_{0} = R\frac{\upsilon }{a}\); (6.15)
Из преобразованной формулы (4.12) угол атаки ФУВ судна определяется формулой
\( \phi_{0} = arctg\left(\frac{\upsilon^{2}}{720gR\frac{\upsilon }{a}}\right)\); (6.16)
После сокращений в (6.16) формула угла атаки ФУВ судна окончательно приводится к виду
\( \phi_{0} = arctg\left(\frac{\upsilon a}{720gR}\right)\); (6.17)
Площадь поверхности носового конуса воздушного судна, при его образующей $l_{о}$ на рис.6, как следует из математики, определяется формулой
\( S_{\alpha } = \pi rl_{0}\); (6.18)
где где $r =\frac{D}{2}$ – радиус фюзеляжа;
$l_{о}$ – образующая конуса носовой части;
\( l_{0} =\frac{r}{\sin \alpha }\); (6.19)
Подставляя (6.19) в (6.18), получаем площадь поверхности носовой части в виде формулы
\( S_{\alpha } =\frac{\pi r^{2}}{\sin \alpha }\); (6.20)
Из (6.20) следует, что угол атаки судна выражается формулой в виде
\( \alpha = \arcsin\frac{\omega }{S_{\alpha }}\); (6.21)
где $\omega$ – площадь поперечного сечения фюзеляжа;
\( S_{\alpha }\) – площадь боковой поверхности носового конуса судна.
Особенностью движения в воздушной среде является то, что при образовании перед судном ФУВ с углом атаки $\phi_0$, силу лобового сопротивления определяет площадь носовой поверхности корпуса воздушного судна \( S_{\alpha }\), определяемой формулой
\( S_{\alpha } =\frac{\omega }{\sin \alpha }\); (6.22)
Поэтому сила лобового сопротивления, следуя (4.7), представляется формулой в виде
\( F_{лоб} =\frac{1}{2}\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\sin^{3}\phi_{0}S_{\alpha }\); (6.23)
Эта сила, вместе с силой трения по боковой поверхности судна (6.13), определяет движущую силу воздушного судна
\( F = F_{лоб} + F_{тр}\); (6.24)
6.6. ПОДЪЕМНАЯ СИЛА КРЫЛА
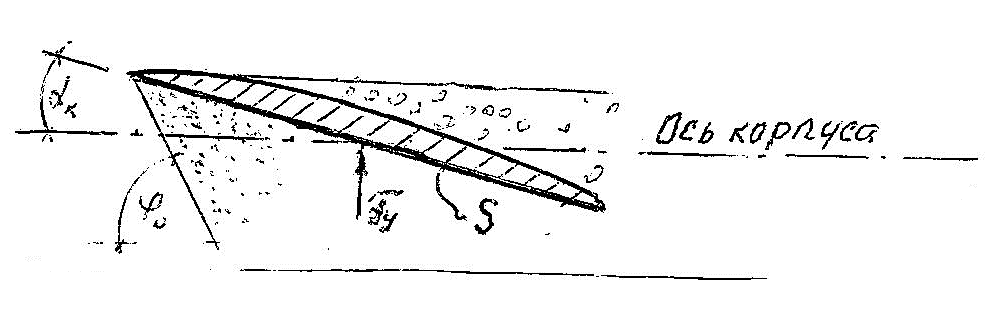
Рис. 8. Схема обтекания крыла самолета
Обозначения на рис.8:
$\alpha_{к}$ – угол атаки крыла; из практики авиастроения равен 7-8 градусам;
$\phi_0$ – угол атаки ФУВ судна, из-за равенства расхода воздушного потока на лобовую поверхность судна и на поверхность крыла, определяется формулой (6.17);
$S$ – площадь крыла, м2.
Подъемная сила крыла следует формуле (4.6), как проекция на вертикальную ось силы нормального давления струи воздуха на площадь $S$ пластинки с углом атаки $\alpha_{к}$ в виде
\( F_{y} =\frac{1}{2}\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\sin^{2}\phi_{0}\cos \alpha_{к}S\); (6.25)
Заменяя в (6.25) левую часть равенства весом воздушного судна
\( P = Mg\); (6.26)
получаем формулу необходимой площади крыла самолета в виде
\( S =\frac{2Mg}{\rho \upsilon^{2}(1 -\frac{\upsilon }{a})\sin^{2}\phi_{0}\cos \alpha_{к}}\); (6.27)
7. ПРОВЕРКА ФОРМУЛ НА РЕАЛЬНЫХ ВОЗДУШНЫХ СУДАХ
Проверка истинности формулы (6.1) крейсерской скорости осуществлялась по паспортным характеристикам самолетов со взлетной массой от 161.6 т (Ил-62) до 560 т (Аэробус А380).
При паспортной тяге двигателей, по предложенным формулам определялась расчетом крейсерская скорость воздушного судна, которая сравнивалась с действительной крейсерской скоростью, зафиксированной в ходе натурных летных испытаний воздушных судов.
Расчеты выполнялись в следующей последовательности.
7.1. ПОРЯДОК РАСЧЕТА И ФАКТИЧЕСКИЙ УГОЛ АТАКИ α0
С достаточной достоверностью истинности предлагаемых аэродинамических представлений и вполне допустимой погрешностью расчетных характеристик с натурными, за основу принято следующее утверждение.
При движении тел в жидкостях, водной или воздушной среде, подчиняющемся единому гидромеханическому закону, соотношение силы сопротивления трения с силой движущей, выявленное для судов водного транспорта, (7.4) в [1], распространяется и на движение в воздушной среде. Это соотношение имеет вид
\( Э =\frac{F_{тр}}{F} =\frac{a}{2c}\); (7.1)
где \( a = 300м/с\) – скорость звука в воздушной среде;
$c$ – скорость звука по корпусу воздушного судна.
7.2. ЭНЕРГЕТИЧЕСКИ НАИВЫГОДНЕЙШЕЕ СООТНОШЕНИЕ СИЛ
При движении в водной среде соотношение (7.1), при скорости звука в воде, \( a = 1435м/с\), и скорости звука по стальному корпусу, \( c = 5100м/с\), численно равно
\( Э =\frac{a}{2c}\approx 0.14\); (7.2)
Это соотношение показывает, что при переходе в равномерное движение судов водного транспорта доля сопротивления в движущей силе, приходящаяся на силу трения составляет 14 процентов.
\( F_{тр} = 0.14F\); (7.3)
Остальная доля сопротивления в движущей силе, 86 процентов, приходится на лобовое сопротивление:
\( F_{лоб} = 0.86F\); (7.4)
Сохраняя численное значение соотношения (7.2) действующим и при движении в воздушной среде, определяем из него скорость звука по корпусу воздушного судна при переходе его движения из ускоренного в равномерный режим
\( c =\frac{a}{2Э}\); (7.5)
На практике возможны три случая движения в воздушной среде в зависимости от численного значения соотношения (7.1)
$\begin{array}{c} \ а)Э<0.14 \\ \ б)Э>0.14 \\ \ в)Э = 0.14 \\ \end{array}$ (7.6)
В случае (7.6 а), воздушное судно перегружено от оптимальной взлетной массы, когда модуль упругости судна возрастает за счет роста взлетной плотности массы по его объему
\( E_{c} = \rho_{0}c^{2}\); (7.7)
При этом в движущей силе преобладает сила лобового сопротивления из-за роста модуля упругости корпуса.
В случае (7.6 б), воздушное судно оказывается недогруженным до оптимальной взлетной массы, когда в движущей силе преобладает сила трения, а не сила лобового сопротивления.
В случае (7.6 в) наблюдается энергетически наивыгоднейшее соотношение сил, когда сопротивление движению воздушного судна определено сопротивлением только самой воздушной среды, ее упругостью, а не увеличившейся взлетной массой судна ради повышения его рентабельности за счет увеличения пассажировместимости.
Определившаяся по (7.5) скорость звука по корпусу воздушного судна позволяет определять время оседлости судна
\( T =\frac{l_{ц}}{c}\); (7.8)
Принимая угол атаки виртуального цилиндрического судна равным \( \alpha_{ц} = 90^{\circ}\), по формуле (6.6) определяем для такого судна, с торцевой передней гранью без носовых обводов, разгонное число при \( \sin \alpha_{ц} = 1.0\) по формуле
\( n_{ц} =\frac{R}{2}\sqrt{\frac{a}{\nu l_{ц}}}\); (7.9)
Возможная скорость цилиндрического судна без носовых обводов, массой M и движущей силой F, определяется формулой
\( \upsilon_{ц} = n_{ц}GT\); (7.10)
где $G$ – ускорение судна, м/с2;
\( G =\frac{F}{M}\); (7.11)
Фактическое разгонное число исследуемого судна при паспортной его крейсерской скорости $\upsilon$ определяется формулой
\( n_{0} =\frac{\upsilon }{\upsilon_{ц}}n_{ц}\); (7.12)
Отношение фактической крейсерской скорости к скорости цилиндрического судна в (7.12) является значением коэффициента в формуле разгонного числа, увеличивающего его значение за счет носовых обводов с углом атаки $\alpha_{0}$, то есть
\(\frac{1}{\sin^{1.5}\alpha_{0}} =\frac{\upsilon }{\upsilon_{ц}}\); (7.13)
Решая (7.13), определяется фактический угол атаки воздушного судна по формуле
\( \alpha_{0} = \arcsin (\frac{\upsilon_{ц}}{\upsilon })^{\frac{2}{3}}\); (7.14)
Расчеты по проверке предлагаемых формул аэродинамики сведены в таблицу 1.
Таблица 1
Расчет крейсерской скорости действующих авиалайнеров
Показатели, номер формулы | Значения | |||||||
Ил-96-300 | Базовый Ил-86 | Ил-62 | Аэробус А380 | |||||
I Характеристики паспортные | ||||||||
| 1. Масса взлетная; | $M,т$ | 250 | 208 | 161.6 | 560 | |||
| 2. Крейсерская скорость; | $\upsilon,м/с $ км/ч | 241.67/ 870 | 241.67/ 870 | 236.1/ 850 | 250/ 900 | |||
| 3. Диаметр фюзеляжа; | $D,м$ | 6.08 | 5.70 | 3.75 | 7.14 | |||
| 4. Площадь крыла; | $S,м^{2}$ | 350 | 320 | 279.55 | 845 | |||
| 5. Тяга двигателей; | $T_{x},тc$ | 64 | 52 | 42 | 138.6 | |||
| 6. Длина судна; | $L_{c},м$ | 55.345 | 59.50 | 53.12 | 73.0 | |||
II Исходные данные | ||||||||
| 7. Масса взлетная; | $M,т$ | 250 | 208 | 161.6 | 560 | |||
| 8. Сила движущая; | (5.2) | $F,кН$ | 627.84 | 510.12 | 412.02 | 1360 | ||
| 9. Мощность двигателей; | (6.2) | $N,кВт$ | 1.52·105 | 1.23·105 | 9.73·104 | 3.4·105 | ||
| 10. Крейсерская скорость; | п.2 | $\upsilon, м/с$ | 241.67 | 241.67 | 236.1 | 250 | ||
| 11. Угол атаки судна; | $\alpha$, град | 20 | 20 | 20 | 20 | |||
| 12. Площадь сечения фюзеляжа; | $\omega$,м2 | 29.03 | 25.52 | 11.04 | 40.04 | |||
| 13. Площадь носового конуса; | (6.20) | $S,м^{2}$ | 84.88 | 74.62 | 32.3 | 117.07 | ||
| 14. Периметр фюзеляжа; | $\pi D$ | $\tau ,м$ | 19.10 | 17.90 | 11.78 | 22.43 | ||
| 15. Гидравлический радиус; | (6.7) | $R,м$ | 1.52 | 1.425 | 0.9375 | 1.785 | ||
| 16. Длина виртуального судна; | (5.1) | $l_{ц},м$ | 47.04 | 50.58 | 45.15 | 62.05 | ||
| 17. Взлетная плотность; | (6.11) | $\rho_{0},кг/м^{3}$ | 183.07 | 161.14 | 324.2 | 225.4 | ||
| 18. Угол атаки ФУВ; | (6.17) | $\phi_{0}$, град | 81.6 | 82.10 | 84.61 | 80.46 | ||
| 19. Угол атаки крыла; | $\alpha_{к}$, град | 7.0 | 7.0 | 7.0 | 7.0 | |||
III Характеристики расчетные | ||||||||
| 20. Соотношение сил $\frac{F_{тр}}{F}$ | \( Э =\frac{a}{2c}\); | 0.14 | 0.16 | 0.10 | 0.04 | |||
| 21. Скорость звука по корпусу; | (7.5) | c, м/с | 1071.43 | 937.5 | 1500 | 3750 | ||
| 22. Время оседлости; | (6.8) | $T$, с | 0.0439 | 0.054 | 0.03 | 0.0165 | ||
| 23. Разгонное число вирт.судна; | (7.9) | $n_{ц}$ | 508 | 459 | 319 | 519 | ||
| 24. Скорость виртуального судна; | (7.10) | $\upsilon_{ц}$, м/с | 56 | 60.79 | 24.40 | 20.39 | ||
| 25. Фактическое разгонное число; | (7.12) | $n_{0}$ | 2192 | 1825 | 3087 | 6239 | ||
| 26. Фактический угол атаки; | (7.14) | $\alpha_{0}$ | 22.15 | 23.47 | 12.7 | 10.97 | ||
| 27. Крейсерская скорость; | (6.1) | $\upsilon$, м/с | 241.88 | 241.4 | 236.02 | 250 | ||
| 28. Погрешность; $\frac{п.27 - п.2}{п.2}⋅100$ | $\Delta \upsilon ,\%$ | +0.09 | -0.11 | -0.03 | 0.00 | |||
| 29. Сила трения; | (6.13) | $F_{тр}$, кН | 87.90 | 81.44 | 40.76 | 54.13 | ||
| 30. Фактическая площадь носовой части; | (6.22) | $S_{\alpha_{0}}, м^{2}$ | 77.00 | 64.08 | 50.22 | 210.41 | ||
| 31. Лобовое сопротивление; | (6.23) | $F_{лоб}, кН$ | 520.47 | 434.93 | 364.52 | 1297.49 | ||
| 32. Сила движущая; | (6.24) | $F$, кН | 608.37 | 516.44 | 405.28 | 1351.62 | ||
| 33. Погрешность;$\frac{п.32 - п.8}{п.8}⋅100$ | $\Delta F,\%$ | -3.1 | +1.24 | -1.64 | -0.62 | |||
| 34. Площадь крыла; | (6.27) | $S,м^{2}$ | 353.9 | 300.0 | 220.63 | 885.7 | ||
| 35. Погрешность; $\frac{п.34 - п.4}{п.4}⋅100$ | $\Delta S,\%$ | +1.11 | -6.25 | -21.0 | +4.8 | |||
| 36. Фактическое соотношение; | $Э =\frac{F_{тр}}{F}$ | 0.145 | 0.158 | 0.10 | 0.04 | |||
| 37. Погрешность; $\frac{п.36 - п.20}{п.20}⋅100$ | $\Delta Э,\%$ | 3.57 | -1.25 | 0.00 | 0.00 | |||
| 38. Скорость звука по корпусу; | (6.10) | c, м/с | 1038.2 | 950.85 | 1491.5 | 3745.5 | ||
| 39. Погрешность; $\frac{п.38 - п.21}{п.21}⋅100$ | $\Delta c,\%$ | -3.1 | +1.42 | -0.56 | -0.12 | |||
Пренебрежимо малая погрешность расчетных характеристик судов над фактическими, п.28; 33; 37; 39, когда отклонения от фактических значений не превышают пяти процентов, подтверждают соответствие предлагаемых аэродинамических представлений на движение в воздушной среде, истинным, фактическим характеристикам этого движения.
Завышение фактического угла атаки $\alpha_{0}$ у Ил-96 и Ил-86 от геометрического угла $\alpha = 20^{\circ}$, соответственно до $\alpha_{0} = 22.15^{\circ}$ и $\alpha_{0} = 23.47^{\circ}$, п.26, объясняется наличием на носовой поверхности смотровых окон кабины пилотов, служащих дополнительным местным гидравлическим сопротивлением.
Завышение на 21% фактической площади крыла у Ил-62, п.34, является волевым конструкторским запасом из-за возникших заметных поперечных вибраций корпуса при продувке лайнера в аэродинамической трубе на околозвуковом режиме из-за перегруза Ил-62 над оптимальной его взлетной массой.
Занижение фактического угла атаки, п.26, у Ил-62 и А380 до, соответственно, $\alpha_{0} = 12.7^{\circ}$ и $\alpha_{0} = 10.97^{\circ}$, вместо их геометрических углов атаки $\alpha = 20^{\circ}$, объясняется лишь превышением у этих судов взлетной массы над оптимальной взлетной массой.
III. СВЕРХЗВУКОВОЙ АВИАЛАЙНЕР
8. НЕЙТРАЛИЗАЦИЯ ЛОБОВОГО СОПРОТИВЛЕНИЯ
Природа лобового сопротивления при движении в жидкости раскрыта в [1, §8]. Сущность этого явления заключена в превышении энергопроводности, скорости звука по корпусу судна над энергопроводностью, скоростью звука по встречной жидкости. По существу, скорость звука – это скорость распространения по материальному телу энергии его упругого местного сжатия, заключенной в ударной волне, перемещающейся по телу от молекулы к молекуле с огромной скоростью.
Деформации упругого сжатия, генерируемые по корпусу движущей силой с частотой $\frac{1}{T}$, где $T$ – время оседлости судна, пробегают по корпусу со скоростью звука и в виде ударов передаются встречной жидкости. Из-за меньшей скорости звука в жидкости, эти деформации не успевают высвобождаться, расширяться и рассеивать содержащуюся в них энергию упругого сжатия.
В результате у носовой поверхности судна накапливается энергия упругого сжатия жидкости, проявляющаяся у судов водного транспорта в виде напора $\Delta h$ подпорной волны, а у воздушных судов – в виде слоя сжатого воздуха повышенной плотности, ударной волны. По существу, подпорная волна у судов водного транспорта и ударная волна у воздушных судов являются следствием не крейсерской скорости $\upsilon$ хода судов, а следствием ударного давления $\rho_{0}\upsilon c$, оказываемого судами по встречной жидкости, где $\rho_{0}$ – плотность судна, кг/м3; $c$ – скорость звука по нему, м/с.
8.1. УСЛОВИЕ НЕЙТРАЛИЗАЦИИ
Условием нейтрализации силы лобового сопротивления является [1, §8] уменьшение скорости распространения деформации упругого сжатия по корпусу, скорости звука по нему, до эффективной скорости $c_{эф}$ в два раза меньшей, чем скорость звука по встречной жидкости, воздушной среде, то есть
\( c_{эф} =\frac{a}{2}\); (8.1)
\( a = 300м/с\), скорость звука в воздушной среде.
Этим уменьшается упругость корпуса судна до эффективной упругости, присущей обитателям жидкой среды, дельфинам, обеспечивающей им движение в воде с отрицательным градиентом динамического давления, когда напряжения упругого сжатия во встречной жидкости у носовой поверхности тела рассеиваются, исчезают быстрее, чем возникают от набегания на нее тела дельфина [1, §8.1].
Из соотношения сил (7.1) следует, что при $c_{эф}$ по (8.1) соотношение превращается в единицу, при котором движущая сила F становится определена только силой вязкого трения $F_{тр}$, при отсутствии лобового сопротивления.
Уменьшением скорости звука по корпусу судна увеличивается время оседлости судна до эффективного времени оседлости в формуле крейсерской скорости в виде
\( T_{эф} =\frac{2l_{ц}}{a}\); (8.2)
Из таблицы 1, п.20, следует, что среди приведенных воздушных судов лишь Ил-96 создан и работает в зоне (7.6) энергетически наивыгоднейшего соотношения силы трения и движущей силы, при оптимальной взлетной плотности $\rho_{0} = 183.07кг/м^{3}$, когда сопротивление определено одной упругостью воздушной среды, а не перегруженностью судна.
Ил-86 так же находится практически в зоне энергетически наивыгоднейшего соотношения сил с небольшой недогруженностью до оптимальной взлетной массы при взлетной плотности $\rho_{0} = 161.14кг/м^{3}$.
Ил-62 и аэробус А380 перегружены, соответственно, в 1.77 и 1.23 раза и превращению в сверхзвуковые лайнеры не подлежат, так как из-за перегруженности, у них надо уменьшить взлетную массу, применить двигатели с меньшей тягой и уменьшить площадь крыла.
8.2. ЭФФЕКТИВНАЯ КРЕЙСЕРСКАЯ СКОРОСТЬ
При прочих равных параметрах, мощности двигателей, взлетной массе M и разгонном числе $n_{0}$, формула крейсерской скорости сверхзвукового лайнера отличается от формулы (6.1) крейсерской скорости дозвукового воздушного судна только величиной времени оседлости лайнера, увеличенного до $T_{эф}$ по (8.2) за счет уменьшения упругости корпуса судна и имеет вид
\( \upsilon_{эф} =\sqrt{\frac{N}{M}n_{0}T_{эф}}\); (8.3)
Степень увеличения крейсерской скорости сверхзвукового лайнера с его дозвуковой скоростью полета выражается формулой
\( \upsilon_{эф} = \upsilon\sqrt{\frac{T_{эф}}{T}}\); (8.4)
Подставляя в (8.4) $T_{эф}$ по (8.2) и T по (6.8), после сокращений на $l_{ц}$, формула эффективной крейсерской скорости полета сверхзвукового лайнера принимает конечный вид
\( \upsilon_{эф} = \upsilon\sqrt{\frac{2c}{a}}\); (8.5)
$c$ – скорость звука по корпусу воздушного судна;
\( a = 300м/с\) – скорость звука по воздуху на высоте полета 10 тыс. м над уровнем моря.
8.3. ПОДЪЕМНАЯ СИЛА И ПЛОЩАДЬ КРЫЛА
Переход на сверхзвуковой режим полета воздушного судна, при нейтрализованном лобовом сопротивлении из-за отсутствия образования перед судном слоя сжатого воздуха, ударной волны, сказывается на подъемной силе крыла из-за полета в разреженной атмосфере до плотности воздуха на высоте полета равной
\( \rho_{n} = 0.414кг/м^{3}\); (8.6)
Из [2, §2, (2.14)] известно, что при выведении из состояния покоя двухатомных молекул воздуха, азота N2 – 78% и кислорода O2 – 21%, полная энергия каждой молекулы должна быть увеличена в 4 раза над ее кинетической энергией поступательного движения.
Поэтому формула подъемной силы крыла сверхзвукового лайнера в общем виде следует формуле (3.5) и имеет вид
\( F_{y} = 2\rho_{n}\upsilon_{эф}^{2}\sin^{2}\alpha_{к}\cos \alpha_{к}S\); (8.7)
где $F_{y}$ – проекция на вертикальную ось силы нормального давления на пластинку с углом атаки α и площадью S;
\( 2\rho_{n}\upsilon_{эф}^{2}\) – учетверенная кинетическая энергия молекул воздуха, заключенная в единице объема, приобретаемая ими от набегания на них со скоростью $\upsilon_{эф}$ крыла лайнера;
\( \alpha_{к}\) – угол атаки крыла, принимается равным 8 градусам, на градус больше, чем в дозвуковом режиме полета;
$S$ – площадь крыла.
Заменяя в (8.7) левую часть равенства весом воздушного судна, формула необходимой площади крыла сверхзвукового воздушного судна принимает вид
\( S =\frac{Mg}{2\rho_{n}\upsilon_{эф}^{2}\sin^{2}\alpha_{к}\cos \alpha_{к}}\); (8.8)
8.4. СИЛА ТРЕНИЯ
При сверхзвуковом режиме полета и выполнении условия (8.1), обеспечивающем нейтрализацию лобового сопротивления, единственной силой сопротивления движущей силе $F$ является сила сопротивления $F_{тр}$ вязкого трения, формирующаяся на боковой поверхности корпуса судна, определяемая формулой
\( F_{тр} = \sin^{3}\alpha n_{0}\mu\frac{2\upsilon_{эф}}{R}\chi l_{ц}\frac{\rho_{0}}{\rho }\); (8.9)
Для Ил-96 скорость звука $c$ по корпусу судна, из таблицы 1, п.21, равна $c = 1071.43м/с$, а дозвуковая скорость полета составляет $\upsilon = 241.67м/с$, п.10 той же таблицы, следовательно, по формуле (8.5) сверхзвуковая крейсерская скорость полета Ил-96 определяется равной
\( \upsilon_{эф} = 241.67\sqrt{\frac{2⋅1071.43}{300}} = 645.89м/с(2325км/ч)\); (8.10)
Подставляя в (8.9) значение сверхзвуковой скорости Ил-96 по (8.10), а значения других параметров – из таблицы 1:
$\alpha_{0}$ – угол атаки, п.26;
$n_{0}$ – разгонное число, п.25;
$R$ – гидравлический радиус, п.15;
$l_{ц}$ – длина эквивалентного судна, п.16;
\( \chi\) – периметр корпуса, п.14;
\( \rho_{0}\) – взлетная плотность, п.17;
определяется величина силы сопротивления вязкого трения у Ил-96 при его сверхзвуковой скорости полета
$F_{тр} = \sin^{3}22.15^{\circ} ⋅2192⋅1.76⋅$
\( 10^{ - 5}\frac{2⋅645.89}{1.52}19.1⋅47.04\frac{183.07}{1.23} = 235.0кН\); (8.11)
Являясь единственной силой сопротивления движущей силе $F$, определяем значение движущей силы, как отношение мощности двигателей Ил-96, п.9 т.1, к скорости $\upsilon_{эф}$, то есть
\( F =\frac{N}{\upsilon_{эф}} =\frac{1.52⋅10^{5}}{645.89} = 235.33кН\); (8.12)
Сравнением (8.12) и (8.11) подтверждается, что движущая сила $F$ по (8.12), при сверхзвуковом режиме полета Ил-96, действительно уравновешивается силой трения $F_{тр}$ по (8.11).
Сверхзвуковой Ил-96 при крейсерской скорости полета (8.10) $\upsilon = 2325км/ч$, диаметре фюзеляжа – 6.08 м, пассажировместимости – 300 человек, тяге двигателей – 64 тс, по всем параметрам превзошел сверхзвуковой Ту-144с при его крейсерской скорости полета 2200 км/ч, диаметре фюзеляжа – 3.30 м, пассажировместимости – 120 человек и двигателях с тягой – 72 тс.
9. СПОСОБ И УСТРОЙСТВО НЕЙТРАЛИЗАЦИИ ЛОБОВОГО СОПРОТИВЛЕНИЯ
9.1. УМЕНЬШЕНИЕ ЖЕСТКОСТИ КОРПУСА
Следствием выполнения условия (8.1), уменьшающим упругость корпуса судна до эффективной и энергетически наивыгоднейшей, является уменьшение жесткости корпуса.
В общем виде жесткость $k$ тела есть отношение сжимающей силы $F$ к величине линейной деформации $\Delta l$ сжатия тела в виде формулы
\( k =\frac{F}{\Delta l}\); (9.1)
Ускорение $G$ судна от действия движущей силы $F$ при массе судна $M$, по второму закону Ньютона, равно
\( G =\frac{F}{M}\); (9.2)
Приращение скорости судна за время его оседлости $T$ при ускорении $G$, равно
\( \Delta \upsilon = GT\); (9.3)
Линейная деформация $\Delta l$ сжатия корпуса нарастает во времени с постоянной скоростью $\Delta \upsilon$ по (9.3) и за время его оседлости T становится равной
\( \Delta l = GT^{2}\); (9.4)
Подставляя в (9.1) сжимающую силу из (9.2) в виде
\( F = MG\); (9.5)
а $\Delta l$ в виде (9.4), после сокращений получена формула жесткости корпуса воздушного судна в виде
\( k =\frac{M}{T^{2}}\); (9.6)
Выполнением условия (8.1) жесткость корпуса воздушного судна уменьшается до эффективной жесткости
\( k_{эф} =\frac{M}{T_{эф}^{2}}\); (9.7)
Отношение (9.6) к (9.7) показывает, во сколько раз надо уменьшить жесткость корпуса воздушного судна, чтобы у него в полете нейтрализовалось лобовое сопротивление, по формуле
\(\frac{k}{k_{эф}} =\frac{T_{эф}^{2}}{T^{2}}\); (9.8)
Подставляя в (9.8) $T_{эф}$ по (8.2) и T по (6.8), после сокращений на $l_{ц}$, соотношение жесткостей принимает вид
\(\frac{k}{k_{эф}} =\frac{4c^{2}}{a^{2}}\); (9.9)
Для Ил-96 скорость звука по корпусу $c = 1071.43м/с$, из таблицы 1, п.21, поэтому, следуя (9.9), для нейтрализации лобового сопротивления у Ил-96, жесткость его корпуса следует уменьшить в 51 раз
\(\frac{k}{k_{эф}} = 4⋅\left(\frac{1071.43^{2}}{300}\right)^{2} = 51раз\); (9.10)
9.2. УСТРОЙСТВО УМЕНЬШЕНИЯ ЖЕСТКОСТИ
Следуя [4], уменьшение жесткости корпуса воздушного судна достигается установкой между носовой частью корпуса и его цилиндрической частью упругой вставки необходимой эффективной жесткости.
Для этого (рис. 9) носовую часть корпуса 1 отделяют от цилиндрической части 2, заменяя жесткое соединение этих частей подвижным, втулочно-пальцевым соединением.
Носовую часть корпуса соединяют с цилиндрической частью стержнем 3 из оргстекла, представляющим указанную упругую вставку необходимой эффективной жесткости.

Рис. 9. Схема монтажа упругой вставки
Пальцы втулочно-пальцевого соединения (рис.10) в виде стержней 4 из металла, выходящие с расчетным шагом из торцевой грани корпуса носовой части, входят с зазором свободного скольжения во втулки 5 того же диаметра, вмонтированные в корпус его цилиндрической части.
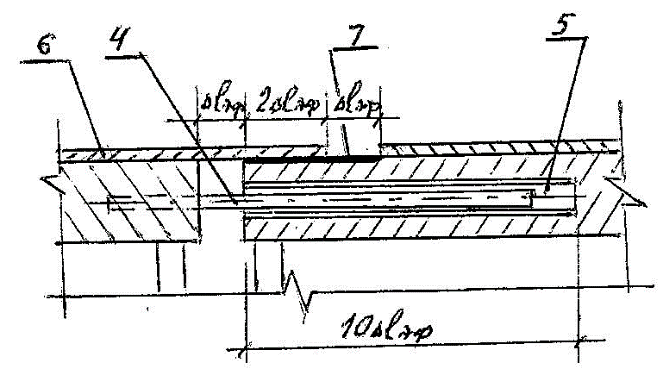
Рис. 10. Узел А пальцево-втулочного соединения частей корпуса
Стержни 4 пальцево-втулочного соединения воспринимают поперечные усилия, возникающие в плоскости корпуса между носовой и цилиндрической его частями.
Носовое покрытие из листового металла 6, для герметичности соединения перепускается на цилиндрическую часть корпуса с нанесением на основание под него слоя 7 герметика со свойствами сальниковой набивки.
Для придания стержню из оргстекла поперечной жесткости и защиты от механических повреждений, он помещается в защитный кожух из металлических труб (рис.11) того же диаметра с зазором свободного скольжения, соединяемых муфтой 8 с одним ее подвижным концом, в виде компенсатора деформации сжатия стержня периодическим действием на него сжимающей силы, движущей силы $F$, с частотой
\( \nu_{эф} =\frac{1}{T_{эф}}\); (9.11)
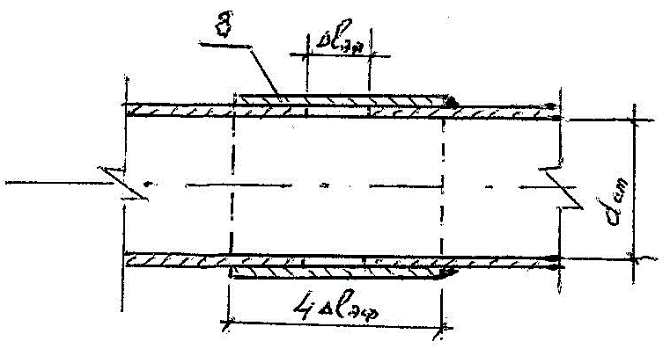
Рис. 11. Узел Б соединения труб защитного кожуха
9.3. РАСЧЕТ УПРУГОЙ ВСТАВКИ
При массе воздушного судна $M$ и эффективном его времени оседлости $T_{эф}$ по (8.2), эффективная жесткость корпуса определяется формулой (9.7).
Из закона Гука жесткость упругой вставки стержня из оргстекла выражается формулой
\( k_{ст} =\frac{EA_{n}}{l_{ст}}\); (9.12)
где $A_{n}$ – площадь поперечного сечения стержня при следующих физико-механических свойствах оргстекла:
\( E = 3⋅10^{3}МПа\) – модуль упругости оргстекла;
\( \sigma_{в} = 70МПа\) – предел прочности оргстекла;
\( R_{y} = 0.3\sigma_{в} = 21МПа\) – расчетное сопротивление оргстекла, принято на 40% меньше из-за ударно-дискретного характера действия сжимающей силы в виде движущей силы F.
Площадь сечения стержня из оргстекла при сжимающей силе (8.12) определяется формулой
\( A_{n} =\frac{F}{R_{y}}\); (9.13)
При известной площади сечения стержня, его диаметр определяется формулой
\( d_{ст} =\sqrt{\frac{4A_{n}}{\pi }}\); (9.14)
Приравниваем (9.12) и (9.7),
\(\frac{EA_{n}}{l_{ст}} =\frac{M}{T_{эф}^{2}}\); (9.15)
Из (9.15) длина стержня упругой вставки определяется формулой
\( l_{ст} =\frac{EA_{n}T_{эф}^{2}}{M}\); (9.16)
9.4. РЕКОМЕНДАЦИИ КОМПОНОВКИ ПОМЕЩЕНИЙ
Для разгрузки втулочно-пальцевого соединения носовой и цилиндрической частей корпуса, а также предупреждения возможного отрицательного воздействия на организм пилотов гипернизкой, до 3 Гц, частоты (9.11) приложения движущей силы, снижающейся от частоты ее приложения у дозвуковых воздушных судов, равной
\( \nu_{уд} =\frac{1}{T}\); (9.17)
рекомендуется кабину управления пилотов убрать из носовой части воздушного судна, выделив под нее место в голове пассажирского салона и оснастив ее искусственным зрением, «виртуальными окнами».
Панорамный наружный вид проецируется на экраны, а сама кабина лишена привычных иллюминаторов и окон остекления.
Видеокамеры размещаются в стратегически важных местах на носовой поверхности лайнера и боковых поверхностях, примыкающих к носовой части.
Необходимое количество видеокамер фиксируют события вокруг лайнера в пространстве 360°, а изображения отображаются на дисплеях кабины пилотов в режиме реального времени.
9.5. РАСЧЕТ ПРЕВРАЩЕНИЯ ВОЗДУШНЫХ СУДОВ В СВЕРХЗВУКОВЫЕ
По приведенным формулам аэродинамики выполнены расчеты превращения воздушных судов Ил-96-300 и Ил-86 в сверхзвуковые лайнеры за счет нейтрализации у них в полете лобового сопротивления. По результатам расчета основные характеристики лайнеров сведены в таблицы 2 и 3.
Таблица 2
Основные характеристики Ил-96-300, как сверхзвукового
Характеристика | Авиалайнер Ил-96-300 | ||
Серийный | Сверхзвуковой | ||
| 1. Мощность двигателей, N; | кВт | 1.52·105 | 1.52·105 |
| 2. Масса взлетная, M; | т | 250 | 250 |
| 3. Крейсерская скорость, $\upsilon ;\upsilon_{эф}$; | м/с | 241.67 | 645.89 |
| км/ч | 870.00 | 2325.2 | |
| 4. Движущая сила, F; | кН | 627.84 | 235.33 |
| 5. Сопротивление трения, Fтр; | кН | 87.90 | 235.00 |
| 6. Доля сопрот. трения, \(\frac{F_{тр}}{F};\ | % | 14.00 | 100 |
| 7. Лобовое сопротивление, Fлоб; | кН | 520.47 | 0.00 |
| 8. Доля лобового сопрот., \(\frac{F_{лоб}}{F};\) | % | 83.0 | 0.00 |
| 9. Ускорение, \( G =\frac{F}{M}\); | м/с2 | 2.51 | 0.94 |
| 10. Разгонное число, $n_{0}$; | 2192 | 2192 | |
| 11. Время оседлости, $T;T_{эф};$ | с | 0.0439 | 0.3136 |
| 12. Частота ударов дв. силы, $\nu_{уд};\nu_{эф};\left(\frac{1}{T}\right)$; | Гц | 22.78 | 3.19 |
| 13. Разгонное время, \( t;t_{эф};\left(n_{0}T\right)\); | с | 96.23 | 687.41 |
| 14. Разгонный путь, \( S;S_{эф};\left(\frac{Gt^{2}}{2}\right)\); | км | 11.62 | 222.10 |
| 15. Жесткость корпуса, k; | Н/м | 1.3·108 | 2.54·106 |
| 16. Деформация сжатия корпуса, \( \Delta l = GT^{2}\) | мм | 4.84 | 92.4 |
| Упругая вставка, стержень из оргстекла | |||
| 17. Диаметр, dст; | мм | – | 119.4 |
| 18. Длина, lст; | м | – | 13.22 |
| 19. Площадь крыла, S; | м2 | 353.9 | 370.17 |
Таблица 3
Основные характеристики Ил-86, как сверхзвукового
Характеристика | Авиалайнер Ил-86 | ||
Серийный | Сверхзвуковой | ||
| 1. Мощность двигателей, N; | кВт | 1.23·105 | 1.23·105 |
| 2. Масса взлетная, M; | т | 208 | 208 |
| 3. Крейсерская скорость, $\upsilon ;\upsilon_{эф}$; | м/с | 241.67 | 603.25 |
| км/ч | 870.00 | 2171.70 | |
| 4. Движущая сила, F; | кН | 510.12 | 203.90 |
| 5. Сопротивление трения, Fтр; | кН | 81.47 | 203.77 |
| 6. Доля сопрот. трения, \(\frac{F_{тр}}{F};\) | % | 16.00 | 100 |
| 7. Лобовое сопротивление, Fлоб; | кН | 434.93 | 0.00 |
| 8. Доля лобового сопрот., \(\frac{F_{лоб}}{F}\); | % | 85.3 | 0.00 |
| 9. Ускорение, \( G =\frac{F}{M}\); | м/с2 | 2.45 | 0.98 |
| 10. Разгонное число, $n_{0}$; | 1825 | 1825 | |
| 11. Время оседлости, $T;T_{эф};$ | с | 0.054 | 0.3372 |
| 12. Частота ударов дв. силой, $\nu_{уд};\nu_{эф};\left(\frac{1}{T}\right)$; | Гц | 18.52 | 2.97 |
| 13. Разгонное время, \( t;t_{эф};\left(n_{0}T\right)\); | с | 98.55 | 615.39 |
| 14. Разгонный путь, \( S;S_{эф};\left(\frac{Gt^{2}}{2}\right)\); | км | 11.90 | 185.60 |
| 15. Жесткость корпуса, k; | Н/м | 7.13·107 | 1.83·106 |
| 16. Деформация сжатия корпуса, \( \Delta l = GT^{2}\) | мм | 7.14 | 111.43 |
| Упругая вставка, стержень из оргстекла | |||
| 17. Диаметр, dст; | мм | – | 111.2 |
| 18. Длина, lст; | м | – | 15.92 |
| 19. Площадь крыла, S; | м2 | 320 | 353.06 |
ВЫВОДЫ
- Приведенные формулы аэродинамики главных аэродинамических коэффициентов $C_y$ и $C_x$, крейсерской скорости полета, лобового сопротивления, площади крыла и оптимальной взлетной массы воздушного судна могут использоваться для аналитического расчета необходимой мощности силовых установок при проектировании и создании нового типа воздушных судов.
- Основная часть сопротивления полету авиалайнера, более 80 процентов, сосредоточена в лобовом сопротивлении, природа которого заключена в различии упругости корпуса судна и упругости воздушной среды.
- Эффективность полета воздушных судов, рентабельность повышается в семь раз, пропорционально квадрату увеличения крейсерской скорости полета (2,67 раза) без увеличения тяги двигателей за счет нейтрализации лобового сопротивления путем искусственного изменения упругости корпуса авиалайнера упругой вставкой между носовой и цилиндрической частью корпуса.
- На действующих воздушных судах нейтрализация лобового сопротивления и перевод их в сверхзвуковой режим полета без слоя сжатого воздуха перед ними в виде ударной волны, достигается путем их реконструкции для монтажа на корпусе упругой вставки по изобретению, патент РФ №2397101.

.png&w=640&q=75)