Пусть задана ориентированная двухполюсная сеть с вершинами 1, 2, …, n, в которой вершина 1 – источник, вершина n – сток, весовые коэффициенты дуг – их пропускные способности. Тогда максимальная пропускная способность сети находится алгоритмом расстановки меток [1], содержащем 6 шагов, в том числе, такие шаги как «откат назад» и «определение остаточной сети». Предлагается более простой алгоритмом, назовем его алгоритмом кратчайших путей.
Шаг 1. Считая весовые коэффициенты дуг их длинами, находится кратчайший путь из вершины 1 в вершину n, применяя алгоритм Дейкстры или какой-либо другой метод.
Шаг 2. Наименьший из весовых коэффициентов дуг полученного пути, а это максимальная пропускная способность пути, вычитается из длин всех дуг этого пути и дуги с весом 0 из рассмотрения исключаются.
Шаг 3. Если нет пути из вершины 1 в вершину n, то останов, максимальная пропускная способность сети равна сумме максимальных пропускных способностей полученных путей, иначе на шаг 1.
Задача 1. Применяя алгоритм кратчайших путей, найти максимальную пропускную способность сети, показанной на рисунке 1.
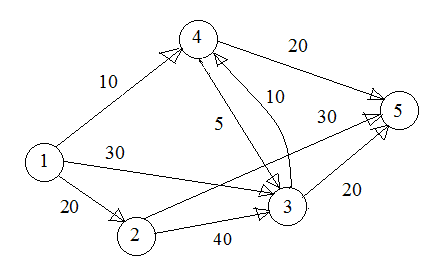
Рис. 1. Сеть задачи 1
1. Кратчайший путь из 1 в 5 это 1→4→5.
2. Минимум весовых коэффициентов пути равен 10, то есть максимальная пропускная способность пути Σ1=10, принимается с(1, 4)=10-10=0, с(4, 5)=20-10=10, сеть упрощается (рис. 2).
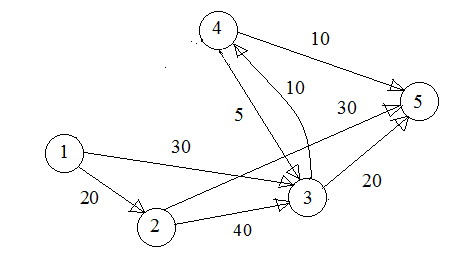
Рис. 2. 1-й промежуточный вид сети задачи 1
3. Теперь кратчайший путь 1→3→4→5.
4. Минимум весовых коэффициентов пути равен 10, то есть максимальная пропускная способность пути Σ2=10, принимается с(1, 3)=30-10=20, с(3, 4)=10-10=0, с(4, 5)=10-10=0, сеть упрощается (рис. 3).
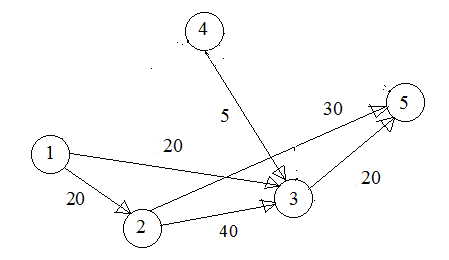
Рис. 3. 2-й промежуточный вид сети задачи 1
5. Кратчайший путь 1→3→5.
6. Минимум весовых коэффициентов пути равен 20, то есть максимальная пропускная способность пути Σ3=20, принимается с(1, 3)=20-20=0, с(3, 5)=20-20=0, сеть упрощается (рис. 4).
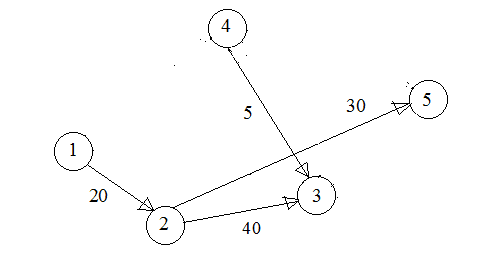
Рис. 4. 3-й промежуточный вид сети задачи 1
7. Путь из 1 в 5 один 1→2→5.
8. Минимум весовых коэффициентов пути равен 20, то есть максимальная пропускная способность пути Σ4=20, принимается с(1, 2)=20-20=0, с(2, 5)=30-20=0. Так больше нет путей из 1 в 5, то максимальная пропускная способность сети Σ=10+10+20+20=60.
Задача 2. Применяя алгоритм кратчайших путей, найти максимальную пропускную способность сети, показанной на рисунке 5.
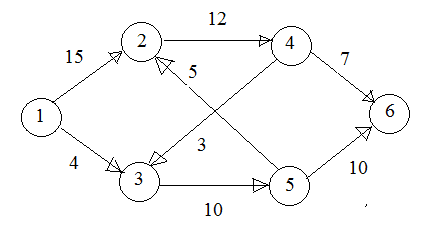
Рис. 5. Сеть задачи 2
1. Кратчайший путь из 1 в 6 это 1→3→5→6.
2. Минимум весовых коэффициентов пути равен 4, то есть максимальная пропускная способность пути Σ1=4, принимается с(1, 3)=4-4=0, с(3, 5)=10-4=6, с(5, 6)=10-4=6, сеть упрощается (рис. 6).
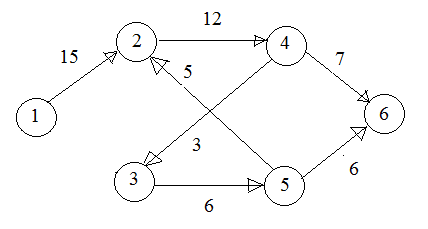
Рис. 6. 1-й промежуточный вид сети задачи 2
2. Теперь кратчайший путь из 1 в 6 это 1→2→4→6.
3. Минимум весовых коэффициентов пути равен 7, то есть максимальная пропускная способность пути Σ2=7, принимается с(1, 2)=15-7=8, с(2, 4)=12-7=5, с(4, 6)=7-7=0, сеть упрощается (рис. 7).
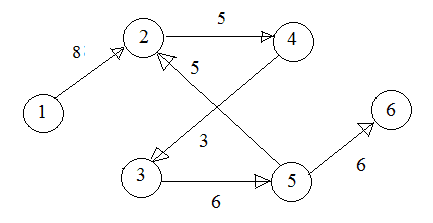
Рис. 7. 2-й промежуточный вид сети задачи 2
4. Кратчайший путь из 1 в 6 один 1→2→4→3→5→6.
5. Минимум весовых коэффициентов пути равен 3, то есть максимальная пропускная способность пути Σ3=3, поэтому максимальная пропускная способность сети Σ=4+7+3=14.

.png&w=640&q=75)