Оригинальный метод исследования динамики бурильной колонны в процессе углубления скважины

Бурение скважины № 500 объединения «Оренбургнефть» в Бузулукском УБР на Бобровском месторождении осуществлялось турбобуром 3ТСШ1-195 длиной 25,7 м с различными длинами УБТ. Вертикальная нагрузка на долото постепенно увеличивалась от 0 до нагрузки, при которой турбобур останавливался. Подача долота осуществлялась регулятором подачи долота РПДЭ-3. При этом регистрировались продольные и поперечные колебания бурильной колонны над ротором. Датчики поперечных колебаний, установленные на ведущей трубе, регистрируют и крутильные колебания. Резонансные частоты фиксировались по увеличению амплитуды гармонических колебаний на фоне прочих колебаний. Частота вращения ротора турбобура измерялась гидротурботахометром ГТН-3М. В таблице приведены исходные данные, результаты измерений и расчётов по рассматриваемой скважине [1].

Таблица

Исходные данные и результаты расчётов параметров стоячих волн при бурении скважины № 500

Для теоретического описания явлений, возникающих в КНБК при образовании стоячих волн, будем её рассматривать как цилиндрический стальной стержень. Если один конец стержня жёстко закрепить, то при возбуждении стоячей волны на собственной частоте на длине стержня уместится нечётное количество четвертей продольной волны. Из курса физики известно, что длина продольной волны (λ), есть расстояние, на которое распространяются продольные колебания в стержне за один период, и находится как произведение скорости распространения колебаний на их период или как частное от деления скорости v на частоту f    .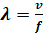

Для описания связанных продольных и крутильных колебаний долота, обусловленных волнообразным забоем, будем рассматривать траекторию движения точки периферийного конца оси вращения шарошки. Эта траектория проходит по цилиндрической поверхности. Траекторию представим развёрткой на плоскость чертежа. Таким образом, в плоскости чертежа мы видим траекторию движения точки долота с некоторой линейной скоростью V, раскладываемой в вертикальном V_В, и в горизонтальном направлении V_Г. На рис. 1 изображена предполагаемая развёртка траектории в течение одного периода колебаний долота.

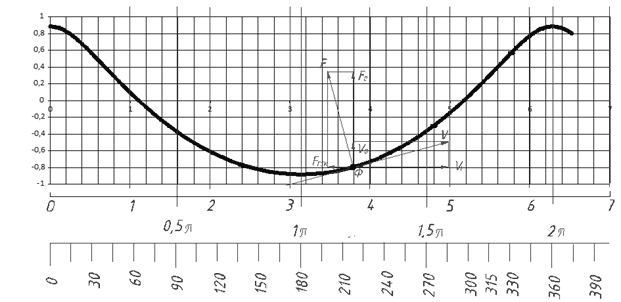
Рис. 1. Развёртка траектории движения периферийного конца оси вращения шарошки долота на вертикальную плоскость

Для выявления условий возникновения резонанса при расчётах расстояние на развёртке, на которое долото смещается по горизонтали, приведём в условных единицах длины (радианах или градусах длины, один градус длины равен 1/360 реального пути за один оборот).

Максимальную возможную амплитуду как вертикальных, так и горизонтальных колебаний примем также равной одной условной единице. Их конкретные значения можно определить, измерив амплитуду вертикальных колебаний, а зная параметры долота (диаметр, угловую амплитуду крутильных колебаний), вычислить истинную амплитуду крутильных колебаний конца оси шарошки.

Вертикальное перемещение долота будем описывать для упрощения только переменной составляющей, так как углубление долота за один оборот мало, в т. ч и по сравнению с горизонтальным перемещением.

Горизонтальное перемещение долота имеет две составляющие: постоянную, определяемую угловой скоростью вращения бурильной колонны и переменную, с частотой крутильных колебаний КНБК.

Переменные составляющие вертикальных и горизонтальных перемещений долота сдвинуты в пространстве и во времени на π/2 (900).

При роторном бурении траектория перемещения периферийного конца оси шарошки на вертикальную плоскость развёртки имеет следующий вид:

Х = аt + bsint,    (1)

Y = ccost,    (2)

где: а – постоянная составляющая горизонтальной скорости, задаваемая ротором (в условных единицах, а = 1; b и c – амплитуды горизонтальных (крутильных) и вертикальных (продольных) колебаний конкретной точки стоячей волны, находящейся на расстоянии L от верхнего конца КНБК.

b = cosL_Г,    (3)

c = cosL_В.    (4)

Численные значения коэффициентов b и c определяются длиной горизонтальной L_Г и вертикальной L_В, волн, размещаемой на длине КНБК и по величине b ≠ c.

Производные от выражений (1) и (2) описывают горизонтальную и вертикальную скорости перемещения долота при условной скорости подачи долота, а = 1:

dX/dt = 1 + bcost,    (5)

dY/dt = - csint.    (6)

Вертикальная скорость долота V_В (dY/dt) имеет только переменную составляющую с частотой продольных колебаний КНБК.

Горизонтальная скорость долота V_Г (dX/dt) имеет две составляющие: постоянную, равную одной условной единице, определяемую угловой скоростью вращения бурильной колонны и переменную с частотой крутильных колебаний КНБК.

Шарошка действует на забой силой, направленной перпендикулярно его поверхности, состоящей из вертикально направленной вниз постоянной составляющей веса бурового инструмента и переменной составляющей, вызванной усилиями, возникающими в КНБК в результате её деформации при продольных колебаниях.

В результате реакции забоя F на наклонном участке на шарошку действуют вертикальная составляющая F_В, и горизонтальная составляющая F_ГСК, выполняющая роль "скатывающей" силы, которая в общем случае уравновешивается силой трения и упругой силой, возникающей при скручивании КНБК. На собственных частотах момент силы трения преодолевается моментом ротора, а момент «скатывающей» силы уравновешивается моментом упругой силы, возникающей при скручивании КНБК.

На рис.1 в точке Ф изображено разложение нормальной реакции забоя F на вертикальную и горизонтальную составляющие. Кроме них изображено разложение скорости шарошки, направленной по касательной к поверхности забоя V на горизонтальную V_Г и вертикальную составляющие V_В.

Из подобия треугольников разложения сил и скоростей следует:

F_ГСК/F_В = V_В/V_Г.    (7)

Для выяснения условий согласования продольных и крутильных колебаний шарошки при резонансе рассмотрен пример с длиной КНБК равной суммарно (четвёртая строка таблицы) трём (нечётное число) четвертям длин волн [2].

Известно:

• скорость продольных волн в стальном стержне 5130 м/с;
• скорость крутильных (сдвиговых) волн 3200 м/с.

Скорость продольных волн в 1,6 раз больше крутильных. Так как скорость крутильной волны в 1,6 раз меньше скорости продольной волны, то на одной и той же длине КНБК укладывается крутильных волн в 1,6 раз больше, чем продольных.

Находим какая часть от суммарных трёх четвертей волн приходится на продольную волну: 3 / 2,6 = 1,154 и выражаем её длину в условных угловых единицах длины 103,85⁰ (1,154 × 90⁰ = 103,85⁰).

Тогда коэффициент амплитуд для вертикальных перемещений точки М (рис. 3) и скоростей V_В составит:

с = cosL_В = cos103,85⁰ = -0,239 для М и V_В, коэффициент амплитуды для вертикальных усилий для F_В сжатия-растяжения:

sinL_В = sin103,85⁰ = 0,971 для F_В.

Количество четвертей крутильных волн составляет:

3 - 1,154 = 1.154 х 1,6 = 1,846 или в угловых единицах 166,15⁰.

Общая длина продольной и крутильной стоячих волн составляет 103,85⁰ + 166,15⁰ = 270⁰, или 3/4 от 360⁰, или (3/4 λ).

Коэффициент амплитуд для горизонтальных перемещений G и скоростей V_Г составляет:

b = cosL_Г = cos166,15⁰ = - 0,971 для G и V_Г.

Коэффициент амплитуды для горизонтальных усилий скручивания-раскручивания:

sinL_Г = sin166,15⁰ = 0,239 для F_Г

Отметим, что модули коэффициентов амплитуд для точек сопряжения волн на долоте попарно равны. Для нечётной суммы четвертей волн это следующие пары:

sinL_В = cosL_Г, (|sin103,85⁰| = |cos166,15⁰ | = 0,971)

cosL_В = sinL_Г, (|cos103,85⁰| = |sin166,15⁰ | = 0,239)

Преобразуем выражение (7), подставив приведённые выше коэффициенты амплитуд для сил и скоростей с учётом постоянных составляющих.

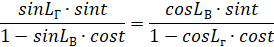
Получаем:

0,239sint/(1 – 0,971cost) = 0,239sint/(1 – 0,971cost)    (8)

Из (8) следует, что для частного случая с длиной КНБК, на которой суммарно длина продольной и крутильной волн равна 3/4 λ на собственных частотах, в каждый момент времени реактивная сила скручивания КНБК уравновешивает скатывающую силу, возникающую от действия вертикальной силы на поверхность забоя. Это справедливо для всех нечётных сумм продольных и крутильных четвертей стоячих волн при роторном бурении.

На рис.2 изображена одна волна, умещающаяся на длине прямого сплошного стержня, состоящая их четырёх четвертей. Все точки стержня перемещаются в направлении его продольной оси. Отложим на этом рисунке длины продольной и крутильной стоячих волн из предыдущего описания.

Тогда точка А соответствует свободному верхнему концу КНБК для продольной волны, а точка Д соответствует верхнему свободному концу для крутильной волны.

Точка Л соответствует нижнему концу продольной волны и определяет перемещение долота по вертикали, а точка М соответствует нижнему концу крутильной волны и определяет перемещение долота по горизонтали. В пространстве перемещения крутильных и продольных колебаний сдвинуты на π/2 (90⁰). На чертеже рис.3 между точками Л и М расстояние также π/2 (λ/4).

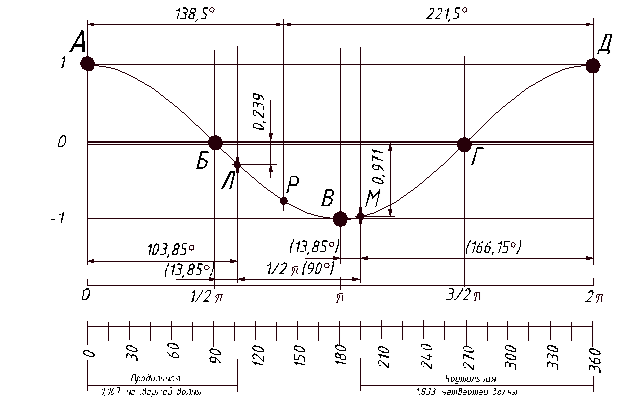
Рис. 2. Форма стоячей волны

Получается, что в точке Л (М) при изменении направления колебаний на π/2, как бы из волны вырезается участок длиной π/2 (то есть четверть волны), как показано на рис.3. Таким образом, на длине КНБК помещается в сумме нечётное число четвертей волн 3/4 λ. При этом обеспечивается согласование импедансов продольной и крутильной волн.

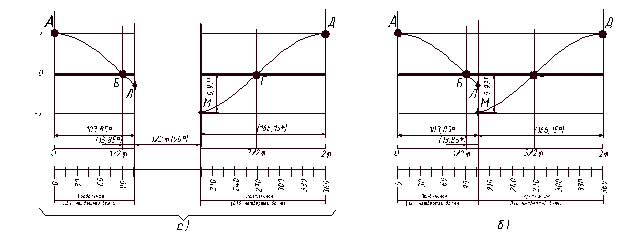
Рис. 3. Распределение смещений по длине стержня

На рис.2 и 3 по оси абсцисс отложена длина КНБК, а по оси ординат – относительная амплитуда отклонений от точки равновесия. Длина КНБК измеряется в «градусах или радианах длины» для удобства расчётов. Например, в точке А (ноль по оси абсцисс) cos0⁰=1, и максимальная относительная амплитуда в этой точке равна единице. В точке В cos(π/2) равен нулю, и амплитуда равна нулю. В точке Л, отстоящей от точки А на расстоянии 103,85 «градусов длины» продольной волны, cos103,85⁰ = (-0,239). Тогда амплитуда вертикальных колебаний долота составляет 0,239 условных единиц (точка Л). В точке Д максимальная относительная амплитуда крутильных колебаний составляет также одну условную единицу. В точке М, отстоящей от точки Д на расстоянии 166,15 «градусов длины» крутильной волны, cos166,15⁰ = (- 0,971), следовательно, в точке М амплитуда крутильных колебаний долота равна 0,971 условных единиц.

Подставив в формулы (1) и (2) вычисленные коэффициенты из (3) и (4) для КНБК с суммой длин волн 3/4 λ получаем координаты истинной траектории движения периферийного конца оси шарошки.

Х = 1t - 0,971sint,    (9)

Y = - 0,239cost,    (10)

где: t – время в относительных единицах.

На рис.4 согласно (9) и (10) построена развёртка траектории в течение одного периода колебаний долота. Долото движется по кривой, форма которой находится между синусоидой и циклоидой.

Смещение долота по горизонтали, приведено в условных единицах. В начале координат долото находится в самой низкой точке траектории. Ромбиками отмечены положения долота через равные промежутки времени. В нижней части траектории скорость скручивания-раскручивания наибольшая и направлена против постоянной составляющей скорости вращения долота, обеспечиваемой вращением ротора (метки времени, отмеченные ромбиками, расположены чаще). В верхней части траектории скорость скручивания-раскручивания совпадает с направлением постоянной составляющей вращения долота ротором (метки времени расположены реже). Здесь же представлена синусоидальная траектория с красными квадратными метками. При синусоидальной траектории отсутствует горизонтальная переменная составляющая (метки времени расположены равномерно по всему графику). На интервале от 0 до π синусоида М пересекает ось абсцисс в точке 1,571 (π/2), а траектория долота (кривая GM) пересекает эту ось в точке 0,600. Разница между ними (1,571 – 0,600 = 0,971) даёт значение амплитуды крутильных колебаний долота в относительных условных единицах. На этом интервале переменная составляющая горизонтального смещения долота имеет отрицательное значение (график находится левее графика синусоиды, долото отстаёт от вращательного перемещения, задаваемого ротором привода вращения буровой установки).

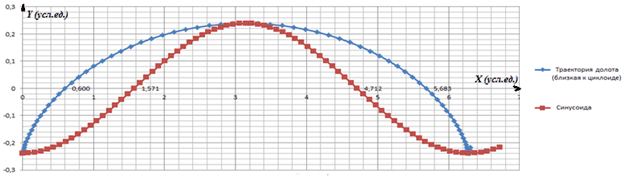
Рис. 4. Развёртка траектории движения периферийного конца оси шарошки при длине КНБК равной в сумме 3/4 λ

На интервале от π до 2π переменная составляющая горизонтального перемещения долота имеет положительное значение (график находится правее графика синусоиды, долото опережает вращательное перемещение, задаваемое ротором привода вращения буровой установки). Это же показано и на рис.7 только в другой системе координат. График G (смещение горизонтальное долота переменное) на интервале от 0 до π (180⁰) имеет отрицательные значения, а на интервале от π (180⁰) до 2π (360⁰) имеет положительные значения.

Рассчитав и подставив приведённые в соотношение (7) реактивные составляющие:

0,239sint / (1 – 0,971cost) = 0,239sint / (1 – 0,971cost).    (11)

Получаем, что в каждый момент времени реактивная сила скручивания КНБК уравновешивает скатывающую силу, возникающую от действия вертикальной силы на поверхность забоя, хотя из (2) следует, что механические импедансы продольной волны,

tg(L_В) = tg103,85⁰ = -4,056

и крутильной волны,

tg(L_Г) = tg166,15⁰ = -0,246

на долоте не совпадают.

Но зато выполняются соотношения (12) и (13) для коэффициентов амплитуды усилий и скоростей:

|sinL_В| = |cosL_Г|, т.е. |sin103,85⁰| = |cos166,15⁰ | = 0,971,    (12)

|cosL_В| = |sinL_Г|, т.е. |cos103,85⁰| = |sin166,15⁰| = 0,239,    (13)

при которых выполняется соотношение (7) согласования импедансов продольной и крутильной волн.

Выводы:

1. Предложенный метод исследования на основе модели КНБК в виде упругого стального стержня показывает, что при определённых соотношениях длины КНБК и частоты колебаний, формируется такая форма поверхности забоя, что на долоте происходит согласование отличающихся между собой импедансов продольных и крутильных волн. При этом на амплитуду вертикальной переменной составляющей нагрузки на долото накладывается ограничение. Она не может быть больше, чем постоянная составляющая (осевая нагрузка на долото), иначе, на участках, где их геометрическая сумма меньше нуля, теряется контакт долота с забоем, колебания перестают быть гармоническими. Аналогичное ограничение накладывается и по скорости крутильных колебаний. Амплитуда переменной составляющей тоже не может быть больше постоянной составляющей. В таких случаях не формируется поверхность забоя, обеспечивающая согласование импедансов продольной и крутильной стоячих волн, приводящих к возникновению резонанса КНБК.
2. Из изложенного выше следует, что при бурении шарошечными долотами ротором существуют определённые соотношения длины КНБК и частоты вращения долота, способствующие образованию стоячих продольных и крутильных волн, приводящих к резонансному режиму. Эти соотношения просчитываются и их необходимо учитывать при практическом бурении для снижения аварийности, в частности в стыковочном узле между ЛБТ и КНБК.