Алгоритм диагностики технических объектов с применением теории случайных процессов

В технических системах изменения или переходы систем в новое состояние часто имеют случайный характер. С помощью стохастических матриц возможных переходов, обладающих определенными свойствами, можно описать цепочку таких переходов. Теория Марковских цепей является инструментом для анализа процессов, в которых переход из одного состояния в другое зависит только от состояния системы в настоящее время и не зависит от того, когда и каким образом система пришла в это состояние. Анализ задач такого типа приводится в работах [1, 2], для экономических систем этот метод более распространен [3]. Алгоритм диагностики рассмотрим на примере оценки ресурса и остаточного ресурса для центробежного насоса.

Для центробежного насоса принимаются следующие состояния:

S₁ – исправное; S₂ – работоспособное при небольших дефектах; S₃ – работоспособное при средних дефектах; S₄ – неисправное, значительные дефекты; S₅ – критическое (необходим капитальный ремонт); S₆ – предельное (дальнейшая эксплуатация невозможна).

Процессы удобно иллюстрировать с помощью графа состояний, где прямоугольниками обозначены состояния системы S, а стрелками – возможные переходы из одного состояния в другое состояние. Против каждой стрелки проставляются соответствующие вероятности перехода p_ij . На графе состояний отмечают также и возможные задержки в прежнем состоянии с помощью «петли», т.е. стрелки, направленной из данного состояния в него же.

При изучении вопроса оценки переходных вероятностей можно применить модель оценки по относительной частоте (таблица 1).

Таблица 1

Оценка вероятности по относительной частоте

Следует отметить широко применяемый метод экспертных оценок, если задача сбора статистических данных оказывается достаточно сложной. В этом методе используется база знаний, накопленных специалистами в соответствующей области.

Целесообразно привести основные соотношения между переходными вероятностями и вероятностями состояний.

Рассмотрим промежуток времени [0,T] и разобьем его на n частей. Считаем, что система переходит из состояния в состояние только в заданные моменты времени t₀, t₁,…,t_n (рис.1).

Рис. 1. Разбиение промежутка времени

Обозначим события A={S(t_k)=S_j} –в период времени [t_k, t_k+1] система находится в состоянии S_j , H_i ={S(t_k-1) = Si} – в период времени [t_k-1, t_k] система находилась в состоянии S_i, i=1,..,m. Это полная группа событий, т.е. система в любой момент времени находится только в одном из заданных состояний.

Введем условные вероятности перехода системы в момент времени t_k из состояния S_i в состояние S_j :

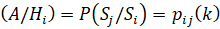     (1)

В момент времени t_k система либо останется в состоянии S_i, либо перейдет в какое-либо другое состояние. Запишем формулу полной вероятности:

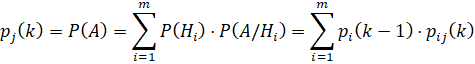.   (2)

Условные вероятности определяется в виде матрицы:

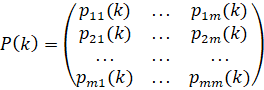.      (3)

Запишем вектор вероятностей состояний в момент времени t_k-1:

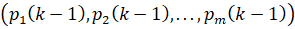.     (4)

При перемножении матрицы (3) и вектора (4), получаем рекуррентную формулу:

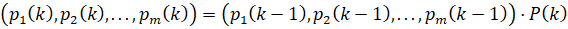.     (5)

Построим модель для диагностики состояния центробежного насоса. Задаем диагностические параметры и принимаем их условные границы (таблица 2).

Таблица 2

Диагностические параметры и возможные состояния центробежного насоса

Перечислим основные диагностические параметры и их влияние на техническое состояние центробежного насоса.

1. Подогрев жидкости в насосе свидетельствует о значительном трении сопрягаемых поверхностей подшипников.
2. Увеличение давления на выходе приводит к повышению нагрузки на корпус насоса.
3. Диаметральный зазор между подшипниками необходим для исключения возможного заедания во время работы агрегата. Он зависит от диаметра вращающихся деталей. Превышение минимального зазора может привести к росту потребляемой мощности, повышенному нагреву подшипников и стойки, задеванию за корпус рабочего колеса, перекосу и задеванию за корпус сальникового уплотнения.
4. Увеличение шероховатости поверхности вала свидетельствует об износе поверхности и увеличенных радиальных вибрациях вала.
5. Чтобы обеспечить хорошую набивку в функционирование уплотнения, а также предотвратить поломку вала и внутреннего износа или заклинивания, и обеспечить необходимую для вала жесткость, прогиб от поверхности корпуса должен быть менее половины минимального диаметрального зазора во всех вкладышах подшипников и изнашиваемых уплотнительных колец.

Схема расположения данных параметров отображена на рис. 2.

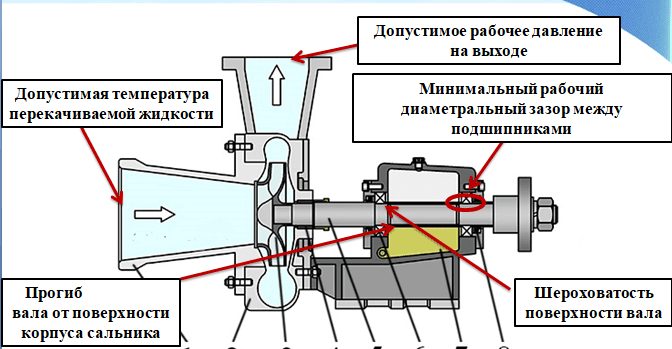
Рис. 2. Схема расположения диагностических параметров

На основе этих данных построим граф состояний (рис. 3). Данный граф описывает возможные переходы системы из одного состояния в другое, а также возможность пребывания в текущем состоянии.

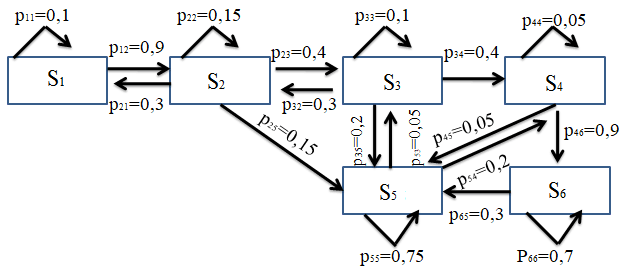
Рис. 3. Граф состояний

Перечислим основные допущения относительно вероятностей переходов:

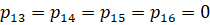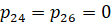1) ; 2) ; 3) .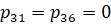

Матрица переходных вероятностей для данного графа принята в виде:

 (9)

Вероятности состояний системы в момент времени t_k определяются по формуле

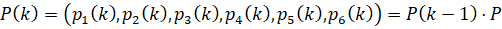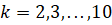, .    (10)

а

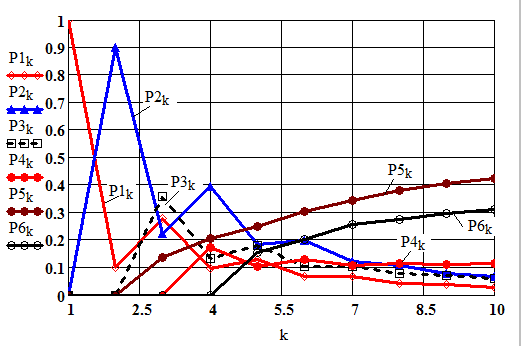
б

Рис. 4. Оценка ресурса центробежного насоса: а) программа в Mathcad; б) изменение вероятностей состояний во времени

В первом случае (рис.4,а) задаем начальным состояние S₁ – система исправна. По графику (рис.4,б) видим, что через k=10 лет с вероятностью p₆+p₅≈0,3+0,4=0,7 система будет находиться в состоянии S₅ или S₆, причем начиная с 2,8 лет этот критерий начинает расти. Таким образом, можно оценить ресурс технического объекта.

Теперь задаем начальное состояние S₄ (рис.5,а). Из этого состояния система будет выходить стремительно, причем с некоторым скачком к состоянию S₆ – предельному (рис.5,б).

а

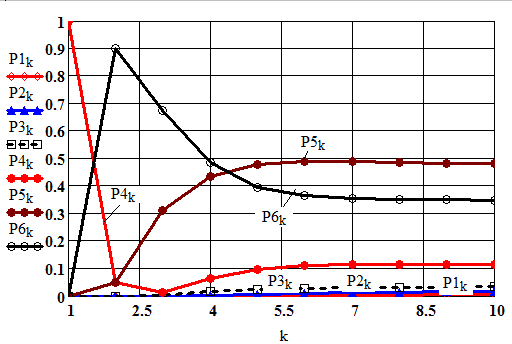
б

Рис. 5. Оценка остаточного ресурса центробежного насоса: а) программа в Mathcad; б) изменение вероятностей состояний во времени

Также видим, что, начиная с 4,6 лет система будет с вероятностью около 0,5 стремиться к состоянию S₅, что говорит о том, что данное состояние будет преобладать в системе, а оно является критическими. Таким образом, динамика вероятностей состояний позволяет оценивать остаточный ресурс насоса.

Наличие скачкообразного изменения вероятностей связано с дискретным временем. Целесообразно рассмотреть процесс с непрерывным временем. Для вычисления плотностей потоков событий λ_i,j воспользуемся формулой

.

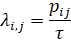Формулируем начальную задачу с системой дифференциальных уравнений Колмогорова и решаем задачу в системе Mathcad методом Рунге-Кутта (рис.6,а). Графики решений показаны пунктирными линиями (рис. 6,б).

а

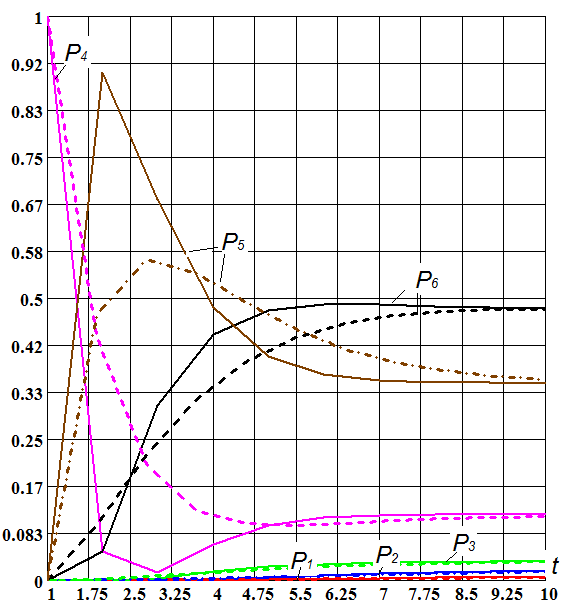
б

Рис. 6. Решение задачи с непрерывным временем

Близость вероятностей состояний для дискретного и непрерывного времени свидетельствует о корректности выбранных алгоритмов.

Заключение

1. Показана принципиальная возможность оценки с некоторой вероятностью ресурса и остаточного ресурса центробежного насоса с помощью определения диагностических параметров и применения теории Марковских цепей.
2. Для построения матрицы переходных вероятностей предложен алгоритм с использованием статистических данных и метода экспертных оценок.
3. Контроль результатов прогноза ресурса предлагается осуществлять переходом к случайному процессу с непрерывным временем для применения системы уравнений Колмогорова.