Задачи обеспечения надежного уплотнения центробежных насосов остаются актуальными, особенно если утечки агрессивной жидкости приводят к большим экологическим и экономическим проблемам. Одними из наиболее перспективных считаются торцевые уплотнения (рис.1). Моделированию динамики торцевых уплотнений посвящены работы ряда исследователей [1-4]. В основном авторы работ рассматривали дискретные модели и определялись характеристики собственных колебаний при наличии осевых нагрузок со стороны вала насоса. Представляет интерес динамика изменения характеристик уплотнения в случае нелинейной зависимости сопротивления между подвижным и неподвижным уплотнительными кольцами. При этом важно вычислять зазор, уменьшение или увеличение которого приводит к потере работоспособности уплотнения.
На рис. 2 показана расчетная схема торцевого уплотнения.
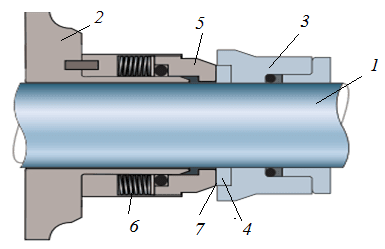
Рис. 1. Схема торцевого уплотнения: 1 – вал насоса; 2 – корпус насоса; 3 – гильза; 4 – вращающееся уплотнительное кольцо; 5 – неподвижное уплотнительное кольцо; 6 – пружина, 7 – зазор между кольцами
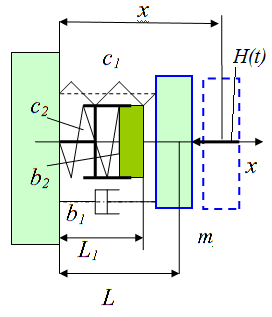
Рис. 2. Расчетная схема осевых колебаний торцевого уплотнения: m – масса подвижного кольца, x(t) – перемещение подвижного кольца, L – положение равновесия
Коэффициент упругого сопротивления определяется по формуле
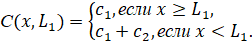 (1)
(1)
где c1, c2 – коэффициенты упругого сопротивления жидкости в зазоре и пружины.
Диссипативное сопротивление также нелинейно зависит от перемещения
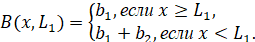 (2)
(2)
Здесь b1, b2 – коэффициенты, учитывающие демпфирование жидкости и трение элементов уплотнения. Уравнение движения дискретного элемента, с учетом осевой нагрузки H(t), и начальные условия имеют вид
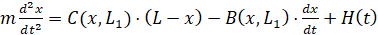 ,
, 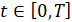 , (3)
, (3)
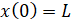 , (4)
, (4)
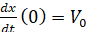 . (5)
. (5)
Величина рабочего зазора δ(t) между кольцами определяется по формуле
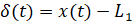 . (6)
. (6)
Начальная задача для дифференциального уравнения второго порядка сводится к начальной задаче для системы двух уравнений первого порядка:
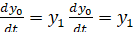 ,
, 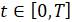 , (7)
, (7)
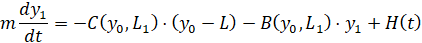 , (8)
, (8)
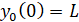 , (9)
, (9)
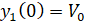 . (10)
. (10)
Основные параметры, определяющие жесткое и диссипативное сопротивления представлены на рис. 3. Скачок коэффициентов сопротивления имитирует контактное взаимодействие уплотнительных колец.
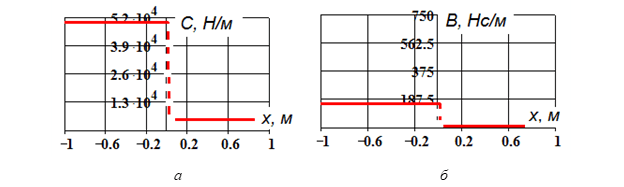
Рис. 3. Основные параметры, определяющие жесткое и демпфирующее сопротивление:
c1=5000 H/м; c2=50000 Н/м; m=0,8кг; b1=10 Нс/м; b2=150 Нс/м; L=0,02 м; L1=0,019 м
Решение начальной задачи находится с помощью встроенных функций системы Mathcad. Для сравнения приводится решение, при котором жесткое сопротивление не зависит от перемещения.

а
б
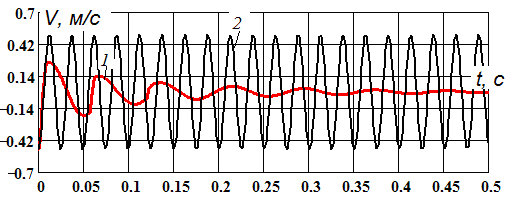
Рис. 4. а) Реализация метода Рунге-Кутта в системе Mathcad; б) Скорость дискретного элемента: (1) при наличии нелинейного сопротивления; (2) при наличии линейного сопротивления
В целях тестирования численного метода рассмотрим начальную задачу с уравнением движения, в котором учитывается только нелинейное жесткое сопротивление
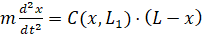 ,
, 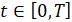 , (11)
, (11)
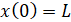 , (12)
, (12)
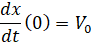 . (13)
. (13)
Выполним подстановку , тогда получим задачу
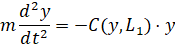 , (14)
, (14)
y0=0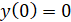 , (15)
, (15)
0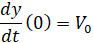 . (16)
. (16)
Подстановкой 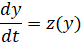 понижается порядок уравнения, в результате получаем уравнение первого порядка с разделяющимися переменными
понижается порядок уравнения, в результате получаем уравнение первого порядка с разделяющимися переменными
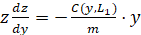 .
.
После интегрирования и обратной замены получаем
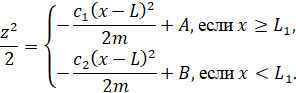 (18)
(18)
Постоянные А и В находятся из начальных условий и условия непрерывности скорости при x=L1.
Аналитическое решение при наличии только жесткой составляющей имеет вид
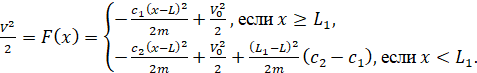
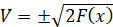 . (19)
. (19)
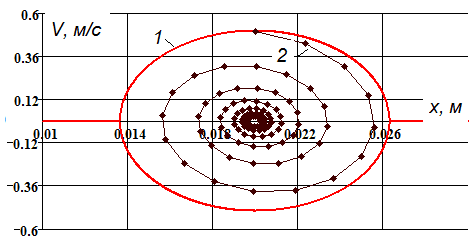
Сравнение решений в фазовых координатах показано на рис.5,а. На рис.5,б приведено изменение по времени величины зазора при начальной импульсной нагрузке.
а
б
Рис. 5. а) Сравнение аналитического решения без демпфирования (1) и численного решения с демпфированием (2); б) Изменение величины зазора при начальном импульсе
Постоянно действующая импульсная осевая нагрузка определялась формулой
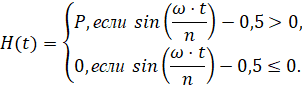 (20)
(20)
Параметры P,ω,n позволяют менять амплитуду и частоту колебаний осевой силы. На рис. 6 показана импульсная нагрузка и колебания скорости подвижного уплотнительного кольца.
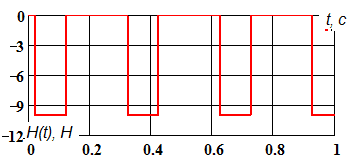
а
б
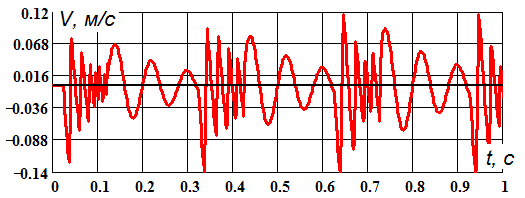
Рис. 6. а) Импульсная нагрузка б) Колебание скорости подвижного кольца
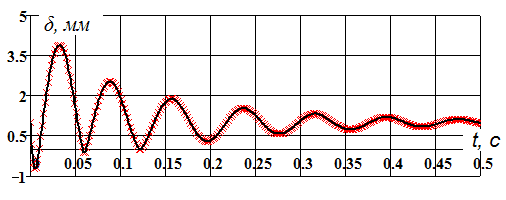
На рисунке 7 показаны колебания величины зазора при постоянно действующей импульсной осевой нагрузке со стороны вала насоса.
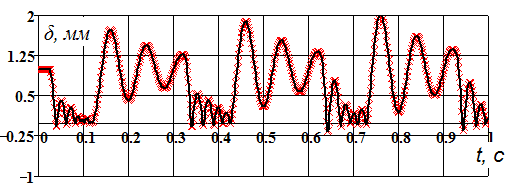
Рис. 7. Колебания зазора при импульсной осевой нагрузке
Заключение
- Применение одномассовой модели с учетом нелинейного сопротивления позволяет получить основные характеристики колебательного процесса элементов торцевого уплотнения при различных характеристиках жесткости и диссипации.
- Получено аналитическое решение начальной задачи в координатах «скорость-перемещение», что позволило сравнить это решение с численным решением и, таким образом, обосновать достоверность численного метода.
- Решение начальной задачи найдено при двух типах осевых нагрузок: осевом начальном импульсе и периодическом осевом импульсе, частота и амплитуда которого моделируются специально заданной функцией.

.png&w=640&q=75)