Цель работы – выполнить аппроксимацию зависимости расходов от уровней в гидрометрическом створе р. Ия – г. Тулун в виде аналитического выражения в форме параболы В. Г. Глушкова. Известно, что для подсчета стока и определения ежедневных расходов воды используются кривые расходов, которые служат графическим представлением зависимости наблюденных расходов и уровней воды в конкретном гидростворе. Указанная выше связь расходов и уровней определяется в результате совокупности многократных дискретных измеренных уровней и расходов воды в конкретном гидрометрическом створе [2].
Для автоматизации процесса подсчета стока и производства расчетов ежедневных расходов воды необходимо представить кривую расходов в виде аналитического выражения. Как правило, для аппроксимации кривой расходов используют или параболу Глушкова, или полиномиальную зависимость. Парабола Глушкова в целом показывает хорошее натурным данным и была выбрана в качестве аналитического выражения в рамках данной работы.
Русло р. Ии в створе гидропоста г. Тулуна, расположенного в Иркутской области, соответствует условиям наличия однозначной зависимости между расходом и уровнем воды, при которой одному конкретному уровню соответствует одно конкретное значение расхода воды. Кривая расхода, устанавливающая в графическом виде связь между расходами и уровнями воды, в гидрометрическом створе поста р. Ия – г. Тулун представлена на рис. а. Данная кривая получена по измеренным расходам в заданном гидростворе и экстраполирована вверх с применением способа «по элементам расхода». Способ состоит в том, что до требуемого уровня достраивается кривая площадей, которая в данной работе построена с применением данных радиолокационной топографической съемки SRTM (Shuttle radar topographic mission) [1] и показана на рис. б. Кривая средних скоростей в рамках исследования экстраполирована до требуемых значений по линейному уравнению, определенному средствами MS Excel (см. рис. в). Расход воды определяется как произведение площади поперечного сечения и средней скорости при конкретном уровне.
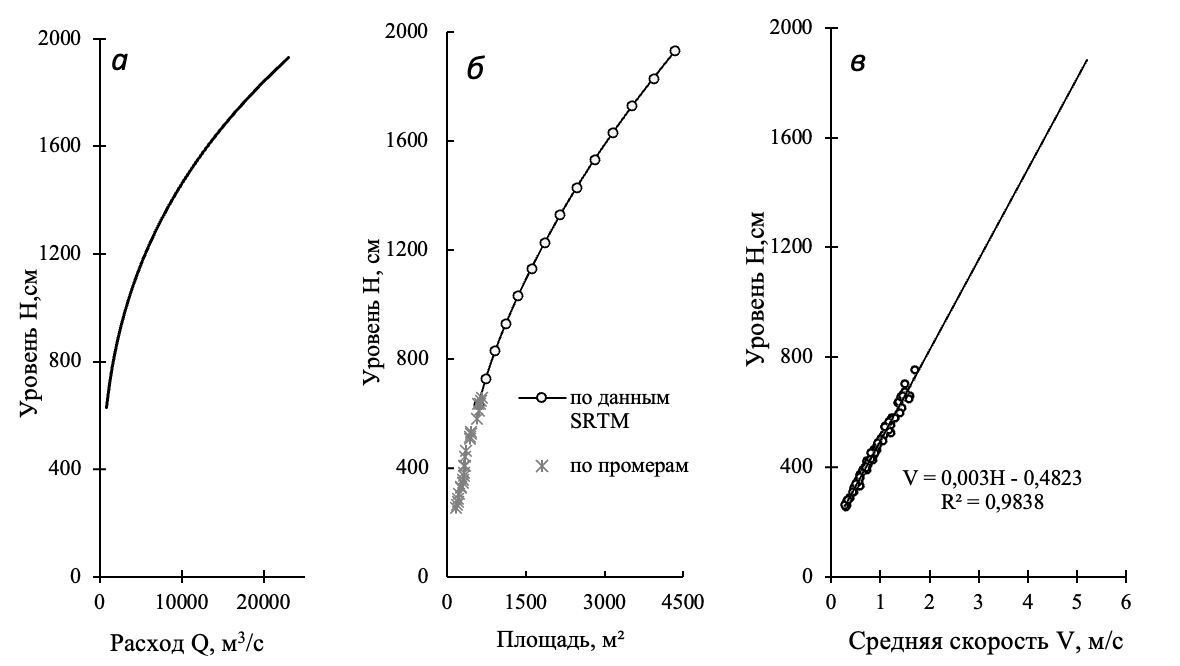
Рис. Кривые расхода (а), площадей (б), средних скоростей (в) в створе гидропоста р. Ия – г. Тулун
В ходе работы для аппроксимации кривой расходов использована парабола Глушкова, выражающая зависимость расходы от уровня в следующеи виде [2]:
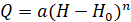 , (1)
, (1)
где Q – расход воды, м³/с; H – наблюденный уровень воды, см; H0 – уровень нулевого расхода, при котором расход воды в данном створе равен нулю, см; и n – параметры уравнения, определяемые в рамках работы по опорной кривой расходов (см. рис. а).
Как правило, отметка нуля графика гидропоста не соответствует уровню нулевого расхода. Отметка нулевого расхода может быть определена по результатам промерных работ, но ее определение на практике бывает затруднено и требует привлечения дополнительных морфометрических материалов, которые часто оказываются недоступными без выполнения дополнительных полевых работ. В этом случае уровень нулевого расхода находится аналитически путем решения системы уравнений, написанных для трёх точек: одной, расположенной в нижней части кривой расходов (Q1; H1), второй - в верхней части (Q2; H2). Абсциссу третьей точки находят как 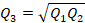 и по ней c кривой расхода находится ордината H3. Из этих соображений находят уровень нулевого расхода как:
и по ней c кривой расхода находится ордината H3. Из этих соображений находят уровень нулевого расхода как:
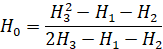 . (2)
. (2)
В таблице (табл. 1) приведены координаты точек 1-3 и по формуле (1) получено значение нулевого расхода, равное 9 см.
Таблица 1
Координаты точек 1-3 для определения уровня нулевого расхода
|
№ точки |
Расход воды Q, м3/с |
Уровень воды H, см |
|---|---|---|
|
1 |
841 |
629 |
|
2 |
23060 |
1929 |
|
3 |
4404 |
1100 |
После этого методом наименьших квадратов ведётся определение параметров параболы Глушкова a и n. Для этого вычисляются следующие определители матриц:
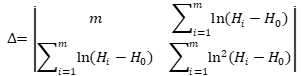 ; (3)
; (3)
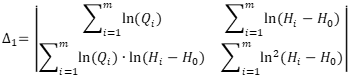 ; (4)
; (4)
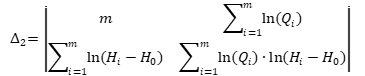 . (5)
. (5)
По методу Крамера находим a и n:
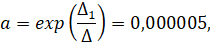 (6)
(6)
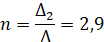 ю (7)
ю (7)
Проведем оценку средней вероятной ошибки построения кривой расходов в форме таблицы (табл. 2) путем сопоставления с координатами опорной кривой расходов (см. рис. а).
Таблица 2
Проверка ошибки аппроксимации кривой расходов аналитической зависимостью по формуле Глушкова
|
№ расхода |
H, см |
Q1, м3/с по опорной кривой расходов |
Q2, м3/с по формуле Глушкова |
ΔQ, м3/с |
Δσ, % |
Δσ2, (%)2 |
|---|---|---|---|---|---|---|
|
1 |
629 |
841 |
817 |
-23 |
-2,9 |
8,2 |
|
2 |
729 |
1272 |
1270 |
-2 |
-0,2 |
0,0 |
|
3 |
829 |
1846 |
1863 |
17 |
0,9 |
0,9 |
|
4 |
929 |
2589 |
2616 |
27 |
1,0 |
1,0 |
|
5 |
1029 |
3518 |
3546 |
29 |
0,8 |
0,6 |
|
6 |
1129 |
4647 |
4672 |
25 |
0,5 |
0,3 |
|
7 |
1229 |
5996 |
6012 |
16 |
0,3 |
0,1 |
|
8 |
1329 |
7575 |
7584 |
9 |
0,1 |
0,0 |
|
9 |
1429 |
9405 |
9415 |
10 |
0,1 |
0,0 |
|
10 |
1529 |
11512 |
11506 |
-6 |
-0,1 |
0,0 |
|
11 |
1629 |
13914 |
13882 |
-32 |
-0,2 |
0,1 |
|
12 |
1729 |
16634 |
16562 |
-72 |
-0,4 |
0,2 |
|
13 |
1829 |
19687 |
19563 |
-124 |
-0,6 |
0,4 |
|
14 |
1929 |
23060 |
22903 |
-157 |
-0,7 |
0,5 |
|
σ, % |
0,6 | |||||
Аппроксимация кривой формулой Глушкова отклоняется от опорной кривой расхода на 0,6 %. Также полученная аппроксимация проверена путем сопоставления с эталонной кривой, за которую в рамках работы принята кривя расходов по многолетним данным, составленная в Иркутском управлении по гидрометеорологии и мониторингу окружающей среды, на участке, освященный данными натурных измерений расходов. Среднее вероятное отклонение от эталонной кривой, составляет 4,0 %, как и у опорной кривой, экстраполированной способом «по элементам расхода». Результаты работы демонстрируют возможность использования полученного аналитического выражения в практическом приложении.

.png&w=640&q=75)