Физическая причина убыточности судов морречфлота и авиалайнеров воздушного флота, и способ кратного увеличения их рентабельности

ВВЕДЕНИЕ

Несовершенство эмпирического метода познания законов движения тел в жидкой среде, под которой подразумеваются вода и воздух, является причиной и следствием несовершенства современных транспортных средств, перемещающих полезные грузы в жидкой среде – судов морречфлота и авиалайнеров воздушного флота.

Корень несовершенства кроется в нерационально большом объеме потребляемого топлива, при весьма небольшой скорости движения для такого объема топлива.

Результатом несовершенства, следствием, является низкая, на грани убыточности рентабельность транспортных средств, когда стоимость топлива на транспортировку груза становится соизмеримой с доходом от стоимости транспортных услуг.

Сущность несовершенства техники, как перерасход топлива над рациональным его потреблением, является причиной известной беды, сопровождающей судоходную отрасль экономики и Аэрофлот, – банкротство судоходных компаний и авиакомпаний, что ложится налоговым бременем на госбюджет в виде дотаций и субсидий для транспортных компаний.

Самая большая беда, кроме экономических потерь – это гибель людей, – экипажей транспортных средств и их пассажиров.

Стремление повышения рентабельности транспортной техники вынуждает ее владельцев идти на нарушения технических норм ее эксплуатации. Командам судов морречфлота допускается идти на перегруз судов, уменьшая нормативный запас их плавучести. Экипажам авиалайнеров, ради экономии топлива, не рекомендуют без особой нужды уходить на запасной аэродром из-за штормовой погоды в порту назначения, или покидать трассу полета для облета грозовых облаков, встреченных на пути полета.

Известны резонансные катастрофы на воде и в воздухе.

Теплоход «Булгария», 2011 год, Куйбышевской вдхр., перегруз судна, каюты на 150 мест расширены до 200 мест за счет служебных помещений, погибло 122 человека.

Траулер «Дальний восток», 2015 год, Охотское море, перегруз судна, в трюме демонтированы герметичные переборки для большего вмещения рыбы, погибло 69 человек.

Теплоход «Москва-130», «Татнефть», 2016 год, перегруз судна, вместимостью на 300 пассажиров, шел из п. Студенец, имея на борту 440 пассажиров, к счастью, никто не погиб, по заявлению пассажиров возбуждено уголовное дело. Случай указывает на обыденность перегруза судов.

Ту-154, 2006 год, под Донецком на Украине, экономия топлива, при попытке пройти грозу на большей высоте, сорвался в плоский штопор, погибло 160 человек.

Боинг-737, 2016 год, Ростов-на-Дону, экономия топлива, отказался уйти на аэродром Краснодара из-за штормовой погоды в Ростове, при посадке в Ростове экипаж не справился с управлением, погибло 69 человек.

I. ВЗАИМОДЕЙСТВИЕ ДВИЖУЩЕЙ СИЛЫ С ТЕЛОМ, УВЛЕКАЕМЫМ ЕЮ В ДВИЖЕНИЕ

Предисловие

В литературе [1] и [2] впервые, на основе первичных законов физики, приведен вывод формулы скорости хода грузовых судов водного транспорта [1], и крейсерской скорости полета воздушных судов гражданской авиации [2].

Там же раскрыта причина низкой, на грани убыточности, рентабельности указанной транспортной техники и предложен способ ее кратного повышения.

Проверка истинности, практической достоверности формул осуществлялась на четырех действующих грузовых судах водного транспорта водоизмещением от 1636 м³ («Беломорский») до 6755 м³ («Волго-Дон») [1], и на четырех действующих авиалайнерах со взлетной массой от 161,6 т (Ил-62) до 560 т (аэробус А380).

Проверка заключалась в сравнении фактической, паспортной скорости указанной транспортной техники со скоростью этих же судов, рассчитанной по физическим формулам скорости при исходных, паспортным техническим характеристикам. Расчеты представлялись в табличной форме.

Слабым местом в работе является нечеткость и размытость описания взаимодействия движителей с увлекаемой ими техникой, гребного винта с корпусом судна водного транспорта и реактивного двигателя с корпусом авиалайнера.

Слабое место в [1] и [2] является основанием недоверию у специалистов, ни к самим формулам, ни к запатентованному способу кратного увеличения рентабельности транспортной техники [5], при той же мощности двигателей. Это служит основанием препятствию практической реализации изобретения на судах Минморречфлота и Росавиации.

Принцип взаимодействия движителя и буксируемого тела в настоящей работе рассмотрен применительно к простейшему случаю буксировки тела наземным транспортом, это помогло раскрыть работу гребного винта при буксировке судна в воде.

На рис.1 простейшее цилиндрическое тело 1 массой M, длиной l и площадью поперечного сечения ω, погружено на буксировочную тележку 2, приводимую в движение мощностью двигателя автомобиля, передаваемой к заднему приводу вращения его ведущих колес.

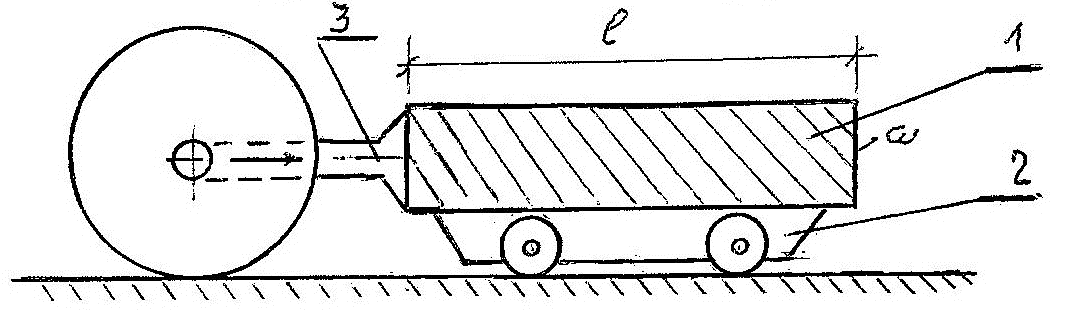
Рис. 1. Тело, помещенное на тележку

1. ДВА ТИПА ДВИЖУЩИХ СИЛ

По характеру действия движущие силы разделяются на два типа – силы статические и силы ударно-дискретные.

Силы статические – это силы, когда упором движителю служит сама Земля: силы от всевозможных тяг (конных, автотяг и т.п.).

Примером статической движущей силы является сила от тяги буксировочной тележки при буксировке модели судна в опытовом бассейне.

Силы ударно-дискретные – это силы, когда упором движителю служит не Земля, а реакция отбрасываемой движителем жидкости. Силы ударно-дискретные возникают между массами, одной из которых является масса m движителя, а другой – масса M судна.

Примером ударно-дискретной является сила, создаваемая гребным винтом при буксировке реального судна.

В общем виде ударно-дискретные движущие силы создаются гидроаэродвижителями – это гребные винты и центробежные насосы, для движения в воде; воздушные винты и реактивные двигатели, для движения в воздухе.

2. СТАТИЧЕСКИЙ ХАРАКТЕР ДЕЙСТВИЯ ДВИЖУЩЕЙ СИЛЫ

Первый закон Ньютона, закон инерции гласит, что тело в состоянии покоя обладает состоянием покоя до тех пор, пока внешнее воздействие не заставит изменить это состояние.

Все тела состоят из молекул, плотно касающихся между собой электронными оболочками, поэтому момент приложения к телу силы распространяется по нему со скоростью электромагнитной волны, со скоростью света. Следовательно, момент приложения движущей силы F, момент начала давления бампера автомобиля (рис. 1) на тыловую грань тела ощущается мгновенно всеми молекулами тела.

С момента приложения силы к телу, в нем одновременно мгновенно начинает действовать на каждую молекулу равная и противоположно направленная сила инерции покоя.

Под действием равных и противоположно направленных сил, силы движущей и силы инерции покоя, каждая молекула в объеме тела сжимается, уменьшая свой линейный размер.

В результате действия движущей силы, деформации сжатия отдельных молекул суммируются в величине Δl линейной деформации всего тела (рис. 2б).

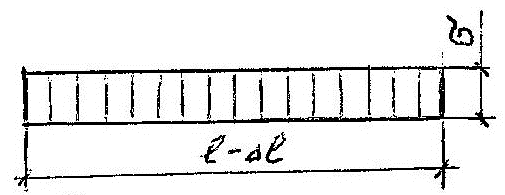
а)

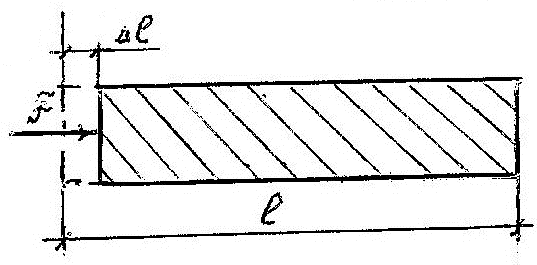
б)

Рис. 2. Эпюра напряжений $\sigma$ статического сжатия

Согласно закону инерции, тело сохраняет состояние покоя, пока не станет полностью охвачено воздействием силы F, то есть не окажется полностью сжатым на величину деформации сжатия, Δl (рис.2б).

Время T полного сжатия тела движущей силой F равно

\(T=\frac{l}{c}\);     (1.1)

где c – скорость волны сжатия по телу, скорость распространения по телу звуковой волны.

Время T по (1.1) является временем оседлости тела и означает, что любое тело, обладающее массой, невозможно вывести из состояния покоя быстрее, чем время его оседлости, как бы ни велика была действующая на него сила.

Для того чтобы вывести тело из состояния покоя, в нем необходимо создать запас потенциальной энергии его упругой деформации, высвобождение которой переходит в работу по выведению тела из состояния покоя.

Скорость нарастания деформации сжатия, скорость суммирования деформаций отдельных молекул, имеет вид

\(\Delta\upsilon=GT\);    (1.2)

G – ускорение тела движущей силой F, по второму закону Ньютона равно

\(G=\frac{F}{M}\);    (1.3)

M – масса тела, равна:

\(M=\rho\omega l\);    (1.4)

Суммарная деформация сжатия тела Δl, при постоянной скорости ее нарастания (1.2), за время оседлости тела T по (1.1), составляет

\(\Delta l=\Delta\upsilon T=GT^2\);    (1.5)

Вид формулы скорости $\Delta\upsilon$ по (1.2) подтвержден практикой и закреплен в науке законом Гука.

Действительно, подставляя в выражение (1.5) ускорение по (1.3), а время оседлости T по (1.1), имеем

\(\Delta l=\frac{F}{M}\frac{l^2}{c^2}\);    (1.6)

Раскрывая в (1.6) массу M по (1.4), выражение деформации принимает вид

\(\Delta l=\frac{F}{\rho\omega l}\frac{l^2}{c^2}\);    (1.7)

Сокращая числитель и знаменатель (1.7) на длину, и учитывая, что отношение силы к площади есть напряжение

\(\sigma=\frac{F}{\omega}\);    (1.8)

а произведение плотности на квадрат скорости звука, есть модуль упругости Юнга

\(E=\rho c^2\);    (1.9)

Выражение деформации Δl принимает окончательный вид

\(\Delta l=\frac{\sigma l}{E}\);    (1.10)

Разделив (1.10) на длину l, получаем формулу закона Гука

\(\frac{\Delta l}{l}=\frac{\sigma}{E}\);    (1.11)

Давление в фронте волны сжатия выражается формулой

\(Pсж=ρΔυc\);    (1.12)

Подставляя в (1.12) $\Delta\upsilon$ по (1.2) и раскрывая в ней ускорение по (1.3), а массу по (1.4), после сокращений, с учетом (1.8), получаем давление $Pсж$ в виде

\(Pсж=σ=ρΔυc\);    (1.13)

После достижения волной сжатия передней носовой грани тела, оно оказывается полностью в сжатом состоянии, а скорость $\Delta\upsilon$ его упругого сжатия переходит в скорость равномерного движения самого тела. Но по первому закону Ньютона, тело не может находиться в состоянии равномерного движения, так как на него продолжает действовать движущая сила F, выводя его из этого состояния.

Поэтому в этот момент перехода, в теле мгновенно вновь возникает сила инерции равномерного движения, а движущиеся равномерно все его молекулы получают дополнительно ускорение G. В результате, за время T нахождения тела в состоянии равномерного движения, скорость его поступательного движения возрастает вдвое. Тело перешло в ускоренное движение, и в общем виде скорость ускоренного движения тела за время t выражается формулой

\(\upsilon=n_0\Delta\upsilon\);    (1.14)

где n₀ – разгонное число, выражает, сколько раз тело движущей силой выводилось из состояния равномерного движения, преодолевая действие силы инерции равномерного движения, равно

\(n_0=\frac{t}{T}\);    (1.15)

где t – время разгона тела движущей силой из состояния покоя в состояние равномерного движения.

Из вышесказанного следует вывод:

При движении тела движущей силой, упором для которой является Земля, тело все время, всегда, находится в сжатом состоянии, а напряжения сжатия  являются скалярной величиной с эпюрой на рис. 2а.

Постоянное сжатие тела обеспечивается на участке ускоренного движения силой движущей и, равной ей, силой инерции покоя, а на участке равномерного движения – силой движущей и, равной ей, силой сопротивления среды, окружающей тело, (трение, лобовое сопротивление).

3. ПОТЕНЦИАЛЬНАЯ И КОНСЕРВАТИВНАЯ ЭНЕРГИЯ УПРУГО СЖАТОГО ТЕЛА

К моменту полного сжатия тела под действием равных и противоположно направленных сил, силы движущей и силы инерции покоя (рис. 2б) над телом совершена работа по его сжатию, равная

\(A=F\Delta l\);    (1.16)

Работу выразим в виде энергии, сосредоточенной в теле к концу его полного сжатия.

Силу F представим как произведение напряжений $\sigma$ (1.13) на площадь поперечного сечения тела

\(F=\rho\Delta\upsilon c\omega\);    (1.17)

Подставляя в (1.16) F по (1.17), а деформацию Δl по (1.5), получаем выражение внутренней энергии вида

\(Э=ρΔυcωΔυT\);    (1.18)

С учетом T по (1.1) и массы тела M по (1.4), после сокращений и преобразований, выражение полной внутренней энергии, сосредоточенной в нем к моменту полного сжатия, приводится к окончательному виду

\(Э=MΔυ^{2}\);    (1.19)

Потенциальная энергия, заключенная в упруго сжатом теле, согласно закону физики [3, §45, с.179] выражается формулой

\(U=\frac{1}{2}E\varepsilon^2V\);    (1.20)

где E – модуль упругости тела по (1.9);

ε – относительная деформация тела, имеет вид

\(\varepsilon=\frac{\Delta l}{l}\);    (1.21)

V – объем тела, равный

\(V=\omega l\);    (1.22)

Подставляя в (1.20) E по (1.9), ε по (1.21), а в ней Δl по (1.5) и T по (1.1), затем V по (1.22), окончательный вид формула (1.20) примет выражение

\(U=\frac{1}{2}\rho c^2\frac{\Delta\upsilon^2l^2}{l^2c^2}\omega l\);    (1.23)

Окончательно формула потенциальной энергии, заключенной в сжатом теле, учитывая, что масса тела есть $M=\rho\omega l$, после сокращений в (1.23), приводится к виду

\(U=\frac{1}{2}M\Delta\upsilon^2\);    (1.24)

Из сравнения (1.19) и (1.24) следует вывод.

Для выведения тела из состояния покоя, за время его оседлости T, надо затратить в два раза большую энергию, чем полученное им за это время приращение кинетической энергии поступательного движения.

Разница между полной энергией упругого сжатия (1.19) и потенциальной энергией (1.24) является внутренней консервативной энергией, которая совершать полезную работу не может. При ускоренном разгоне тела из состояния покоя до скорости равномерного движения, находящегося в постоянно сжатом состоянии, эта энергия представляет энергию теплового колебания ядер молекул, слагающих тело, относительно центра их равновесного положения в молекулах.

4. УДАРНО-ДИСКРЕТНЫЙ ХАРАКТЕР ДЕЙСТВИЯ ДВИЖУЩЕЙ СИЛЫ

Из первого закона Ньютона, закона инерции следует, что все тела, обладающие массой, обладают и временем оседлости, в течение которого они сохраняют состояние покоя и не могут быть выведены из этого состояния за меньшее время, чем время оседлости, как бы ни велика была действующая сила.

На примере движения судна (рис.3) описан принцип взаимодействия движителя, гребного винта, массой m_гр, с корпусом судна 3, массой M.

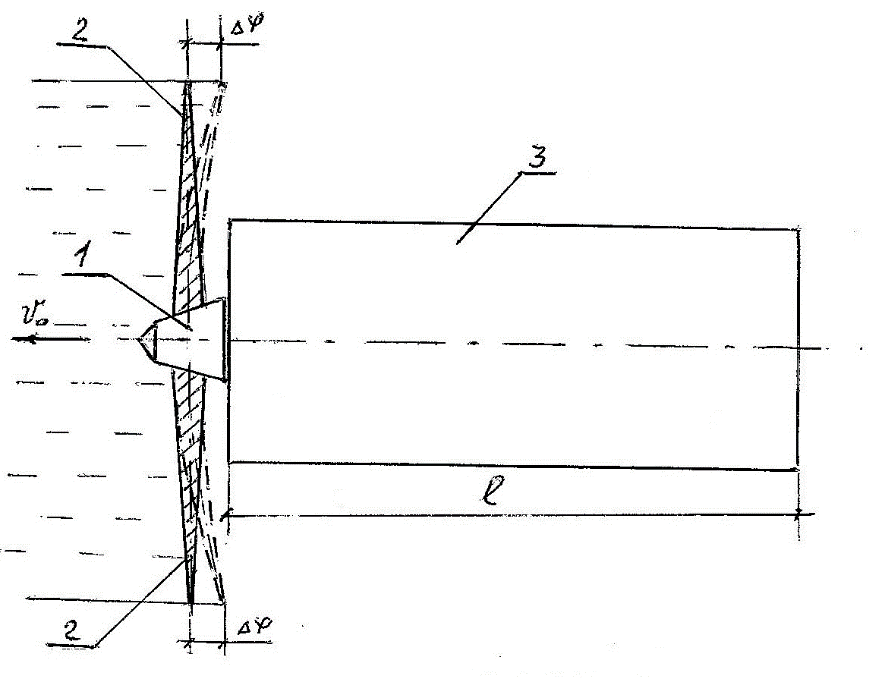
Рис. 3. Деформация прогиба лопастей гребного винта

Обладая состоянием покоя, гребной винт с расчетным числом оборотов его лопастей 2, разгоняет струю жидкости до скорости $\upsilon_0$ (рис.3), сила динамического давления которой F передается на лопасти, как реакция на отбрасываемую жидкость, по величине равная и противоположно направленная силе F динамического давления струи.

По существу, сила F для корпуса судна является движущей силой.

Обладая массой, гребной винт сохраняет состояние покоя, находясь под действием двух равных и противоположно направленных сил, – силой движущей F и равной ей силой инерции покоя винта.

Под действием указанных сил в гребном винте накапливается потенциальная энергия упругого прогиба лопастей винта относительно ступицы 1.

При деформации прогиба лопастей $\Delta\phi$ (рис.3), достигшей своей величины, соответствующей величине силы F, сила инерции покоя гребного винта мгновенно обращается в нуль, а накопленная потенциальная энергия прогиба лопастей, так же мгновенно, высвобождается, приводя положение лопастей винта в нейтральное, ненагруженное положение.

Гребной винт под действием высвободившейся потенциальной энергии срывается из состояния покоя с ускорением G_гр, равном

\(G_{гр}=\frac{F}{m_{гр}}\);    (1.25)

где F – движущая сила, кН;

m_гр – масса гребного винта, т;

G_гр – ускорение винта, м/с².

В момент удара ступицы винта по корпусу судна, по 3-су закону Ньютона, гребной винт испытывает со стороны корпуса торможение G_трм. против ускорения гребного винта, равное

\(Gтрм.=Gгр-G\);    (1.26)

где G – ускорение судна движущей силой F по (1.3).

К концу времени оседлости судна T по (1.1), времени передачи ему энергии удара гребного винта, скорость $\upsilon_{гр}$ набегания гребного винта на судно падает до значения

\(\upsilon_{гр}=(G_{гр}-G_{трм.})T\);    (1.27)

Раскрывая в (1.27) G_трм. по (1.26), получаем выражение скорости гребного винта в виде

\(\upsilon_{гр}=(G_{гр}-G_{гр}+G)T\);    (1.28)

Сокращения в (1.28) приводят к тому, что к концу времени T оседлости судна, времени передачи энергии удара от винта судну, скорость набегания гребного винта падает до приращения скорости хода судна, то есть

\(υ_{гр}=Δυ\);    (1.29)

Гребной винт и судно в этот момент времени движутся как единое целое, когда давление между ними равно нулю.

За время T торможения гребного винта в нем, при непрерывном вращении лопастей винта с расчетным числом оборотов, вновь оказывается накоплена потенциальная энергия лопастей за счет их перемещения из нейтрального положения в положение нагруженного состояния с деформацией прогиба $Δϕ$ как на рис.3.

Время T передачи силы удара ступицей от гребного винта судну, как движущей силы, одновременно является и временем накопления в нем потенциальной энергии прогиба лопастей.

Гребной винт одновременно передает энергию удара корпусу судна и, в то же время, испытывает прогиб лопастей, при постоянном их вращении, из-за реакции торможения гребного винта при набегании на судно.

Процесс передачи энергии от движителя, гребного винта, судну непрерывный, когда конец передачи энергии одного удара является началом передачи энергии следующего удара, за счет потенциальной энергии прогиба лопастей винта, накопленной в нем за время импульса предыдущего удара.

Характерным и существенным отличием ударного приложения движущей силы является векторность напряжений, возникающих от нее в корпусе судна. Эпюра напряжений к моменту завершения передачи энергии каждого удара судну за время T его оседлости имеет треугольный вид (рис.4а).

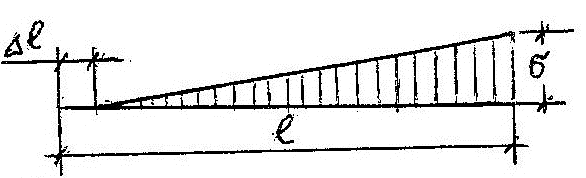
а)

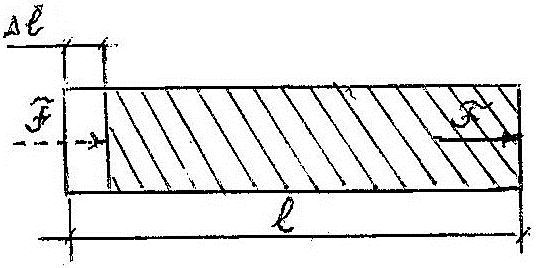
б)

Рис. 4. Эпюра ударных напряжений

При статическом характере движущей силы, когда упором движителю является сама Земля (рис.2), эта сила постоянно приложена к тыльной грани тела, а буксируемое силой тело постоянно находится в сжатом состоянии.

При ударном характере движущей силы (рис.4), когда упором движителю служит реакция отбрасываемой им жидкости, плоскость приложения движущей силы в виде силы ударного давления в фронте ударной волны F_уд., равной

\(F=ρΔυcω=F_{уд.}\);    (1.30)

является подвижной, перемещающейся по судну со скоростью звука от тыльной его грани до носовой грани.

В момент достижения движущей силой F (1.30) носовой грани судна (рис.4б) потенциальная энергия сжатия в нем мгновенно высвобождается, осуществляя удар носовой гранью по встречной жидкости. При этом положение носовой грани мгновенно смещается на величину Δl упругого сжатия судна, восстанавливая длину l судна.

В результате энергия очередного удара гребного винта передается судну по абсолютно несжатому его состоянию.

Частота $\nu_{0}$ ударного приложения движущей силы обратна времени T оседлости судна

\(\nu_{0}=\frac{1}{T}\);    (1.31)

Частота $\nu_{0}$ является и частотой периодического полного сжатия судна на величину деформации Δl по (1.5) движущей силой, а также, и частотой ударов носовой поверхностью по встречной жидкости.

На каждое полное периодическое сжатие судна затрачивается в 2 раза большая энергия (1.19), чем приращение кинетической энергии за это же время T сжатого судна.

Поэтому за время t движения судна, при разгонном числе n₀ по (1.15), полная энергия, затраченная на ускоренное движение сжатого судна, равна

\(E_{сж.}=n_0(\frac{MΔυ^2}{2})\);    (1.32)

При ударном приложении судну этой же силы, при периодически полном его сжатии, затрачивается в 2 раза большая энергия

\(E_{уд.}=n_0 (MΔυ^2)\);    (1.33)

Вывод: используя при движении в жидкостях, вода и воздух, в качестве упора реакцию отбрасываемой жидкости, гребным винтом в воде, и реактивным двигателем – в воздухе, на движение затрачивается в два раза большая энергия, чем для движителя, использующего в качестве упора Землю.

II. ПРИЧИНЫ И ПОСЛЕДСТВИЯ ДВОЙНОГО ЗАНИЖЕНИЯ ДВИЖУЩЕЙ СИЛЫ

Современная экспериментальна (эмпирическая) гидроаэродинамика учитывает перерасход энергии при движении в жидкостях, вода и воздух, введением КПД движителя равного 0.5, указывающего, что 50% из всего топлива, расходуемого на движение, тратится бесполезно из-за несовершенства движителей, гребного винта у судов водного транспорта и реактивного двигателя – у воздушных судов. Характерно, что у совершенно разных движителей КПД одинаковый.

По гребному винту в [3] говорится: «КПД гребного винта колеблется в пределах 50-70%. КПД равный 70% считается очень высоким. Обычно такой КПД бывает у малооборотных гребных винтов большого диаметра. Для высокооборотных винтов малого диаметра КПД редко бывает выше 60% (как правило, около 50%)».

По реактивному двигателю в [4] сказано: «КПД реактивного двигателя достигает 47-60%, в среднем 50%».

Известно, что мощность движителя есть произведение движущей силы на скорость точки ее приложения, скорость движителя.

Введением КПД движителя, равным 0.5, экспериментальная гидроаэродинамика фактически в 2 раза уменьшает движущую силу.

Действительно, измеряя упоромером движущую силу в месте ее приложения на упорном подшипнике в корпусе судна, ее величина, равная тяге движителя в момент ее приложения, к концу времени T оседлости, смещается на носовую грань, а в месте приложения – становится равной нулю. Из-за инерционности упоромера, он фиксирует движущую силу по величине, равную среднему значению между нулем и величиной тяги движителя, т.е.

\(F≠\frac{1}{2}T_c\);    (2.1)

На самом деле, движущей силой является тяга движителя, только ее место приложения к корпусу смещается в виде ударной волны со скоростью звука от места измерения к фронтальной грани тела (рис.4б), то есть

\(F=T_c\);    (2.2)

2.1. ЗАНИЖЕНИЕ ПРОЧНОСТИ КОРПУСА

Исторически укоренившейся ошибкой экспериментальной гидроаэродинамики является приложение движущей силы, как реакции отбрасываемой жидкости, непосредственно к корпусу буксируемого судна, а не к движителю.

Этим неоправданно принимается положение, что движителю в качестве упора служит сама Земля, а судно в движении находится в статически сжатом состоянии этой силой.

На самом деле, в действительности корпус судна находится под действием в 2 раза большей силы, но характер воздействия ее на корпус является не статическим, а ударным.

Этим в два раза занижается продольная нагрузка, действующая сжимающе на корпус судна, и не учитывается усталость металла корпуса при ударном действии нагрузки. Это должно ограничивать срок службы судов в связи со снижением со временем предела прочности корпуса из-за усталости металла.

III. МЕРОПРИЯТИЯ КРАТНОГО ПОВЫШЕНИЯ КПД РЕАКТИВНЫХ ДВИЖИТЕЛЕЙ

Причиной двойного перерасхода энергии реактивными движителями, гребным винтом и реактивным двигателем, использующими в качестве упора реакцию отбрасываемой жидкости, является ударно-дискретный характер движителя движущей силы.

Для повышения эффективности движителей, надо не допускать, исключить возможность ударного приложения движущей силы от движителя буксируемому судну.

Известны способы снижения, демпфирования ударных нагрузок на сухопутном транспорте, начиная от надувных шин колес автотранспорта и металлических рессор между кузовом и колесными парами, и кончая буферами с обеих сторон локомотивов и вагонов железнодорожного транспорта.

Предлагается для полного демпфирования, полного исключения ударной передачи движущей силы от гребного винта корпусу судна, разместить между носовой частью судна и цилиндрической частью упругую вставку из отдельных стальных, как и корпус судна, стержней (рис.5).

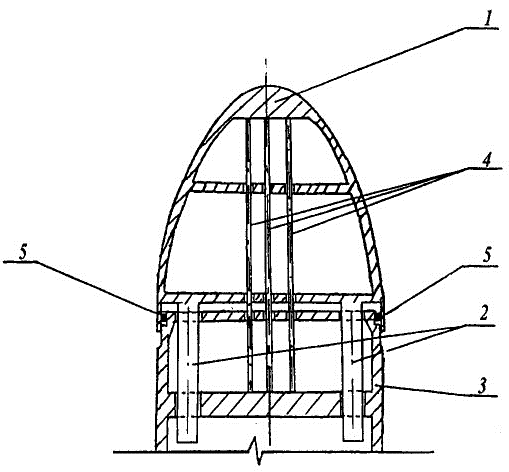
Рис. 5

Носовую часть корпуса 1 отделяют от его цилиндрической части 3 и удерживают у сечения раздела на направляющих консолях 2, воспринимающих поперечные усилия в корпусе, действующие в плоскости раздела между носовой и цилиндрической частями.

Носовую часть соединяют с цилиндрической стержнями 4 из металла, воспринимающими продольную силу, величина которой определена движущей силой (2.2), то есть тягой движителя.

Примыкание носовой части корпуса к цилиндрической выполняют продольно подвижным и герметичным с устройством сальника 5.

Для исключения возможности ударной передачи движущей силы от движителя буксируемому судну, в корпус судна помещена упругая вставка, роль которой выполняют стержни 4 (рис.5).

Цель упругой вставки, уменьшить жесткость k корпуса судна, увеличить его податливость сжатию от действия сжимающей его силы, движущей силы.

Из закона Гука жесткость корпуса судна выражается формулой

\(k=\frac{Eω}{l}\);    (3.1)

Подставляя в (3.1) модуль Юнга по (1.9) и умножая числитель и знаменатель на длину l корпуса, получаем выражение

\(k=\frac{ρc^2 ωl}{l^2}\);     (3.2)

Учитывая, что в (3.2) $ρωl=M$ по (1.4), а $\frac{l}{c}=T$ по (1.1), выражение жесткости корпуса по (3.1) преобразуется в формулу

\(k=\frac{M}{T^2} \);    (3.3)

Из (3.3) следует, что для уменьшения жесткости корпуса судна необходимо увеличить время T его оседлости, а из формулы (1.1) видно, что для увеличения времени T оседлости, надо уменьшить скорость c звука по корпусу судна. Из [1, §8, (8.1)] следует, что наиболее эффективной скоростью звука, при которой нейтрализуется лобовое (волновое) сопротивление, является ее величина, равная

\(c_{эф}=\frac{a}{2}\);    (3.4)

где a – скорость звука по встречной жидкости, для воды равна 1435 м/с, для воздуха – 300 м/с на высоте полета 10000 м.

Формула (3.4) подтверждена практикой движения обитателей водной среды, дельфинов [1, (8.6)], у которых скорость звука по их телу равна 707 м/с, практически в 2 раза меньше скорости звука в воде, что согласуется с (3.4).

Из закона Гука суммарная жесткость упругой вставки из $n_{ст}$ стержней длиной $l_{ст}$ и модуля Юнга для стали $E_{ст}$ выражается формулой

\(k_{ст}=\frac{E_{ст} A}{l_{ст}} \);    (3.5)

где A_ст – суммарная площадь поперечного сечения  стальных стержней

\(A=\frac{n_{ст} πd^2}{4}\);    (3.6)

Эффективная жесткость корпуса, следуя (3.3), равна

\(k_{эф}=\frac{M}{T_{эф}^{2}}\);    (3.7)

где T_эф – эффективное время оседлости судна;

\(T_{эф}=\frac{l}{c_{эф}}\);    (3.8)

Приравнивая (3.5) и (3.7), определяется диаметр стержней упругой вставки по формуле

\(d=\sqrt{\frac{4l_{ст}M}{E_{ст}T_{эф}^{2}\pi
n_{ст}}}\);    (3.9)

Отношение (3.3) к (3.7) показывает, во сколько раз надо уменьшить жесткость корпуса судна при его движении в воде в связи с тем, что скорость звука по стальному корпусу 5100 м/с снижается до половины значения скорости звука в воде 1435/2 м/с. Это отношение после сокращений приводится к виду

\(\frac{k}{k_{??}}=\frac{4c^{2}}{a^{2}}=\frac{4\cdot 
5100^{2}}{1435^{2}}=50.5\)раз;    (3.10)

Формула скорости хода судов водного транспорта и крейсерской скорости полета авиалайнеров, то есть для реактивных движителей, по [1, §5, (5.10)], по форме имеет общий, один и тот же вид

\(\upsilon =\sqrt{\frac{N}{M}n_{0}T}\);    (3.11)

При равной буксировочной мощности N и равных прочих показателях в формуле, только за счет увеличения времени оседлости судна с T по (1.1) до T_эф по (3.8), скорость хода судна увеличивается в $\upsilon _{эф}/\upsilon$ раза, равное

\(\frac{\upsilon _{эф}}{\upsilon 
}=\sqrt{\frac{T_{эф}}{T}}=\sqrt{\frac{2c}{a}}=2.67\)раз;    (3.12)

Для воздушного судна, Ил-96-300, учитывая для него скорость звука по корпусу [2, т.1 п.21] c=1071.43 м/с и скорость звука по воздуху a=300 м/с, это соотношение принимает величину

\(\frac{\upsilon _{эф}}{\upsilon }=\sqrt{\frac{2\cdot 
1071.43}{300}}=2.67\)раз;    (3.13)

Вывод: у реактивных движителей при оборудовании их устройствами, снижающими упругость, жесткость корпуса в 50.5 раз (3.10), рентабельность транспортируемых судов повышается пропорционально квадрату увеличения скорости движения, то есть в 7.1 раза.

Объясняется это тем, что в момент ударного приложения ступицей гребного винта движущей силы к корпусу судна, в работу мгновенно включается упругая вставка, от начала стержней которой в них возникает не ударная волна, а волна сжатия, напряжения от которой в стержнях являются скалярной величиной вида (рис.2а).

Далее процесс передачи энергии от гребного винта корпусу судна развивается по схеме статического приложения движущей силы, когда судно на разгонном участке движения находится постоянно в сжатом состоянии при деформации упругой вставки Δl, равной

\(\Delta l=GT_{эф}^{2}\);    (3.14)

IV. ПРИМЕРЫ РАСЧЕТА ГИДРОАЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ДЕЙСТВУЮЩЕГО ТРАНСПОРТА

4.1. СУХОГРУЗ ВОЛГО-ДОН

Следуя [1, т.2], сухогруз Волго-Дон водоизмещением V=6755 м³, то есть массой M=6755 т и установленной мощностью двигателей N_уст=2000 л.с.=1472 кВт, приводится в движение двумя гребными винтами диаметром 1.8 м и общей их массой $m_{гр}=2\times 706=1.412m$. Сухогруз разгоняется до скорости хода равномерного движения $\upsilon =21.0км/ч=5.83м/с$.

1. Буксировочная мощность N судна в формуле скорости (3.10) равна

\(N=\eta\cdot N_{уст}=0.9⋅1472=1324.8кВт\);    (4.1)

где $\eta =0.90$ – КПД силовой установки судна, учитывающий потери энергии в валопроводе и редукторе;

2. Движущая сила, тяга двигателей

\(F=\frac{N}{\upsilon }=\frac{1324.8}{5.83}=227.24\)кН;    (4.2)

3. Ускорение, испытываемое гребными винтами при выведении их из состояния покоя (1.25)

\(G_{гр}=\frac{F}{m_{гр}}=\frac{227.24}{1.412}=160.9м/с^{2}\);    (4.3)

4. Время оседлости сухогруза, [1, т.2, п.14], равно

T=0.023с;    (4.4)

5. Разгонное число [1, т.2, п.16] равно

\(n_{0}\)=7504;    (4.5)

6. Скорость хода сухогруза по (3.11) равна

\(\upsilon 
=\sqrt{\frac{N}{M}n_{0}T}=\sqrt{\frac{1324.8}{6755}7504\cdot 
0.023}=5.82\)м/с;    (4.6)

Скорость хода, рассчитанная по физической формуле, совпала по величине с фактической скоростью хода сухогруза $\upsilon =5.83$м/с.

7. Эффективное время оседлости судна по (3.8)

\(T_{эф}=\frac{l_{ц}}{c_{эф}}=\frac{117}{717.5}\approx 0.163\)с;    (4.7)

где l_ц=117м – длина сухогруза, приведенная к длине цилиндрического тела с постоянной площадью поперечного сечения [1, т.2, п.13];

\(c_{эф}=\frac{c}{2}=\frac{1435}{2}\) – эффективная скорость звука по корпусу сухогруза, равна половине скорости звука во встречной жидкости, воде.

8. Эффективная скорость хода сухогруза после уменьшения жесткости корпуса посредством упругой вставки, определяется простой заменой в формуле (4.6) времени оседлости T по (4.4) на эффективное время T_эф по (4.7), равна

\(\upsilon =\sqrt{\frac{1324.8}{6755}7504\cdot 
0.163}=15.5м/с(55.8км/ч)\);    (4.8)

Скорость хода сухогруза 21.0 км/ч увеличилась при той же мощности двигателей до эффективной скорости 55.8 км/ч, то есть в 2.67 раза.

9. Диаметр стержней из Ст.3 в упругой вставке определяется по (3.9)

\(d=\sqrt{\frac{4l_{cm}M}{E_{cm}T_{эф}^{2}\pi 
n_{cm}}}=\sqrt{\frac{4\cdot 10\cdot 6755\cdot 10^{3}}{2.04\cdot 
10^{11}\cdot 0.163^{2}\cdot 3.14\cdot 10}}=40\)мм;    (4.9)

где $l_{cm}$ =10 м – длина стержней в упругой вставке;

$E_{cm}$ =2.04·10⁵ Мпа – модуль упругости Ст.3;

 $n_{cm}$=10 шт. – число стальных, Ст.3, стержней вставки.

10. Напряжения упругого сжатия стержней вставки:

\(\sigma =\frac{F}{A}=\frac{4F}{\pi 
d^{2}n_{cm}}=\frac{4\cdot 227.24\cdot 10^{3}}{3.14\cdot 0.04^{2}\cdot 
10}=18.1\)МПа(184.5кгс/см²);    (4.10)

где A – суммарная площадь сечения стержней.

Прочность стержней на сжатие обеспечена, так как напряжения σ=184.5кгс/см² значительно меньше допускаемых напряжений на сжатие R_y=1500÷1700кгс/см².

4.2. АВИАЛАЙНЕР ИЛ-96-300

1. Рабочий орган движителя.

У судов водного транспорта рабочим органом, выводящим из состояния покоя движитель, гребной винт, являются лопасти гребного винта.

У авиалайнеров рабочим органом, выводящим из состояния покоя движитель, реактивный двигатель, является камера сгорания.

Реактивный двигатель, обладая массой, мерой инертности, обладает и временем оседлости до тех пор, пока в стенках камеры сгорания, под действием давления газа от сгораемого в ней топлива, накопится потенциальная энергия их упругого растяжения, а стенки камеры, при увеличении ее объема отойдут по всему периметру от положения ненагруженного состояния на расстояние Δϕ.

При предельном расширении объема камеры на Δϕ, соответствующем силе F динамического давления струи газа, истекающей из сопла, сила инерции покоя двигателя мгновенно обращается в нуль, а накопленная потенциальная энергия растяжения стенок камеры, так же мгновенно высвобождается, приводя стенки камеры сгорания в ненагруженное, нейтральное положение.

Двигатель под действием высвободившейся потенциальной энергии срывается из состояния покоя с ускорением G_дв по (1.25), осуществляя удар по корпусу воздушного судна.

Далее процесс передачи энергии от реактивного двигателя воздушному судну развивается по описанной схеме передачи энергии от гребного винта.

При постоянной подаче расхода топлива в камеру сгорания, реактивный двигатель одновременно передает энергию удара воздушному судну и, в то же время накапливает энергию упругого растяжения в стенках камеры, приводя их из ненагруженного положения в нагруженное положение  для следующего удара по корпусу.

2. Буксировочная мощность N воздушного судна.

Авиалайнер Ил-96-300, взлетной массой M=250 т, разгоняется 4-мя двигателями ПС-90А общей тягой T_c=64 тс (627.84 кН) до крейсерской скорости полета с максимальной нагрузкой $\upsilon=$241.67м/с(870км/ч). Суммарная масса двигателей равна m_дв=4×4.16=16.64m.

Тяга двигателя, являясь для него движущей силой F по (2.2), при скорости полета $\upsilon$, определяет мощность двигателя, равную

\(N=F\upsilon =627.84\cdot 241.67=1.52\cdot 10^{5}\)кВm;    (4.11)

3. Ускорение, испытываемое двигателями при срыве их из состояния покоя и ударе по опорной плите корпуса воздушного судна по (1.25), равно

\(G_{дв}=\frac{F}{m_{дв}}=\frac{627.84}{16.64}=37.73\)м/с²;    (4.12)

4. Разгонное число авиалайнера по [2, т.1, п.25] определилось равным

\(n_{0}\)=2192;     (4.13)

5. Время оседлости воздушного судна [2, т.1, п.22] равно

T=0.0439с;    (4.14)

6. Скорость полета Ил-96-300 формулой (3.11) определяется равной

\(\upsilon 
=\sqrt{\frac{N}{M}n_{0}T}=\sqrt{\frac{1.52\cdot 10^{5}}{250}2192\cdot 
0.0439}=\)241.88м/с(870.8км/ч);    (4.15)

Скорость полета Ил-96-300, рассчитанная по физической формуле скорости, практически совпала с фактической скоростью (870 км/ч) авиалайнера.

7. Эффективное время оседлости Ил-96-300 по (3.8) [2, т.2, п.11]

\(T_{эф}=\frac{l_{ц}}{c_{эф}}=\frac{47.04}{150}=0.3136\)с;     (4.16)

где l_ц =47,04 м – длина авиалайнера, приведенная к длине цилиндрического тела [2, т.1, п.16];

\(c_{эф}=\frac{c}{2}=\frac{300}{2}\) – эффективная скорость звука по корпусу авиалайнера, равна половине скорости звука по воздуху на высоте полета 10000 м.

8. Эффективная скорость полета Ил-96-300, после уменьшения жесткости, упругости его корпуса посредством упругой вставки, определяется заменой в формуле (4.15) времени оседлости по (4.14) на эффективное время по (4.16)

\(\upsilon _{??}=\sqrt{\frac{1.52\cdot 
10^{5}}{250}2192\cdot 0.3136}=\)646.49м/с(2327.4км/ч);    (4.17)

Уменьшение упругости корпуса Ил-96-300, при той же мощности двигателей, приводит к увеличению скорости полета в 2.67 раза, до сверхзвуковой скорости $\upsilon =2.15$ Маха.

9. Диаметр стержня упругой вставки.

Из всех материалов по модулю Юнга, для использования в качестве упругой вставки для воздушных судов, наиболее подходит оргстекло с модулем упругости $E_{орг.}=3\cdot 10^{3}$МПа [2, рис.9].

Диаметр стержня упругой вставки из оргстекла, при длине стержня 13.2 м по формуле (3.9) определяется равным

\(d=\sqrt{\frac{4l_{орг.}M}{E_{орг.}T_{эф}^{2}\pi 
}}=\sqrt{\frac{4\cdot 13.2\cdot 250\cdot 10^{3}}{3\cdot 10^{9}\cdot 
0.3136^{2}\cdot 3.14}}=119.34\)мм;    (4.18)

10. Напряжение сжатия в стержне равны

\(\sigma =\frac{F}{A}=\frac{4F}{\pi 
d_{орг.}^{2}}=\frac{4\cdot 627.84\cdot 10^{3}}{3.14\cdot 
0.11934^{2}}=\)56.13МПа(572.17кгс/см²);    (4.19)

Допустимое напряжение сжатия оргстекла R_у=70МПа(713.6кгс/см²).

Прочность стержня на сжатие обеспечена, так как

$$\sigma =56.13МПа<R_{y}=70МПа$$

ВЫВОДЫ

1. Низкая, на грани убыточности рентабельность судов водного транспорта и воздушных судов объясняется общей причиной – использованием движителями в качестве упора реакцию отбрасываемой жидкости, а не Землю, подобно движителям наземного сухопутного транспорта. Особым отличием реактивных движителей, гребного винта и реактивного двигателя, является ударный характер действия развиваемой ими движущей силы, на которую затрачивается в 2 раза большая энергия, чем на такую же силу от движителей наземного транспорта.
2. Способом повышения рентабельности судов является полное исключение, предупреждение развития ударного характера передачи движущей силы буксируемому судну. Достигается это установкой в корпусе демпфирующего устройства в виде упругой вставки, степень жесткости которой была бы в 51 раз меньше жесткости, упругости корпуса судна. Этим обеспечивается степень повышения рентабельности судна в 7.1 раза, как корень квадратный из степени уменьшения жесткости корпуса, и увеличение крейсерской скорости судна в 2.67 раза, как корень квадратный из степени повышения рентабельности.

Принятая жесткость упругой вставки не только нейтрализует ударный характер движущей силы, но и нейтрализует возникновение лобового сопротивления движению судов.

Суда, оборудованные устройством [5], при движении по воде не создают судовых волн, а при движении в воздухе – ударной звуковой волны, слоя сжатого воздуха повышенной плотности перед фюзеляжем.