Оптимизация территориального размещения малых электростанций

Освоение возобновляемых источников энергии (ВИЭ) и замена ими традиционной углеродной энергетики является сегодня одним из главных стратегических направлений развития мировой энергетики. При этом мощности электростанций (ЭС), использующих ВИЭ, как правило, довольно небольшие. Даже гидроэнергетика, давно используемая и хорошо исследованная, относится к ВИЭ, только при мощности ГЭС не выше 30, а иногда и 10 МВт. Такая же ситуация и с другими основными видами ВИЭ – ветро, солнечной, био и пр.

Таким образом, успешное освоение ВИЭ возможно только путем массового строительства ЭС небольшой мощности. Это требует правильного их территориального размещения. Критерием оптимизации при этом будет минимиза­ция общих затрат на строительство ЭС и линий электропередач (ЛЭП) и эксплуатационных издержек, в том числе связанных с потерей электроэнергии в ЛЭП.

В настоящей статье вопросы оптимизации размещения ЭС рассматриваются применительно к малой гидроэнергетики, - малых ГЭС (МГЭС). Но используемые при этом методы и результаты могут быть применены также к любым другим источникам ВИЭ.

Оптимизации размещения источников ВИЭ будет обеспечена, если зона влияния ЭС будет ограни­чиваться расстоянием, стоимость передачи электроэнергии на которое путем строитель­ства ЛЭП с учетом потерь электроэнергии будет дешевле сооружения новой станции требуемой мощности.

Критерием такого подхода является радиус эффективности электростанции R_эфф. Он определяется из условия, что в пределах круга этого радиуса энергообеспечение локального потребителя за счет уже существующей в его центре ЭС будет дешевле строительства новой ЭС на месте потребления.

Затраты на реализацию первого варианта энергообеспечения потребителя (строительство ЭС) включают в себя стоимость строительства ЭС необходимой мощности N непосредственно на месте потребления и эксплуатационные затраты на ее обслуживание:

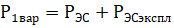
или:

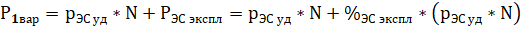     (1)

где: Р_ЭС – общая стоимость строительства ЭС, мощностью N, долл.

Р_{ЭС уд} - удельная стоимость строительства ЭС, долл/Вт.

Р_{ЭСэкспл} – ежегодные затраты на эксплуатацию ЭС. Обычно принимаются в процентах от стоимости ЭС, %_{ЭС экспл} = 2-3%.

N – мощность, Вт.

Во втором варианте (строительство ЛЭП) общие затраты будут состоять из стоимости строительства ЛЭП, протяженностью L (от уже существующей станции до потребителя), эксплуатационных затрат на обслуживание ЛЭП плюс стоимость потерь электроэнергии на ее доставку:

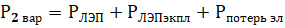
или:

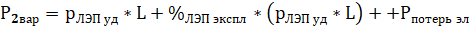    (2)

Р_ЛЭП – общая стоимость строительства ЛЭП, длиной L км, долл.

р_{ЛЭП уд} - удельная стоимость строительства ЛЭП, долл/км.

Р_{потерь эл} – стоимость потерь электроэнергии в ЛЭП, долл/год:

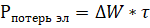     (3)

ΔW – годовые потери электроэнергии в ЛЭП, Вт.ч/год [15],

т – тариф на электроэнергию, долл/Вт. ч,

Р_{ЛЭП экспл} – ежегодные затраты на эксплуатацию ЛЭП (также, как и для ЭС обычно принимаются в процентах от стоимости ЛЭП, %_{ЛЭП экспл} – 2-3%).

Потери электроэнергии в ЛЭП для одной фазы трехфазного тока можно определить известным способом [1, 2][1].

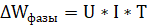      (4)

где: U – среднее напряжение линии за рассчитываемый период, В,

I – ток в линии, А,

Т – рассматриваемый период времени, час,

где напряжение U можно представить в виде:

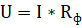     (5)

R_ф –электрическое сопротивление одной фазы ЛЭП, равное:

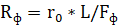    (6)

L – длина линии, км,

r_o – удельное сопротивление провода, Ом*мм²/км

F_ф – сечение провода одной фазы, мм²,

Подставляя (5) и (6) в (4), получим:

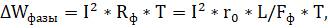      (7)

где значение тока I, протекающего по ЛЭП, может быть найдено, как:

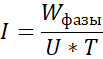    (8)

W_фазы – значение активной составляющей потребляемой одной фазой электроэнергии за рассчитываемый период времени, Вт.ч, равное:

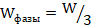     (9)

W – полное (для всех трех фаз) значение активной составляющей потребляемой электроэнергии за рассчитываемый период времени Т, Вт.ч.

Подставляя (8) в (7) и учитывая при этом наличие реактивной мощности в сети и неравномерность графика потребления [3] будем иметь:

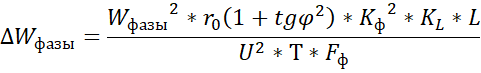       (10)

где: tgφ – коэффициент реактивной мощности (0,6),

К_ф² - коэффициент заполнения графика:

K_ф² = (1 + 2К_з)/3K_з

К_з – коэффициент заполнения графика (при отсутствии данных о форме графика нагрузки обычно принимается значение - 0,3; тогда: K_ф² = 1,78).

К_L – коэффициент, учитывающий распределённость нагрузки по линии (0,37 - для линии с распределённой нагрузкой).

Общие потери электроэнергии ЛЭП (суммарно для трех фаз) равны:

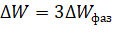
Учитывая (9) и то, что W = N*T, где N – передаваемая мощность, а также принимая:

F = 3F_ф

где: F – суммарная площадь сечения всех трех фаз,

и объединив все три коэффициента в один:

К_общ =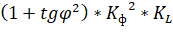 

окончательно будем иметь:

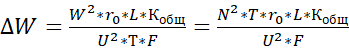      (11)

Стоимость строительства ЭС и ЛЭП, — это одноразовые капитальные вложения, в то время как эксплуатационные затраты, в том числе потери электроэнергии, — это ежегодные издержки. Для того чтобы учесть это различие, в экономических расчетах сравнительной эффективности двух рассматриваемых вариантов воспользуемся методом приведенной стоимости[2] [4, 5]:

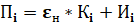    (12)

где: П_I – приведенные затраты в i-ом варианте,

К_i – капиталовложения в i-ом варианте,

И_i - ежегодные издержки в i-ом варианте,

ε_н – нормативный коэффициент эффективности использования капитальных вложений (в энергетике - ε_н = 0.12).

При таком подходе, учитывая, что в обоих вариантах все эксплуатационные издержки кроме стоимости потерь электроэнергии рассчитываются в процентах от соответствующих капиталовложений (3%), их можно учесть, просто приняв с запасом:

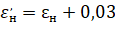 = 0,15.

После этого критериальное уравнение (1) в приведенных стоимостях будет иметь вид:

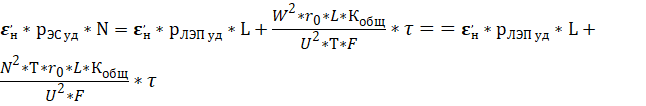(13)

R_эфЭС будет являться решением уравнения (13) относительно L:

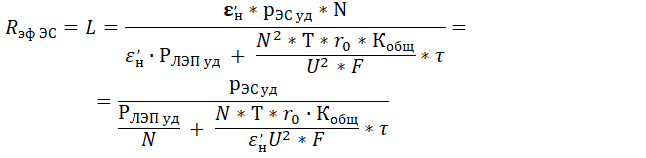(14)

В соответствие со смыслом приведённой стоимости (формула 12) в этой и во всех формулах ниже Т – время расчета издержек (в нашем случае потери электроэнергии и эксплуатационных затрат) равно времени, соответствующему одному году. Хотя Т, в принципе, может назначаться произвольно, но с условием его взаимно однозначного соответствия с нормативным коэффициентом окупаемости ε_n, так как ε_n является обратной величиной срока окупаемости Т_ок, определяемой из выражения:

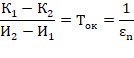
где размерность К – [долл.], а И_i – [долл/год].

В электроэнергетике при этих условиях, на основе опыта строительства принимается, что предельный срок окупаемости успешных проектов равен 8 лет. Отсюда получаем ε_n≈0.12.

Таким образом время расчета издержек Т и нормативный коэффициент окупаемости ε_n жестко связанные между собой величины. Принимая ε_n=0,12, мы одновременно должны принять время расчета издержек, Т = 1 год.

На первый взгляд это противоречит здравому смыслу – мы искусственно ограничиваем параметр Т. Но на самом деле, параметр Т, входит во все полученные в этой статье расчетные формулы только в виде частного Т/ε_n, что снимает это противоречие.

Это можно показать следующим образом. Если уменьшить расчетный срок расчета издержек, например, в два раза (с одного года до полугодия), то это при неизменных капитальных вложениях приведет к увеличению в два раза нормативного срока окупаемости: Т_ок = 16 полугодий и соответственно такому же уменьшению ε_n. Таким образом отношение Т/ε_n останется тем же самым.

Также можно отметить, что если при определении приведенной стоимости использовать в качестве расчетного периода не год, а полугодие, то добавка, учитывающая эксплуатационные затраты также уменьшится в два раза и станет равной не 0,03, а 0,015. При этом останется прежнем не только отношение Т/ε_n но и 

Если потребитель находится внутри круга радиуса R_эфЭС., в центре которого расположена действующая ЭС достаточной мощности, то целесообразно запитать его от этой, уже существующей ЭС. В противном случае более выгодно построить новую ЭС в непосредственной близости от потребителя.

Все входящие в формулу (14) параметры однозначно определяются конкретными условиями решаемой задачи. Исключение составляет только сечение провода ЛЭП – F (или F_ф), который сам требует оптимизации.

Критерием оптимизации F является минимизация общей стоимости провода, сечением F и потерь электроэнергии в ЛЭП с проводами такого сечения [6]:

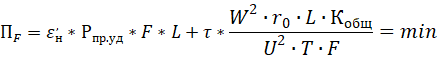     (15)

где: Р_{пр уд} – удельная стоимость провода.

Экстремум этого выражения, как функции сечения провода, F, достигается при равенстве нулю ее производной:

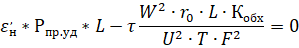
или:

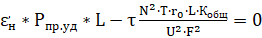     (16)

Так как вторая производная 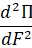 ˃ 0, то этот экстремум в данном случае представляет собой минимум. Значение F, которому соответствует этот минимум, является оптимальным, при нем достигается минимум приведенных затрат.

Решая (16), получим:

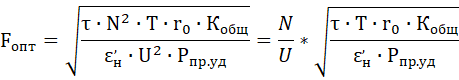     (17)

В формуле (17) первый сомножитель, — это ток I (N/U = I), в Амперах, а второй – постоянная для любого конкретного случая величина, размерность которой (А/мм²)^-1. То есть, сечение F_опт в (17) определяется, по сути дела, по плотности тока.

Подставив значение F_опт (17) в формулу для R_эф (14), получим:

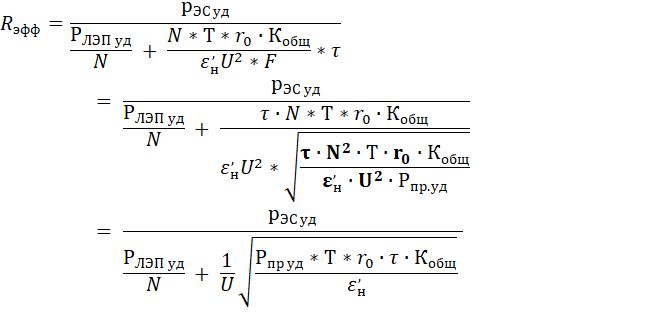(18)

Формула (18) показывает, что R_эф прямо пропорционален Р_{ЭС уд} и для всех конкретных случаев у R_эф есть асимптота - с ростом N, первое слагаемое знаменателя уменьшается и в конце концов становится пренебрежимо малым, после чего значение R_эф приобретает постоянное, независимое от N значение. Как видно из формулы (18), в этом случае асимптоты R_эф прямо пропорциональны напряжению ЛЭП, U.

То же самое имеет место и по отношению к напряжению ЛЭП, U. При увеличении мощности ЛЭП, U, радиус эффективности в формуле (18) асимптотически стремится к значению, равному:

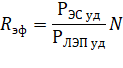
то есть становится прямо пропорциональным мощности N. Например, при больших мощностях N, для которых только и используются высоковольтные ЛЭП, значения R_эф достигают тысяч и десятков тысяч километров, то есть становятся практически неограниченными, что, собственно, и подтверждается на практике.

Также можно отметить, что при постоянном напряжении U оптимальные сечения проводов в соответствии с (17) также прямо пропорциональны мощности N.

При расчетах R_эфф и F_опт также нужно учесть, что удельная стоимость ЭС, Р_ЭС.уд и тариф на электроэнергию, τ, взаимосвязаны друг с другом зависимостью [7]:

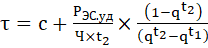     (19)

где: Р_ЭС.уд = удельная стоимость строительства ЭС, долл/Вт

t₂ – срок строительства ГЭС, лет,

t₁ – жизненный цикл проекта, лет

Ч – число часов использования установленной мощности ЭС в год,

т – тариф на электроэнергию, долл/Вт·ч

с – себестоимость электроэнергии, долл/Вт·ч

Таблица 1

q =	0,9	—
c =	0,005	долл/кВт.ч
t2 =	2	год
t1 =	30	лет
Ч =	5000	час/год

Для стандартных для МГЭС значений параметров, приведенных в табл. 1, тариф, обеспечивающий безубыточности строительства МГЭС, рассчитанный по формуле (19), равен 0,07435657 долл/кВт.ч. Но это тариф окупаемости, который обеспечивает только возврат затрат на строительство ЭС. Нужно учесть также налоги для государства, оптимальная величина которых (рис. 1) зависит от стратегии развития энергетики – планируемого роста мощности системы [8].

При планируемом росте мощности энергосистемы малых ЭС в 5 раз, по графику на рис. 1, находим, что для этого случая оптимальное значение α, обеспечивающее такой рост мощности при одновременной максимизации налогов для государства будет равен 0,5142. Отсюда полный тариф для этого случая должен быть:

0,07435657/0,5142 = 0,14460632 долл/кВт.ч = 0,000145 долл/Вт.ч

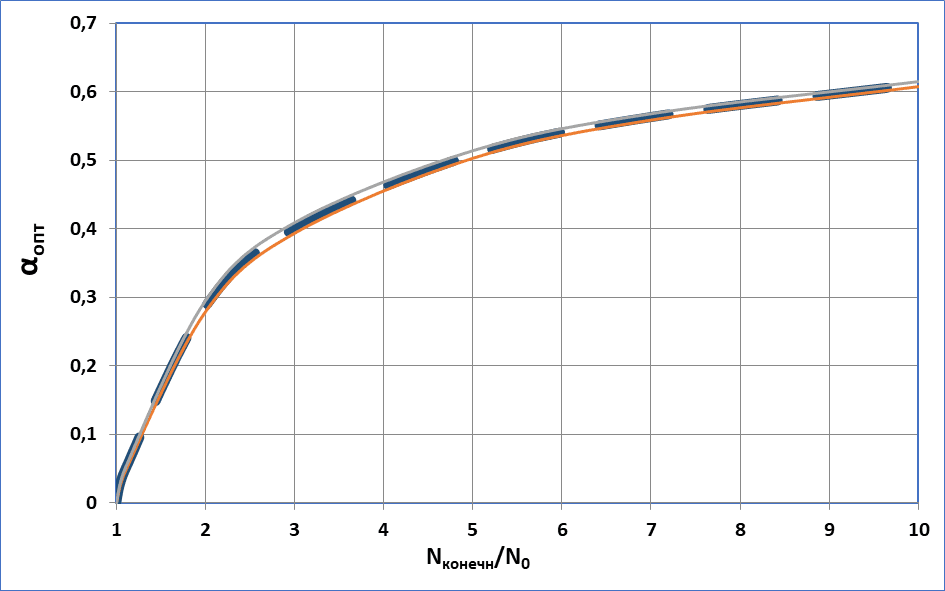
Рис. 1. α_опт = f(N_конечн/N₀)

Таблица 2

Рэс уд =	3	долл/Вт
Р пр уд =	30	долл/км*мм2
Т =	8760	час
r0 =	28	Ом*мм2/км
τ =	0,000145	долл/Вт*час
Кобщ	0,895696	—
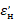	0,15	—

На рисунках 2 и 3 (в более крупном масштабе) показаны результаты расчетов радиуса эффективности МГЭС R_эфф (формула 18), как функции мощности N, для трех значений напряжения: 0,38, 6 и 10 кВ, с удельной стоимостью ЛЭП, соответственно равной 10500, 14500 и 17000 долл/км [9, 10], при других параметрах в соответствие с таблицей 2.

Соответствующие этим значениям R_эфф оптимальные сечения отдельных фаз проводов ЛЭП, F_{фазы опт}, рассчитанные по формуле (17) показаны на рис. 4.

Результаты, представленные на рис. 2, 3, 4, получены расчетом R_эфф по формуле (18) и F_опт по формуле (17).

Но выбор сечения провода F, может быть сделан не путем оптимизации затрат (формула 17), а непосредственно по плотности тока:

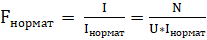     (20)

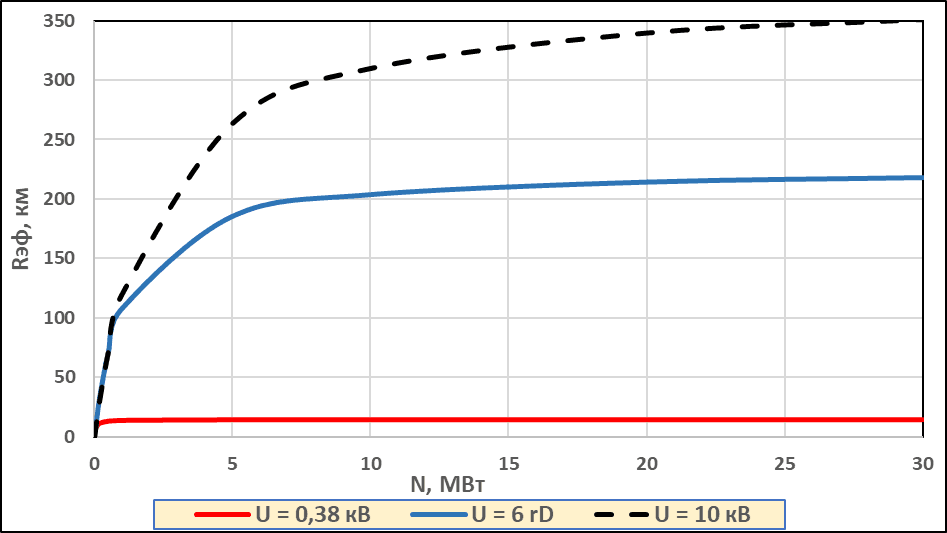
Рис. 2. R_эф = f(N)

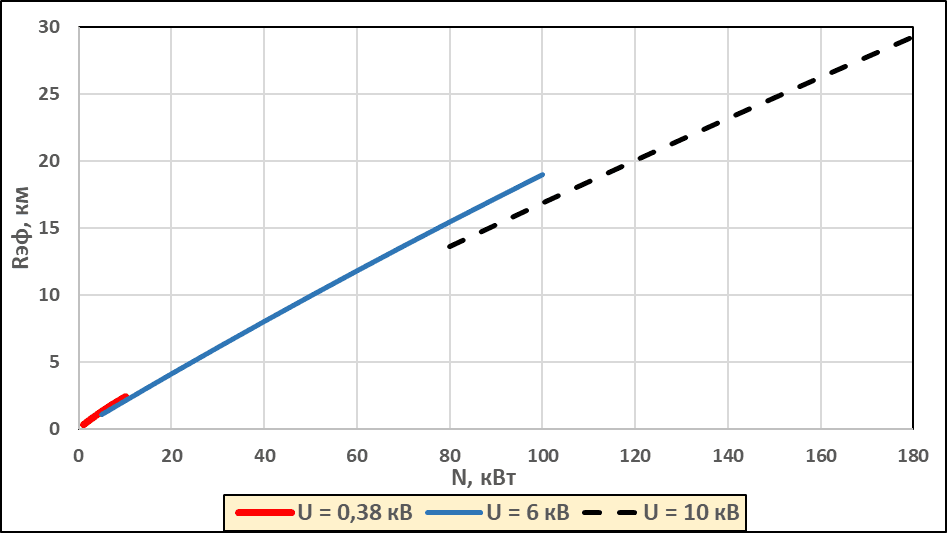
Рис. 3. R_эф = f(N)

В этом случае радиус эффективности R_эфф будет определяться выражением:

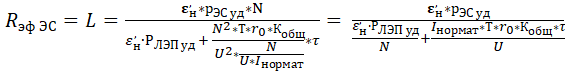     (21)

Расчеты показывают, что в этом случае результаты (рис. 2, 3, 4) будут теми же самыми, если принять:

I_нормат = 0,3759 А/мм²

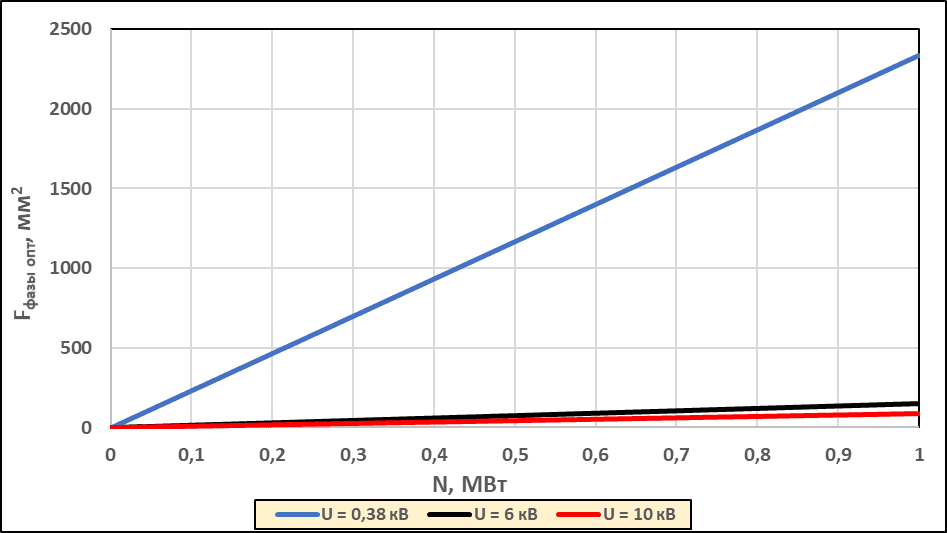
Рис. 4. F_{фазы опт} = f(N)

ВЫВОДЫ

Предлагаемый в настоящей статье метод совместной оптимизации строительства МГЭС и ЛЭП по основным влияющим параметрам (мощность ЭС, стоимость строительства и эксплуатации ЭС и ЛЭП, сечение провода, тариф на электроэнергию, налоги и пр.) позволяет выбрать вариант энергоснабжения потребителей, минимизирующий стоимость и одновременно обеспечивает окупаемость строительства ЭС.

Полученная в результате оптимизации затрат и издержек формула для расчета максимального радиуса эффективности R_эфф (18) позволяет решить вопрос выбора наиболее выгодного территориального размещения ЭС, одновременно обеспечивая выбор наиболее эффективного сечения провода ЛЭП. Само это сечение провода, F, может быть найдено по формуле (17).

[1] Потери на корону при этом не принимаются во внимание ввиду их незначительности при рассматриваемых напряжениях ЛЭП

[2] В принципе, тоже самое выражение (12) мы будем иметь и в случае более современного подхода – приняв нормируемое значение дисконта или установив его социальную норму. В частности, норма дисконта для малых ЭС и ЛЭП для них, соответствующая сроку окупаемости 8 лет (и, соответственно, ε_н = 0,12), равна 0,1.