Оптимизация маршрутов поставок продукции ОАО «1-я Минская птицефабрика»

Предприятие ОАО «1-я Минская птицефабрика» является одним из основных поставщиков яйца куриного в торговую сеть г. Минска. Современная технология поставки продукции предусматривает ежедневную доставку продукции в многочисленные торговые точки города по заявкам предприятий торговли. В связи с нестабильным спросом на продукцию транспортному подразделению птицефабрики ежедневно требуется строить маршруты доставки продукции от склада до торговых точек. Снижение транспортных затрат на эту доставку может быть достигнуто применением информационных технологий в организации транспортной логистики ОАО «1-я Минская птицефабрика».

ОАО «1-я Минская птицефабрика» осуществляет поставку яиц в крупнейшие магазины города Минска и Минского района со склада, расположенного на территории предприятия в агрогородке «Большевик», Минского р-на. Торговые точки с адресами представлены в таблице.

Таблица

Реализация яйца куриного ОАО «1-я Минская птицефабрика» (магазины г. Минска и Минского р-на)

В короб для доставки продукции помещается входит 25 кг яйца куриного. Поэтому данные в четвертом столбце таблицы пропорциональны 25. Общий объем заказанной продукции составляет 1900 кг. Следовательно, для доставки продукции в торговые точки необходимо использовать два автомобиля – фургона, имеющих каждый грузовместимость 1 т. Характер каждого маршрута кольцевой, т.е. перевозки осуществляются по замкнутому маршруту.

Исходя из приведенных данных, необходимо рассчитать оптимальные маршруты для доставки продукции. В математическом программировании подобная задача получила название «задача коммивояжера» [1, 2, 3]. Для ее решения необходимо построить матрицу расстояний между всеми рассматриваемыми пунктами, затем занести ее в выбранную компьютерную среду, например, MATLAB (рис. 1) и присвоить ей некоторое имя, например, A.

Далее поиск оптимального маршрута движения осуществляется путем применения процедуры MatLab vrpsaving (vrp – vehicle routing problem) (рис. 2) [1]. Эта процедура реализует алгоритм Кларка – Райта [2, 3]. Достоинством этой процедуры является возможность построения для совокупности рассматриваемых пунктов группы оптимальных маршрутов, если перевозку грузов нельзя выполнить одним транспортным средством, недостатком – приближенный характер алгоритма.

В этой процедуре:

A – вышеуказанная матрица расстояний, км;

TC (total costs) – длина искомого маршрута, км;

rte (route) – искомая последовательность пунктов в маршруте, вывод этой последовательности на экран осуществляется опцией rte{1}.

В той же среде следует задать величину Q, равную грузовместимости автомобиля: Q = 1000 и вектор размерности 1˟20, элементами которого являются данные четвертого столбца таблицы.

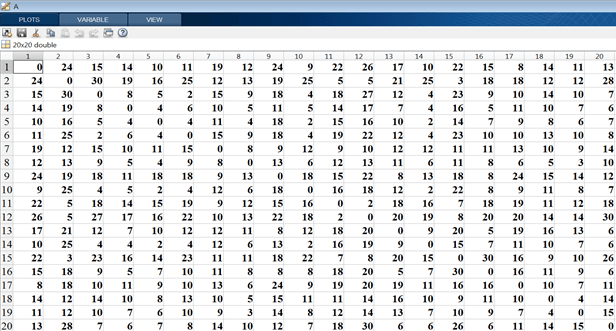
Рис. 1. Матрица расстояний между пунктами, км

Из решения, представленного на рисунке 2, следует, что длина оптимального маршрута составляет 112 км. Последовательность пунктов оптимального маршрута соответствует их нумерации в таблице.

Решение рассматриваемой задачи также может быть также выполнено в компьютерной среде MS Excel, с помощью функции ИНДЕКС и процедуры Поиск решения. Алгоритм решения представлен на рисунке 3.

Рис. 2. Расчет оптимального маршрута по процедуре vrpsaving в среде MatLab

Решение задачи по алгоритму, представленному на рисунке 3, дает более оптимальный маршрут доставки яиц из грузоотправляющего пункта (Минский р-н, а.г. Большевик) в магазины г. Минска: 1-17-8-19-18-15-2-12-11-7-9-16-13-20-4-5-14-6-3-10-1. Длина маршрута составляет 108 км.

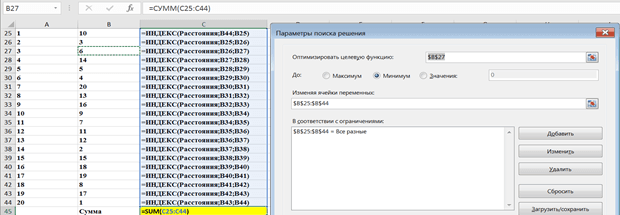
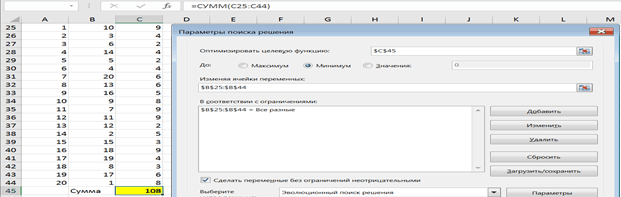
Рис. 3. Расчет оптимального маршрута по процедуре “Поиск решения” в среде MS Excel