При приближении синуса (и не только) полиномамы Чебышёва используют следующее выражение:
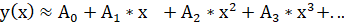
где коэффициенты A0, A1 и т.д. рассчитываются заранее, например как написано здесь https://habr.com/ru/post/577256/.
Для рядов Макларена синус вычисляется по следующей формуле:
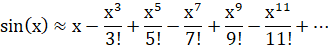
Для сокращения вычислений можно вынести повторяющиеся фрагменты за скобки. Например, так:
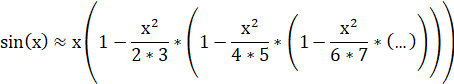
или так:
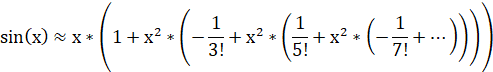
Коэффициенты при x можно посчитать заранее и сохранить в таблице с тем, чтобы при вычислении осталось только умножать и прибавлять.
Для примера найдём значения синуса на интервале от о до 2π обеими методами, и построим их графики вместе с графиком "настоящего" синуса.
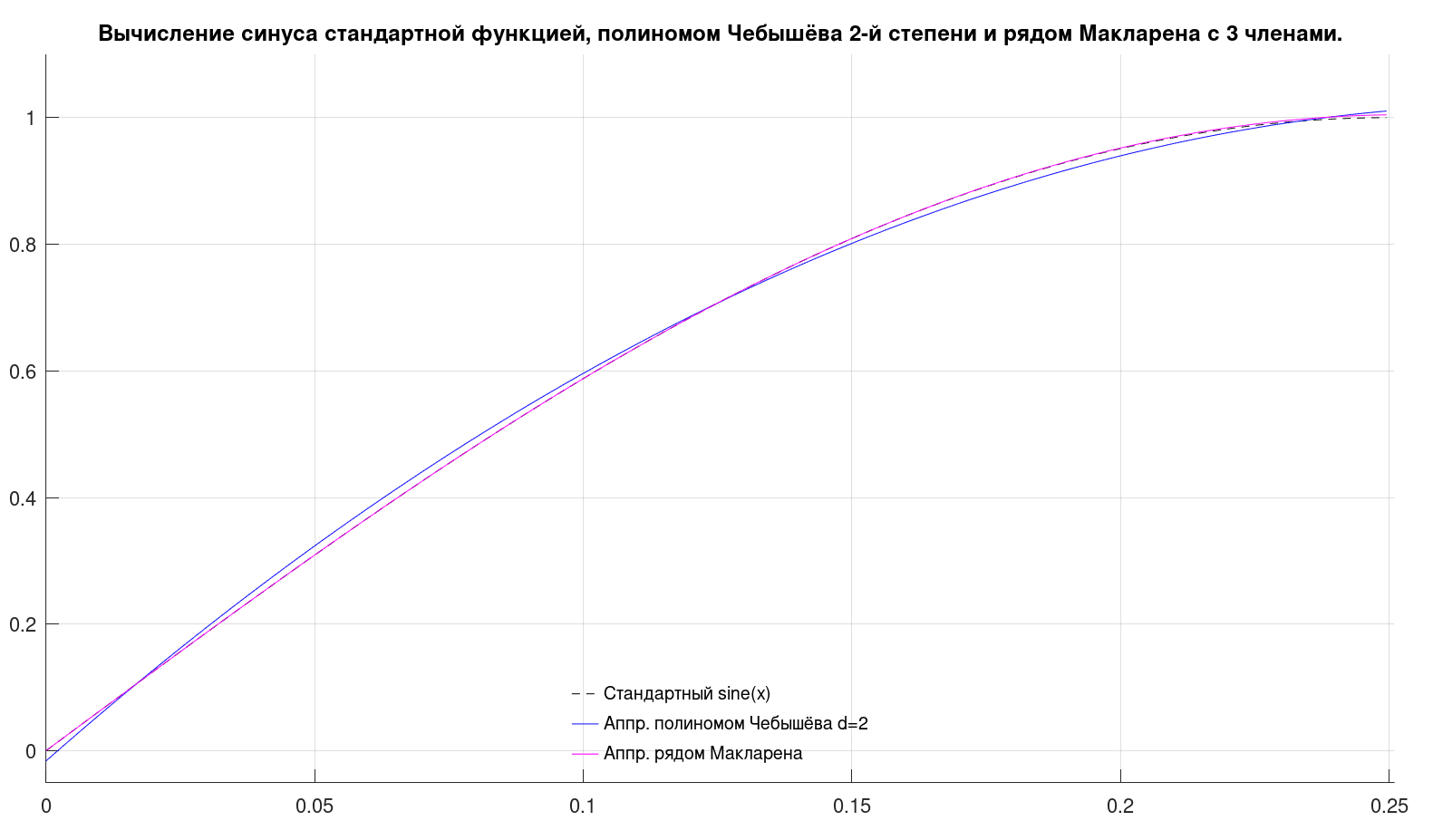
Рис. 1
График многочлена Чебышёва (синяя линия) представляет собой фрагмент параболы, и пересекает график синуса в трёх точках, являющимися корнями многочлена.
График ряда Макларена (сиреневая линия), начиная с левого края, почти совпадает с графиком синуса, и расхождение с ним начинается заметно на глаз только в правой трети диаграммы.
Графики ошибок аппроксимации синуса от самого синуса выглядят так.
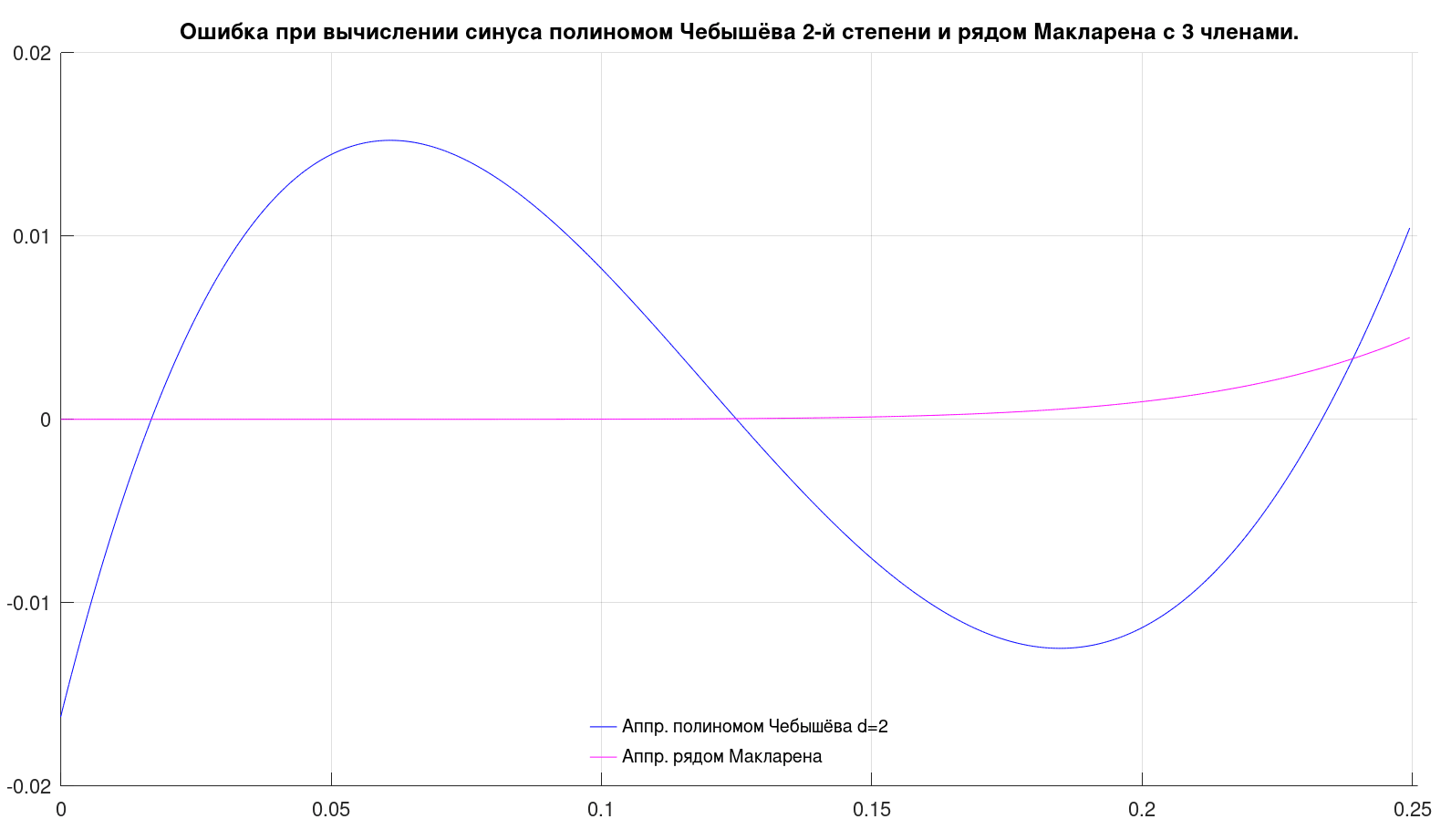
Рис. 2
Видно, что ошибка приближения полиномом Чебышёва в разы больше таковой у ряда Макларена.
Теперь давайте посмотрим, как ошибки аппроксимации зависят от количества членов аппроксимирующей функции.
Графики ошибок аппроксимации рядами Макларена разной длины выглядят так:
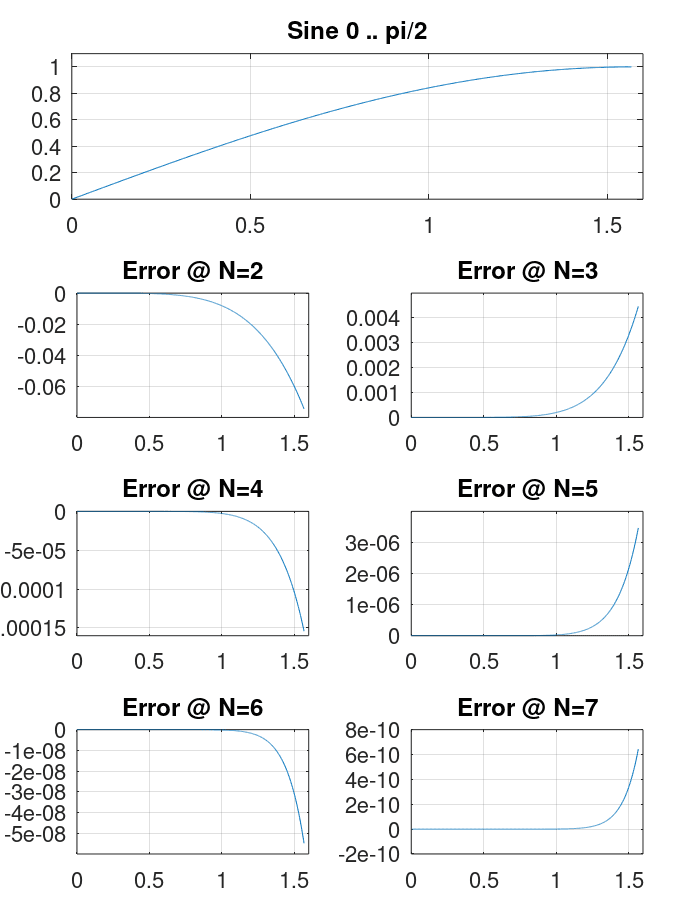
Рис. 4
Графики ошибок аппроксимации полиномами Чебышёва имеют следующий вид:
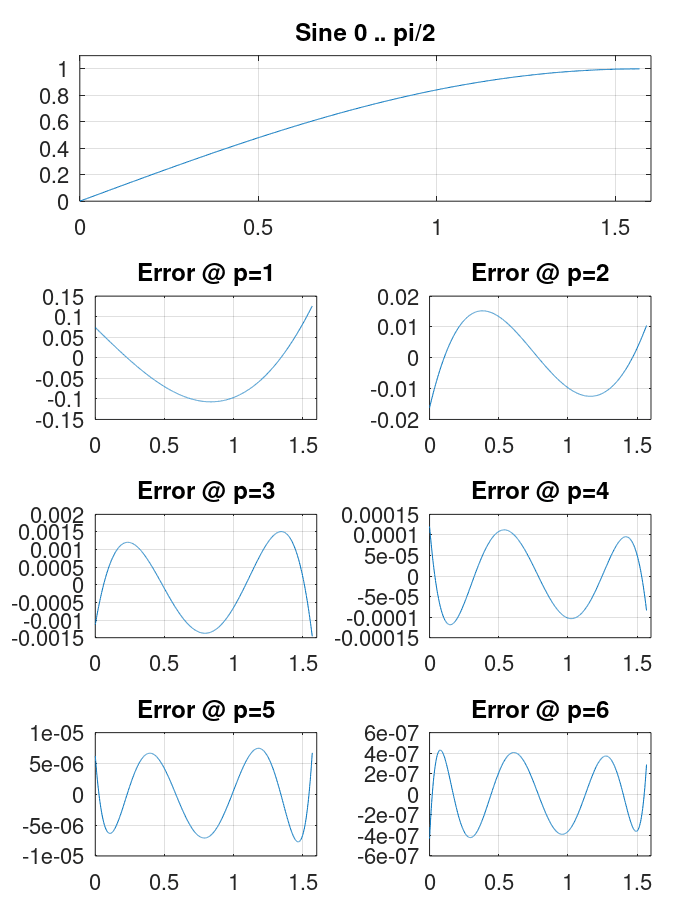
Рис. 5
Графики ошибок выглядят по-разному, но в обоих случаях величина ошибки падает с увеличением количества членов ряда.
На следующей диаграмме показана сравнительная точность аппроксимации обоими методами в зависимости от количества членов ряда (полинома).
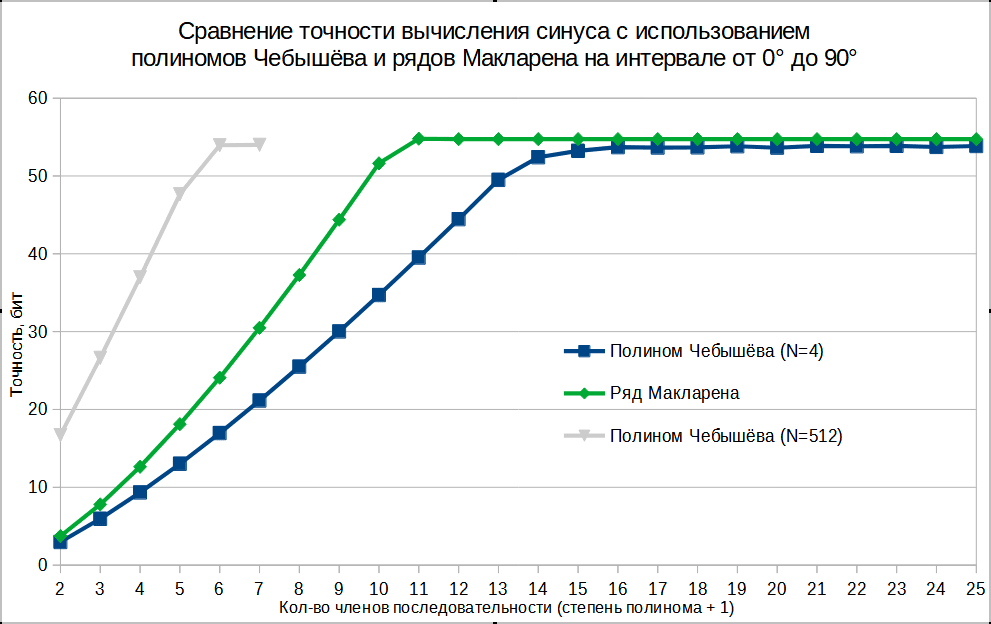
Рис. 6
Точность выражена в "дробных битах", и численно равна минус логарифму ошибки по основанию 2:
Ebit= -log2(|E|)
Вычисления производились с использованием 80-битных числе с плавающей запятой (тип long double). Результаты аппроксимации сравнивались со значением синуса, полученными стандартной функцией sinl() библиотеки языка С.
На диаграмме видно, что приближение при помощи рядов Макларена (зелёная линия) даёт большую точность по сравнению с полиномами Чебышёва (синяя линия). Точность не растёт выше какого-то предела, это связано с ошибками округления при вычислениях.
Однако для аппроксимации полиномами Чебышёва полный период (от 0 до 2π) можно разбить не на 4, как это делалось во всех предыдущих вычислениях, а, например, на 512 равных интервалов. На диаграмме этот случай представлен серой линией. Точность в 53.94 бита при 6 членах (соответствует полиному 5-й степени) превышает таковую у ряда Макларена (51.62 бита) при 10 членах ряда. Но при этом, надо отметить, страдает такое свойство функции, как непрерывность, т.к. на границах интервалов будут разрывы, что в некоторых случаях может быть критичным.
Какой из двух методов использовать для аппроксимации? Это зависит от нескольких условий. Если требуется непрерывность функции, следует использовать ряды Макларена, т. к. этот метод даёт большую точность, особенно при малых значениях аргумента.
Если требуется максимальное быстродействие, следует использовать полиномы Чебышёва с разбиением периода на интервалы. Количество интервалов и степень полинома можно выбрать, исходя из необходимой точности.

.png&w=640&q=75)