Задача курса математики средней школы – обеспечить прочное и сознательное овладение основами математических знаний, умений и навыков, необходимых для общего развития учащихся, для их практической деятельности. Программа по математике предоставляет учителю широкие возможности для выбора различных методических путей и приемов изложения материала. Получают развитие те методы преподавания, которые способствуют повышению у учащихся интереса к изучению математики, сознательному усвоению ими математических понятий, стимулируют активность учащихся, воспитывают в них навыки самостоятельной работы, умение рационально и творчески выполнять полученные задания, самостоятельно приобретать знания.
Дать каждому ученику глубокие и прочные знания – задача, требующая постоянного совершенствования собственных знаний учителя и серьезного продумывания всех элементов учебного процесса. Основной стимул учения – интерес к знаниям, и он должен систематически развиваться у каждого ученика.
Главным условием формирования познавательной активности школьников является содержание и организация урока. Отбирая материал и продумывая приемы, которые будут использованы на уроке, учителю надо оценить их с точки зрения возможности возбудить и поддержать интерес учащихся к предмету. Основным фактором развития интереса к предмету является понимание учащимися излагаемого материала и успешное выполнение ими предлагаемых упражнений. Выполняя задание, ученик не исходит только из его полезности. Если он справляется с предлагаемым материалом, он любит это дело. В действительности любить тот или оной предмет у него равносильно умению сделать ту или иную работу. Чтобы предупредить непонимание изучаемого материала, учителю важно не только подобрать материал и продумать методику его изложения, но и все время быть в курсе того, насколько он усвоен каждым учеником. Этого можно достичь лишь при условии «дробного» контроля за работой ученика и оказания ему своевременной помощи.
Важным средством познавательной активности к самостоятельности учащихся является применение различных самостоятельных работ, тренировочных, контрольных. Большую пользу в отборе самостоятельных работ оказывают дидактические материалы по математике во всех классах. Остановимся на некоторых видах самостоятельных работ.
- Самостоятельная работа по образцу. Они полезны для закрепления нового материала, создают условия для перехода ученика к выполнению заданий, требующих более высокого уровня знаний.
- Самостоятельные работы с указаниями к решению. При их выполнении предполагается известная самостоятельность в выборе пути решения задачи: ученик получает лишь указание, облегчающее выполнение этого пути.
- Самостоятельные работы, помогающие разобраться в доказательстве теоремы и лучше усвоить ее, помогающие разобраться в решении задач.
- Самостоятельные работы с выбором ответа. Эти работы применяют при подготовке учащихся к восприятию нового, так и при закреплении пройденного. Примером таких работ является следующая:
Задание 1. Решить неравенство 18 – 5х < 12.
Ответы:
х< -5 (0) х > 5 (1) х < -6 (2) х > 3,5 (3) х >1,2 (4) х < 5 (5) | х <1,2 (6) х < 3,5 (7) х > -6 (8) х > -5 (9) Код 0, 1 , 2, 3, 4, 5, 6, 7, 8, 9 |
Задание 2. Решить неравенство а (а – 4) - а² > 12 – 6а
Ответы:
а < -17; а > 9; а <6; а <4 ; а > -1,2; а < 9; а > 6; а >4
; а > -1,2; а < 9; а > 6; а >4 ; а < - 1,2; а > -17.
; а < - 1,2; а > -17.
Код 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Задание 3. Решить неравенство х – 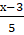 +
+ 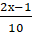 < 4
< 4
Проверка: назвать код от трех заданий (ответ:462).
В ответах предлагаются те варианты, которые получаются в случае, если учащиеся допускают типичную ошибку. По названному коду учитель может судить о качестве работы.
Большую помощь в контроле за пониманием материала могут оказать и математические диктанты, которые можно проводить на разных этапах урока, как по алгебре, так и по геометрии.
Например, в 7 классе на свойства неравенств может быть проведен диктант:
- Записать неравенство 3х > 2 и 3х < 2.
- Записать неравенство 7 > 3; 3 > -1. Записать верное неравенство, пользуясь свойством транзитивности.
- Записать верное неравенство, которое получается из верного неравенства 3 > 2, если прибавить к обеим частям – 7 и т. д.
Большую роль в активизации мыслительной и познавательной деятельности учащихся играет решение задач по готовому чертежу на уроках геометрии. Устное решение задач по готовым чертежам увеличивает число задач, разобранных в классе, развивает пространственное воображение учащихся и прививает навык отыскания различных путей решения, что влечет за собой повторение большого объема пройденного ранее материала.
Сознательное усвоение материала – необходимое условие активной мыслительной деятельности учащихся. На мыслительную деятельность активно воздействуют многие виды устных упражнений, такие как упражнения, стимулирующие логическое мышление. К ним можно отнести упражнения, включающие элементы исследования. Развитие логического мышления невозможно без четкого усвоения определений, изучаемых в курсе математики средней школы.
Нужно упомянуть и еще об одном виде упражнений, при выполнении которых учащиеся оперируют понятиями математики, получают возможность творческого подхода к изучению математики – это самостоятельное составление задач, упражнений, теорем. Начинать этот вид упражнений надо с простых заданий по аналогии, постепенно усложняя их. Например, составить многочлен, где есть буквы а и х; с коэффициентами 2, 4 и 5.
В работе перечислены лишь немногие виды работ, активизирующие мышление учащихся. Их очень много. И каждый учитель должен являться творцом на своем уроке, отбирая на каждый свой урок нужные упражнения, приемы.

.png&w=640&q=75)