Mathematics and economics are two independent branches of knowledge, each of which has its own object and subject of study. According to the famous American scientist N. Wiener, the role of mathematics is to find invisible order in the chaos that grips us.
Consequently, mathematics as a science creates multifunctional analytical methods for studying connections and acquiring, on this basis, the latest information about the world around us. Currently, those areas of knowledge that most extensively use mathematical methods in their research are achieving the highest successes. After all, mathematics has terms that, at first glance, have no direct relation to real life: matrices, integrals, equations, etc. Mathematics, as a distinctive field of knowledge, has features that make it unique. These include the following:
- certain rules for creating relationships – mathematical formulas;
- when deriving formulas, a number of axioms are first drawn up, and then, proceeding from them, on the basis of the strictest conditions, mathematical formulas are drawn up;
- the ability to own certain terms without revealing their meaning [1].
Following from the above features, it is they that make the mathematical apparatus a multifunctional analytical tool for all branches of knowledge. In other words, with the help of mathematical transformations on the basis of hypotheses and logical rules, it is possible to establish the latest properties and relations of real objects, which can then be empirically confirmed. This makes mathematics the queen of sciences. As Karl Marx said, science achieves perfection only when it manages to use mathematics. Economics poses little-known problems to mathematics and develops an interest in finding ways to solve them. At present, the needs of economics for new mathematical methods outstrip the abilities of mathematics. Economic reality revealed the origin of entire directions in applied mathematics - game theory, programming, queuing, etc. The development of mathematical methods is becoming a characteristic element of the development of highly professional knowledge of specialists in the field of economics and management. It is known that in the current situation in connection with the increasing importance of applied mathematics in economics, the origin of the latest special technologies for mathematical information processing, it is imperative to revise the content of mathematics courses. The user needs to know and be able to, not how exactly the mathematical formula is obtained, but where and under what conditions it can be applied in economics.
Problems with economic content can be solved in different ways: using the formulas of simple and compound interest [2], in general, using degrees. The article considered a simple way to solve banking problems for loans using progression formulas. The initial loan size is designated as A, the bank's percentage is taken as r %. The annual payment on the loan will be equal to X, then a year after the accrual of interest and payment of the amount X, the amount of the debt will be [3]:
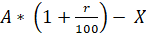(1)
We denote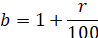 
Therefore, after 2 years, the amount of the debt will be: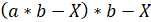 
;
in three years: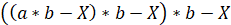 
;
in n years: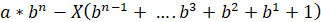 
.
To calculate the value in parentheses, it is convenient to apply the formula for the sum of n terms of a geometric progression.
The formula for the sum of n terms of a geometric progression is as follows: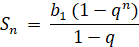 
, then the amount of debt in n years is:
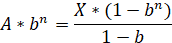(2)
Let's look at some sample tasks:
Let Arman borrowed 569,000 tenge from the bank on January 10 at 14.5% per annum. The payment scheme is as follows: on January 10 of each next year, the bank charges interest on the remaining debt (that is, increases the debt by 14.5%), then Arman transfers X tenge to the bank. What should be the amount X for Arman to pay off the debt in two equal annual installments? [n2]
Solution: If the loan amount is A, the interest rate is r, the annual payment (tranche) is X, the number of years for which it is planned to repay the loan n, then the amount of payments using formula (2) will be:
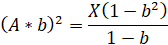
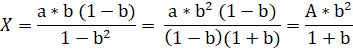
where
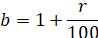(3)
Substituting these tasks into the formula (3):
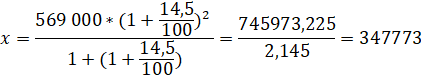
Answer: 347,773 tenge per year.
Next, consider a similar task:
On January 20, 2021, the client took out a loan from the bank on the following conditions:
- loan term 24 months;
- on the 1st day of each next month, the debt increases by 1.2% compared to the end of the previous month;
- from the 12th to the 19th of each month, part of the debt should be repaid, so that on the 20th of each month, the debt is reduced by the same amount.
What amount was taken on credit if it is known that the total amount of payments is equal to 1,035,000 tenge? [4, 5]
The solution of the problem:
The total amount of payments can be divided into two parts: the principal debt (the amount taken on credit) and the interest payment. Moreover, the main debt is divided into 24 equal payments. For clarity, let's draw up a table (table), having previously designated for x tenge - the amount taken on credit.
Then, according to the condition of the problem, the debt should decrease by exactly x/24 (tenge) every month.
Table
Calculation of loan repayment by principal and by interest
|
No. of month (year) |
Principal payments |
Interest payments |
|---|---|---|
|
1 |  |  |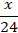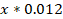
|
2 |  |  |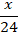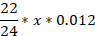
|
3 |  |  |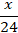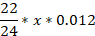
|
…………………………………………………………………………….. | ||
|
24 |  |  |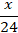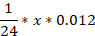
|
Total |
x |  |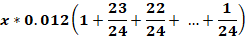
Let's make the equation: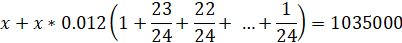 
Note that in brackets is the sum of the first n terms of the arithmetic progression:
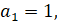
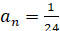
The formula for the sum of п members of an arithmetic progression:
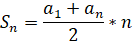
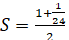* 24 = 
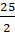, then
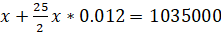
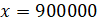
Result: 900 000 tenge was taken on credit.
In the article, we considered only two examples of problems, the solution of which is simplified using the formulas of arithmetic and geometric progressions, we think that this will help schoolchildren to overcome difficulties in solving economic problems from the bank.
As a result of the above material, it can be concluded that two completely different sciences, such as economics and mathematics, closely interact with each other. The actual application of mathematics in economic research, allowing you to explain the past, see the future and evaluate the result of your actions, will require significant effort, which is currently lacking in economics.
.png&w=640&q=75)
