Математическая модель процесса получения микрогранулированных оптических отбеливателей

Микрогранулированная выпускная форма белофора обладает следующими основными преимуществами по сравнению с традиционной (порошкообразной) выпускной формой:

• микрогранулированный продукт в массе обладает хорошей сыпучестью за счет снижения насыпного веса продукта;
• данная выпускная форма практически не подвержена слеживаемости;
• благодаря своей микропористой структуре продукт растворяется значительно быстрее, чем порошкообразный.

При получении микрогранулированного продукта на распылительной сушилке гидродинамические, тепло- массообменные процессы значительно усложняются сопутствующими процессами: разложением газообразующего вещества (ХГО – химический газообразователь), выделением газа из частицы распыленного раствора, образованием внутренней микропористой структуры (наподобие динамически изменяющейся пенной структуры).

При составлении математической модели можно ограничиться учетом удельного газовыделения, удельного расхода воды и интегральной химической кинетики разложения газообразующих веществ.

Разрабатываемое математическое описание процесса получения микрогранулированного белофора на распылительной сушилке из суспензий с добавкой порофора должно учитывать:

– кинетику формирования внутренней пористой структуры частицы за счет разложения вещества – газообразователя;

– изменение динамики движения частицы и кинетики тепло-массообменных процессов, связанное с изменением истинных размеров высыхающей капли и наличием большого количества пор в частице.

Математическое описание должно обеспечить взаимную связь между конструктивными, входными и выходными параметрами процесса.

Математическое описание должно включать в себя:

• уравнения гидродинамики (уравнения совместного движения частиц и газовой фазы);
• кинетику совместно протекающих процессов пенообразования (за счет разложения порофора) и пеноразрушения (данные зависимости необходимы для определения истинного размера капель и степени их пористости);
• уравнения кинетики сушки, с учетом того, что обычные тепло- массообменные процессы, характерные для процесса сушки распылением осложняются динамически изменяющимися размерами капель и количеством внутренних пор в пенном слое;
• зависимости материального баланса по частицам продукта и по газовой фазе;
• уравнения тепловых балансов также для частиц и газовой фазы.

К входным параметрам относятся:

• G_p – производительность по исходной суспензии, кг/ч;
• u₀ – начальное влагосодержание суспензии, кг/кг;
• с(u) – концентрация растворенных веществ в жидкой фазе суспензии, кг/кг;
• с_{го 0} – концентрация ХГО в суспензии в расчете на абсолютно сухой материал, кг/кг;
• Т₀ – начальная температура исходной суспензии, ⁰С;
• G_в – расход абсолютно сухого сушильного агента, кг/ч;
• Х₀ – начальное влагосодержание сушильного агента, кг/кг;
• Т_в0 – начальная температура сушильного агента ⁰С;
• Р – давление в сушилке абсолютное, Па;
• С_в – теплоемкость сушильного агента, Дж/(кг×⁰С);
• С_пар – теплоемкость влаги, содержащейся в воздухе, Дж/(кг×⁰С);
• С_вл – теплоемкость влаги, содержащейся в материале, Дж/(кг×⁰С).

Также должны учитываться физико-химические и тепло-физические свойства высушиваемого продукта и содержащегося в нем вещества – газообразователя:

• u_кр – критическое влагосодержание материала, кг/кг;
• u^* – равновесное влагосодержание материала, кг/кг;
• u_стр – влагосодержание частицы, при котором материал структурируется, кг/кг;
• n_p – кинематическая вязкость исходной суспензии, м²/с;
• s_р(u) – зависимость поверхностного натяжения материала от его влагосодержания, Н/м;
• r_вч(u) – зависимость плотности материала от его влагосодержания, кг/м³;
• a_п – параметр распределения пор в материале по размерам;
• С_тв – теплоемкость абсолютно сухого материала, Дж/(кг×⁰С);
• h_{вл го} – количество влаги, поглощенной при разложении 1 кг порофора, кг/кг;
• h_го – количество газа, выделившегося при разложении 1 кг порофора, кг/кг.

К входным конструктивным параметрам относятся:

• Д_диск – диаметр диска центробежного распылителя, м;
• n_диск – частота вращения диска, Гц;
• П – смоченный периметр диска, м.

Выходными параметрами математического описания являются:

• u_к – конечное влагосодержание продукта, кг/кг;
• Н_апп – высота сушильной камеры, м;
• Д_апп – диаметр цилиндрической части сушильной камеры, м;
• V_к – объем частиц высушенного материала, м³;
• m_к – масса высушенной частицы, кг;
• d_к – диаметр высушенной частицы, м;
• Т_в – конечная температура сушильного агента, ⁰С;
• Т – конечная температура высушенного материала, ⁰С;
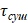• – полное время сушки, с.

Допущения, принятые при составлении математического описания процесса сушки белофора на распылительной сушилке из суспензии с добавкой порофора.

1. Влиянием добавки незначительных количеств ХГО в исходную суспензию продукта на изменение теплофизических характеристик частиц высушиваемого материала можно пренебречь.
2. Функцию распределения пузырьков по размерам в пузырьково-пенном слое частицы приближенно можно описать известной зависимостью, характерной для образования пористой структуры в полимерных пеноматериалах. При этом характер распределения в процессе сушки не изменяется.
3. Процесс непрерывной сушки распыленного материала может быть представлен в виде множества достаточно малых интервалов при движении частиц по высоте сушильной камеры с кусочно-постоянным изменением характеристик процессов на этих интервалах.
4. Кинетику сушки распыленного материала приближенно описываем традиционной моделью в виде двух последовательных периодов: 1-й период постоянной скорости сушки и 2-й период линейно убывающей скорости сушки.
5. Распыленные капли раствора имеют шарообразную форму.
6. Количество частиц при движении капель в сушильной камере остается постоянным, то есть не происходит агломерирования, слипания или дробления частиц, а на стенках камеры материал не накапливается.
7. По сечению высушиваемой капли (частицы) градиенты температуры и влагосодержания отсутствуют.
8. По диаметру камеры градиенты влагосодержания и температуры сушильного агента отсутствуют.
9. Гидродинамический режим движения сплошной и дисперсной фаз в сушильной камере – идеальное вытеснение.
10. Благодаря высокой интенсивности распыления дисперсии центробежными дисками фирмы «Ниро Атомайзер» полидисперсностью образующихся частиц можно пренебречь.
11. Тепловые потери от стенок камеры в окружающую среду учитываются отдельно.

Математическое описание химических процессов газовыделения за счет разложения вещества порофора (химического газообразователя), процессов пенообразования и пеноразрушения

Зависимость для определения массы капли (частицы) можно представить в следующем виде

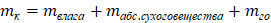 (1)

или с учетом принятых обозначений

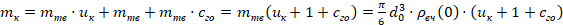(2)

Рассмотрим химическую реакцию разложения порофора (в данном случае в качестве ХГО используется карбамид).

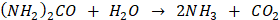.   (3)

Проведя необходимые расчеты, можно получить следующие данные

• при разложении 1 кг карбамида выделяется 1,3 кг или 1,12 м³ газов (h_го=1,3 кг/кг; h_Vго=1,12 м³/кг);
• приведенная плотность смеси газов r_газ=1,1607 кг/м³;
• на реакцию разложения затрачивается вода, содержащаяся в распыленных частицах; на разложение 1 кг карбамида необходимо 0,3 кг воды (h_{вл го}=0,3 кг/кг).

При условии, что смесь газов подчиняется законам идеального газа можно определить количество молей газа, содержащихся в 1 пузырьке пенного слоя  частицы

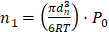,   (4)

где d_п – диаметр 1- го пузырька; Р₀ – давление в сушильном аппарате.

Частотная функция распределения растущих газовых пузырьков по размерам во вспениваемой композиции может быть описана следующей формулой [1]

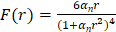,   (5)

где a_п – параметр распределения.

Таким образом, средний диаметр пузырька при данной функции распределения определяется как

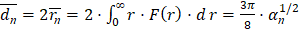. (6)

На основе допущения 2 используем формулы (5), (6) для определения среднего диаметра пузырька газа в капле высушиваемого белофора.

С учетом (6) из (4) можно получить

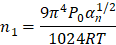 (7)

Скорость накопления газа в пенном слое частицы можно представить в виде

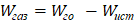,      (8)

где W_го, W_ист – соответственно массовые скорости выделения газа из порофора и истечения газа из пенного слоя частицы, кг/с.

По аналогии с д.у. изменения концентрации газа во вспенивающейся композиции [1-3] кинетика разложения порофора (карбамида) записывается в виде

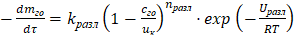,    (9)

где k_разл, n_разл, U_разл – константа скорости, порядок и энергия активации реакции разложения карбамида по уравнению (3).

Разложение карбамида начинается при определенной температуре –  Т_нп – температуре начала пенообразования (при Т< Т_нп k_разл = 0).

Изменение массовой скорости выделения газа в пенный слой частицы определяется выражением

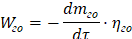   (10)

Процесс истечения газов из пенного слоя частицы выражаем в общем виде как

W_истеч = K_истеч ×DP× F,   (11)

где DP – перепад давлений, движущая сила процесса;

F – поверхность частицы;

K_истеч – коэффициент истечения, учитывающий все виды переноса выделяющейся парогазовой смеси через эту поверхность.

Перепад давлений считаем равным избыточному капиллярному давлению внутри пузырьков, которое выражается по Лапласу как .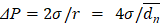

Скорость истечения газа из пенного слоя частицы можно определить по выражению

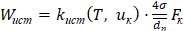,   (12)

где F_к = p d_к² – внешняя поверхность частицы, ;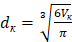

Текущий объем капли (частицы) определяется по формуле

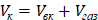, (13)

где V_вк – объем невспененного вещества частицы,

V_газ – количество накопленного газа в частице к моменту времени t, .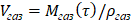

Массу накопленного газа в частице к моменту времени t можно вычислить, проинтегрировав выражение (8)

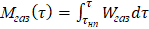,     (14)

где t_нп – время начала пенообразования от начала процесса (соответствует времени, когда температура частицы станет равной температуре начала пенообразования, т.е. Т=Т_нп).

Необходимое для расчета материальных и тепловых балансов количество пузырьков в капле сушимого материала вычисляется из зависимости

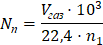    (15)

Выводы

Получены расчетные зависимости для определения геометрических размеров капли при использовании химического газообразователя.