В период трансформации системы тылового обеспечения (СТО) округа войск национальной гвардии (ВНГ), а также её адаптации и интеграции в общую систему снабжения Росгвардии становится актуальным поиск оптимального инструментария, необходимого для моделирования логистических процессов (ЛП) в ней, в том числе процесса заказа материальных средств (МС) потребляющему звену.
Именно от правильности выбора инструментария определяющего оптимальность процесса заказа МС будет зависеть эффективность управления запасами в целом, как с точки зрения затрат на их создание, так и с точки зрения удовлетворения потребности (отсутствия дефицита) всех потребителей рассматриваемой системы обеспечения.
С целью решения научной задачи, а также разрешения возникающих противоречий, в СТО округа ВНГ, необходимо определить оптимальный размер заказа необходимых МС, по средству определения минимальной его стоимости, с учетом производственных возможностей поставщиков и возможных ими недопоставок [3].
Инструментарием для решения поставленной задачи предлагается использовать региональный аукцион, который является аукционом единой цены, то есть каждый из предполагаемых поставщиков в этом регионе получает единую цену за поставляемые МС потребителям СТО округа.
В решении задачи предполагается, что рассматриваемый рынок является олигополистическим, где ценовые заявки участников определяют распределение поставок, текущие и региональные цены. В свою очередь, спрос предполагается рассматривать не зависящим от цены, то есть эластичность спроса, в данном случае, будет равна нулю. Сами ценовые заявки от производителей для всех аукционов одного торгового дня подаются одновременно перед его началом, где количество ступеней заявок не должно превышать заданного числа, а ценовые заявки используются на всех аукционах одного периода на протяжении данного торгового дня [1].
Региональные цены и объемы поставок определяются не только спросом на материальные средства и ценовыми заявками поставщиков (производителей), но и выбором их предполагаемых объемов, возможными потерями (недопоставками) и их производственными возможностями.
Целью каждого регионального аукциона является минимизация стоимости поставляемых МС конечному потребителю СТО округа ВНГ.
В рассматриваемой модели материальные потоки полагают, скалярными величинами и она упрощенно характеризует процессы в цепи поставок несимметричной функцией недопоставок, параметры которой периодически уточняют по экспериментальным данным, а разрывы градиентов и невыпуклость задачи существенно снижают эффективность алгоритмов, сводящих эту задачу к последовательному решению аппроксимирующих задач линейного программирования [2].
В свою очередь, задача линейного программирования – это метод решения экстремальной задачи на множествах n-мерного векторного пространства, задаваемая системой линейных уравнений и неравенств.
Сама же экстремальная задача является научным методом, состоящая в замене одних объектов на другие, в каком-то смысле близким к исходным, на более простые. Это, в свою очередь, позволит нам исследовать числовые характеристики и качественные свойства исследуемого объекта, сводя задачу к изучению более простых и более удобных объектов.
Цены и объемы поставок определяются ценовым заявкам производителя, где целью каждого проводимого аукциона (конкурса) является минимизация стоимости поставляемых МС (рисунок 1).
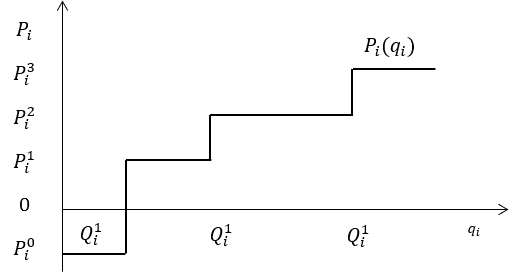
Рис. 1. Виды ценовых заявок поставщиков
В решаемой задаче рассматривается сеть из n взаимосвязанных поставщиков в региональной сети экономического кластера (рис. 2), где в период подготовки конкурсной документации отдел (оператор) получает следующую информацию, а именно:
- объединенную заявку на потребность в МС каждого из регионов (объектов) логистической системы , i=1,…,n;
- объединенную региональную ценовую заявку
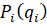всех поставщиков МС данного региона (объекта); - объемы МС в регионах (объектах)
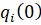; - объемы материальных потоков за предшествующий год
.
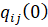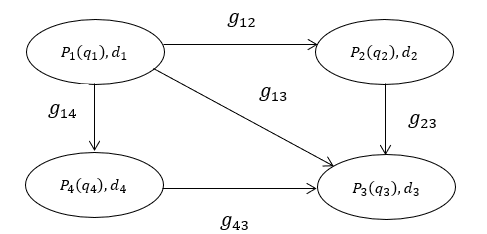
Рис. 2. Сеть экономического кластера [6]
Региональная ценовая заявка определяется как зависимость цены Pi от суммарного объема материальных средств (по номенклатуре), который предложен всеми поставщиками данного региона по цене, не превышающий Pi, так, что выполняется следующее равенство (1):
, 
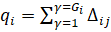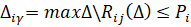(1)
Данное равенство дает возможность поставить в соответствие выбранному значению материальных средств, генерируемых поставщиками регионального рынка, объемы, закупаемые у каждого из них. Число региональных поставщиков заявку Gi, а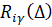 
– их ценовые заявки.
Функции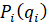 
являются непрерывными справа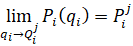 
На объемы региональных поставок наложены автономные ограничения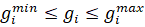 
. На межрегиональные объемы поставок 
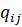из i-го в j-й регион также наложены ограничения, такие как: 
.
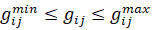Вводимые ограничения дают возможность учитывать, как технологические возможности поставщиков по выпуску, так и их динамические возможности по скорости изменения объемов поставок материальных средств, где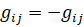 
.
Предполагается, что передача объема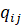 
из i-го в j-й региональный рынок связана с возможными недопоставками материальных средств, а эти потери могут быть охарактеризованы непрерывной монотонно возрастающей функцией 
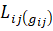, для которой справедливы соотношения:
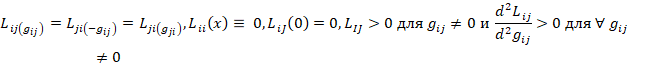
Характер зависимости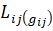 
от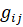 
представлен на рисунке 3.
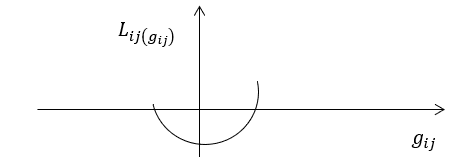
Рис. 3. Зависимость возможных недопоставок
Потери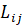 
делятся между соответствующими региональными рынками в заданном соотношении и создают дополнительный спрос на материальные средства 
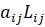в i-м регионе и 
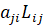в i-м регионе, где 
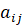константы, 
.
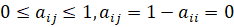Баланс необходимых материальных средств в логистической системе характеризует уравнение 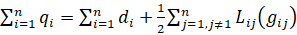(2):
(2)
где: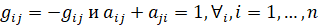 
Баланс логистической системы выполняется, если выполнены региональные балансы 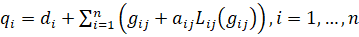(3):
(3)
Наряду с объединенной ценовой заявкой поставщиков i-го рынка введем объединенную стоимостную заявку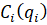 
, как зависимость стоимости материальных средств всех возможных поставщиков от ее объема.
Тогда стоимость генерации на i-м рынке можно будет описать следующим соотношением 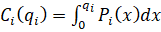(4):
(4)
Для непрерывной ценовой заявки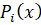 
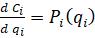(5):
(5)
Так как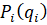 
– монотонные, кусочно-постоянные неубывающие функции, непрерывные справа, то 
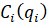являются выпуклыми, кусочно-линейными, их производная в точке излома равна ее большему значению, а, следовательно, аналогичная стоимостная заявка может быть рассмотрена для каждого поставщика на региональном рынке.
Тогда общая стоимость генерации всеми поставщиками материальных средств на рынке будет определена как 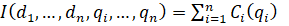(6):
(6)
Распределение поставок будет оптимальным и соответствовать минимуму, в случае выполнения условий целевой функции I по 
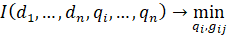, где (7):
(7)
с учетом ограничений, таких как (8, 9):
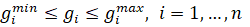(8)
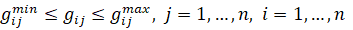(9)
и балансов, рассмотренных ранее, где последние отношения включают нелинейные функции, что приводит к невыпуклости решаемой задачи оптимального распределения поставок для одного периода.
Далее определи составляющие ее решения, как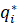 
, 
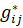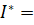
, а минимум ее целевой функции, как минимальную общую стоимость поставки 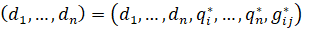(10):
(10)
где стоимость поставки I и ее минимальная величина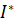 
зависят не только от 
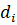, но и от ценовых заявок 
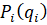, а также от предаукционного состояния рынка – текущих значений 
, 
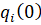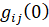(через автономные ограничения, наложенные на 
, 
).
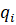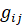Неизвестными величинами в задаче оптимального распределения поставок (3, 7, 8, 9) являются региональные объемы поставок и объемы межрегиональных потоков.
Если в рыночной региональной сети все поставщики связаны между собой, то общее число неизвестных задач будет равно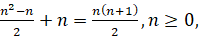 
где первое слагаемое этого выражения соответствует числу потоков 
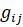, а второе – числу региональных поставщиков.
Поскольку эти переменные должны удовлетворять n уравнениям баланса (3), то число свободных переменных в задаче оптимального распределения поставок равно числу межрегиональных материальных потоков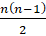 
для рассматриваемой логистической сети, где все поставщики в рыночной региональной сети взаимно связаны.
Следовательно, еcли n = 1, то получается единственная свободная переменная для n = 3 – три и так далее.
Рассматривая необходимые условия оптимальности, исключив по условиям (3) региональные объемы поставок материальных средств задачу оптимального распределения поставок (3, 7, 8, 9) можно записать как задачу нелинейного программирования, а именно (3):
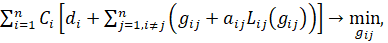(11)
при выполнении следующих неравенств:
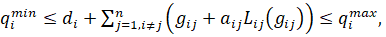(12)
и автономных ограничений:
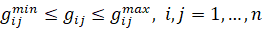(13)
Объемы межрегионального обмена материальными средствами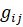 
будут являться независимые переменные решаемой задачи 
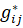, а региональные поставки материальных средств рассчитываться из уравнений баланса (13) и такое решение является вектор - функций от вектора потребления 
.
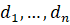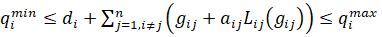(14)
и
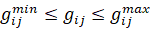(15)
Допустим, что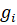 
– точки, где функция 
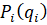непрерывны. Тогда из условий стационарности I по 
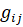получаем для двух взаимосвязанных регионов:
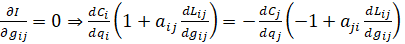(16)
Здесь принято во внимание, что с учетом (2.21) получаем (2.34):
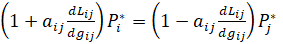(17)
Здесь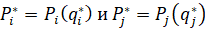 
– цены, соответствующие выбранным суммарным объемам поставок в ценовых заявках для регионов i и j соответственно.
Назовем в этих уравнения величины, стоящие в левой и правой частях равенства (17), скорректированными ценами в одном регионе относительно другого, где для i-го региона по отношению к j-му это будет 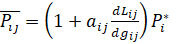(18):
(18)
а для j-го по отношению к i-му соответственно 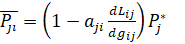(19):
(19)
Следовательно, потоки между двумя регионами в режиме, который соответствует неактивным автономным ограничениям и участкам непрерывности функций ценовых заявок, могут быть оптимальны в том и только том случае, если скорректированные цены в этих регионах равны 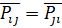(20):
(20)
Далее проведем анализ, где гарантированно не улучшение целевой функции I путем вариации межрегиональных потоков МС, приводит к следующим общим условиям оптимальности решения задачи (11 - 13) при следующих ограничениях (21, 22):
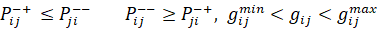(21)
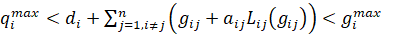(22)
где левый и правый пределы ценовых показателей будут описываться как: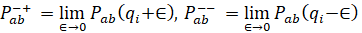 
Далее необходимо рассмотреть условия оптимальности для случая активных автономных ограничений.
Если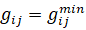 
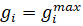или 
или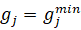 
, то допустимы только отрицательные изменения 
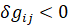и рассматриваемые условия неулучшаемости I при таких изменениях будут иметь вид 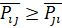(23):
23)
Аналогично, если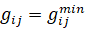 
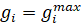или 
или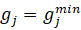 
, то распределение является оптимальным только в случае, когда 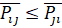(24):
(24)
В свою очередь, это позволяет нам утверждать и сделать вывод о том, что, если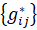 
оптимальное решение задачи (11 - 13), то выполнены следующие условия, а именно – это нестрогие двухсторонние ограничения 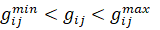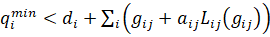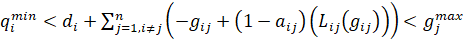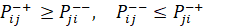(25):
,
,
,
(25)
Ограничения на потоки 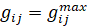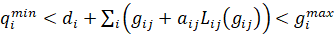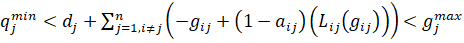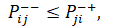(26):
,
,
,
(26)
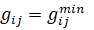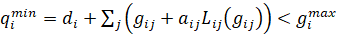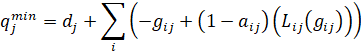
или 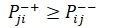(27):
,
,
(27)
Строгие ограничения – вариант один (28):
, 
,
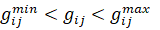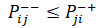
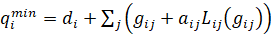или
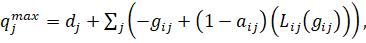(28)
или вариант два (29):
, 
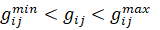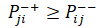
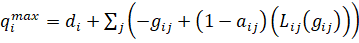
или
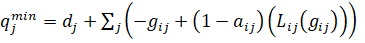(29)
С целью выявления межрегиональных условий оптимальности необходимо рассмотреть линейную часть логистической сети, состоящую из трех региональных рынков.
Допустим, что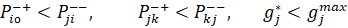 
, тогда материальный поток направлен из i-го в j-й и далее в k-й рынок.
Автономные ограничения на объем генерации на i-м рынке активно, что исключает увеличение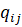 
. Однако две одновременно положительные вариации 
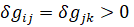допустимы.
Проведенный выше анализ предполагает, что фрагмент рассматриваемой сети, состоящий из двух региональных рынков, приводит к следующим условиям оптимальности для участков непрерывности функци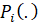й 
при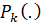 
и при неактивных ограничениях 
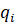и 
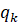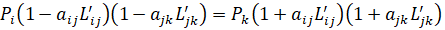(30):
(30)
и к общим условиям оптимальности для точек скачкообразного изменения цены на функциях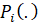 
и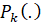 
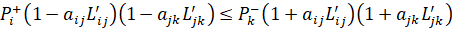
, а именно 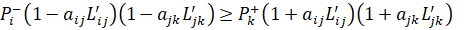(31):
(31)
Для активных автономных ограничений эти локальные условия оптимальности имеют тот же вид, что и условия оптимальности для двухрегиональной системы, полученные выше. Однако в этих условиях фигурируют многорегиональные приведенные цены, которые определены левыми и правыми частями равенства (30), вместо локальных приведенных цен (18). Эти условия устанавливают, что в задаче об оптимальном распределении два региональных рынка, связанных между собой в сети через несколько региональных рынков с активными ограничениями на генерирование, могут иметь различные многорегиональные приведенные цены только в том случае, если, по меньшей мере, один из потоков между ними либо объем генерации на одном из рынков вышел на активное ограничение [4].
В свою очередь, определяя проблему глобального минимума в задаче оптимального распределения поставок одной из главных особенностей задачи оптимального распределения поставок (3, 7, 8, 9) является невыпуклость ее целевой функции, где каждая из стоимостных заявок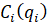 
по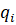 
становится 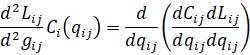(32):
(32)
В силу линейности стоимостной заявки первый сомножитель под знаком производной постоянен, а его знак совпадает со знаком ценовой заявки.
Таким образом, знак второй производной совпадает со знаком ценовой заявки, так как функция потерь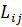 
строго выпукла. Из-за возможного наличия отрицательных ступеней в функциях ценовых заявок функции 
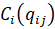невыпуклы и задача становится многоэкстремальной.
Следовательно, при использовании полученных выше необходимых условий оптимальности или при использовании прямого поиска минимума стоимости поставки из произвольного начального приближения не гарантируется определение глобального минимума целевой функции. В этих случаях необходимо проверять, является ли полученное решение глобальным или локальным экстремумом, и если минимум оказывается локальным, то, сильно ли он отличается от глобального и какое улучшение целевой функции в единицах поставки возможно при дальнейшем продолжении поиска [5].
Рассмотрим расширение задачи оптимального распределения (3, 7, 8, 9) за счет исключения автономных ограничений (9) и уравнений связи (3), где далее она приобретает вид (33):
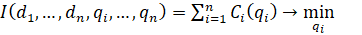(34)
при соблюдении условий 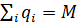(34):
(34)
c ограничениями 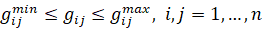(35):
(35)
где: M – параметр, равный суммарным недопоставкам МС при межрегиональных передачах, где наложены следующие ограничения 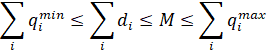(36):
(36)
Введем в рассмотрение функцию Беллмана, используя следующее рекуррентное соотношение (37):
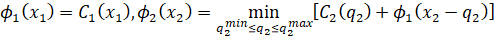, (37)
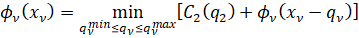
и соотношение 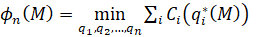(38):
(38)
позволяющие определить глобальный минимум целевой функции и соответствующие ему потери в цепях поставок, отвечающие уравнению 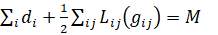(39):
(39)
Полученное решение определяет нижнюю достижимую границу стоимости поставки для заданных потерь в логистической цепи.
Следовательно, на основе выше полученных условий оптимальности рассчитано оптимальное решение и получены значения *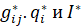
, где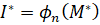 
. В этом случае соотношение (39) позволяют рассчитать 
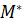и затем решить задачу (33, 34, 35), для полученного результата – M*.
Если величина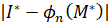 
является достаточно малой, то можно закончить поиск и рассматривать полученный глобальный минимум – 
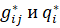, как удовлетворительное решение поставленной научной задачи.
Новизна разработанной модели заключается в том, что полученные выше условия оптимальности могут быть использованы для синтеза автоматических систем управления поставок, где периодическую последовательность закупки можно заменить одним непрерывным аукционом.
Решение научной задачи позволило создать целостную «картину», характеризующую процесс заказа МС, а также совершенствовать механизм формирования заявок и оптимизации закупочной деятельности, централизованных поставок для нужд войск округа ВНГ, в целях экономии государственных средств, выделяемых в интересах Росгвардии.
.png&w=640&q=75)
