В настоящее время из всех возможных видов безопорного движения реализовано лишь одно – реактивное, с опорой на газовую струю, сформированную внутри движущегося объекта, теоретическое обоснование которого было предложено Э.К. Циолковским в 1903 г. Все остальные формы безопорного движения рассматриваются научным сообществом, как противоречащие фундаментальным основам механики.
Анализ творчества Циолковского, даёт основание утверждать, что ещё в возрасте шестнадцати лет, в 1873 г., он рассматривал альтернативный способ безопорного движения, предполагая использовать для этого два перевернутых маятника, машущих синхронно, во встречных направлениях.
В 1899 г. предложенную Циолковским идею пытался разрабатывать американский инженер Р.Х. Годдард, но вскоре, как и Циолковский, переключился на анализ реактивного движения. Он был одним из пионеров современной ракетной техники, создал первый жидкостный ракетный двигатель.
Первые теоретические выводы свойств обратного маятника были опубликованы в 1908 г. манчестерским математиком А. Стефенсоном.
Динамическая стабилизация обратного маятника подробно изучалась академиком П.Л. Капицей в 1951 году. Экспериментальное устройство с кривошипным приводом, построенное специально для данных экспериментов, получило название «маятник Капицы». Особенностью маятника Капицы является то, что перевернутое (вертикальное) положение маятника может быть устойчивым, в случае быстрых вибраций подвеса.
В последующем это направление безопорных движителей не получило своего развития.
Таким образом, первые робкие попытки реализовать безопорное движение закончились неудачей, фактически, из-за недостаточной подъёмной силы, способной развивать обратным маятником. Эта неудача лишь утвердила уверенность научного сообщества в том, что такое движение не может быть реализовано в принципе, так как в этом случае оно нарушает Третий закон Ньютона, который гласит, что каждому действию соответствует равное и противоположно направленное противодействие, сформулированный Ньютоном в 1686 году.
В классической трактовке Третий закон Ньютона гласит, что векторная сумма всех внутренних сил замкнутой механической системы равна нулю.
Первой причиной заблуждения стало слияние таких понятий как замкнутая и закрытая системы. Традиционно сложилось представление о тождественности этих определений, в то время как они принципиально различны.
Замкнутая система – это теоретическая абстракция, дающее представление о распределении векторных сил внутри системы, которая характеризуется таким понятием как «Главный вектор» механической системы. Если «Главный вектор» равен нулю, то такая система всегда будет находится в состоянии покоя, и она не может участвовать ни в каком самостоятельном движении. Если «Главный вектор» отличен от нуля, то механическая система выходит из равновесного состоянии и самостоятельно двигается относительно внешней среды.
Закрытая система – это проектно-конструктивный термин, описывающий конструкцию, которая не имеет тех или иных механизмов для взаимодействия с внешней средой для формирования собственного движения, например, гребной и воздушный винты, парус, колеса и так далее.
Таким образом, для анализа теоретической возможности реализации безопорного движения, надо четко разделять такие понятия как замкнутая механическая система (теоретически абстрактное) и закрытая механическая система (конструктивно конкретное).
Если в закрытой механической системе «Главный вектор» равен нолю, то такая система ни при каких обстоятельствах не сможет реализовать самостоятельное безопорное движение. Но если в замкнутой механической системе «Главный вектор» будет отличен от нуля, то такая система сможет реализовать собственное движение без опоры на внешнюю среду. Именно эта ситуация рассматривалась исследователями применительно к обратному маятнику.
Основные этапы практического освоения безопорного движения рассмотрены в работе «Безопорное движение: миф или реальность» [1].
Среди исследователей безопорного движения особо следует отметить, основоположника практического безопорного движения В.Н. Толчина [1], который в 1967 году представил свою модель безопорного движителя (рис.1) на обсуждение специалистов физического факультета Пермского государственного университета. Мнения специалистов разделились на прямо противоположные. Одни видели в этой конструкции «светлое» будущее безопорного движения, другие безграмотность и нелепость самого автора, замахнувшегося на святое классической физики – Третий закон Ньютона.

Рис. 1. Модель безопорного движителя В.Н. Толчина
Толчин, столкнувшись с реальностью безопорного движения, я полагаю, был удивлён не меньше других, но, несмотря на это, быстро перешёл от опытов с крутильными весами к модели с поступательным движением. К сожалению, он был прекрасный конструктор-практик, но не владел основами теоретической механики. С другой стороны, как и сегодня, в прошлом веке существовало заблуждение относительно вращательного движения, поэтому в своей книге «Инерцоид» Толчин писал [3, с. 85]:
«Центростремительные и центробежные силы не возникают раздельно, они всегда уравновешивают друг друга. Их равнодействующая всегда равна нулю. Спрашивается, как можно этот физический нуль разлагать на горизонтальную и вертикальную слагающие?
Тем не менее, в целом ряде работ говорится о действии неуравновешенных центробежных сил. Многие стараются использовать «действие» центробежных сил для осуществления всевозможных, порою очень «хитрых», центробежных движителей, для «небесного лифта», для вывода космического корабля без применения ракеты и т.п.»
Как видим, Толчин, сделав модель, движущей силой которой выступала центробежная сила, природу этой силы не знал, поэтому так до конца и не понял, за счёт чего получился наблюдаемый им эффект безопорного движения. Не понял не только он, но и специалисты по теоретической механике, которые воочию видели эту модель, одного взгляда на которую было достаточно, чтобы понять какой физический принцип заставляет её двигаться. Толчину не хватило всего полшага, чтобы создать действующую модель безопорного движителя способного преодолеть гравитацию.
Ошибка Толчина в понимании природы вращательного движения отражает второй аспект общего заблуждения невозможности реализации безопорного движения, в основе которого лежит ошибка Ньютона в понимании центростремительной силы.
Отрывая свой труд «Материалистические начала натуральной философии» 1686 года Исаак Ньютон предваряет его описанием терминов, которые он использует в своей работе [2, с. 26]:
«Центростремительная сила есть та, с которою тела к некоторой точке, как центру, отовсюду притягиваются, гонятся или как бы то ни было стремятся. Такова сила тяжести, под действием которой тела стремятся к центру Земли; магнитная сила, которою железо притягивается к магниту, и та сила, каковою бы она не была, которые планеты постоянно отклоняются от прямолинейного движения и вынуждаются обращаться по кривым линиям…».
Здесь Ньютон достаточно недвусмысленно определяет центростремительную силу, как некую внешнюю силу, действующую на тела и заставляющую их изменять свое прямолинейное движение, в соответствии с его первым законом механики, на криволинейное движение. Здесь важно отметить, что под центростремительной силой Ньютон понимает именно силу, а не просто препятствие прямолинейному движению.
Но вот то, что он пишет далее является одной из его фундаментальных ошибок, определившей судьбу центробежной силы [2, с. 26]:
«Камень, вращаемый в праще, стремится удалиться от вращающей пращу руки, и этим свои стремлением натягивает пращу тем сильнее, чем сильнее вращение, и как только его пустят, то камень улетает. Силу, противоположную сказанному стремлению, которою праща постоянно оттягивает камень к руке и удерживает его на круге, т.е. силу, направленную к руке или к центру описываемого круга, я называю центростремительной. Это относится и до всякого тела, движущегося по кругу.»
Здесь Ньютон становится заложником логического принципа «аналогия»: если гравитационная и магнитная сила являются центростремительными, то и любое непрерывное ограничение прямолинейного движения является силой.
Если в отношении гравитационной и магнитной силы утверждение, что эти силы являются центростремительными, при определенных условиях, верно, то распространение этого утверждения на все случаи непрерывного ограничения прямолинейного движения является фундаментальной ошибкой Ньютона. Праща, удерживающая камень на орбите вращения, не создает никакой силы, а лишь препятствует прямолинейному движению камня. Это доказывается тем, что сила, которая натягивает пращу, пропорциональна угловой скорости вращения, и если бы существовала аналогичная центростремительная сила, то тело бы, сколько не увеличивай скорость вращения, всегда оставалось бы в равновесии, так как пропорционально этому увеличивалась бы и центростремительная сила. Но при достижении определенной скорости вращения, если прочность материала пращи будет недостаточна, он рвется и камень уходит с орбиты, но не в сторону центра, а в противоположную. Причём не по касательной, как многие считают, а под углом к ней в 54,74 градуса.
Если бы Ньютон, провел опыт с телом, свободно передвигающимся по вращающемуся штоку, то увидел бы, что тело это, всегда стремится от центра к периферии, и никогда обратно. Если не ограничивать тело на внешнем конце штока, то оно всегда уходит с орбиты вращения. Это указывает на то, что на тело во время вращения действует, лишь одна сила, направленная в противоположную от центра вращения сторону, а центростремительной силы в пассивных связях физически не существует. Поэтому отождествлять реакцию кинематической связи с центростремительной силой в корне не верно.
Сделав эту фундаментальную ошибку, Ньютон вновь возвращается к рассмотрению центростремительной силы тождественной гравитационному и магнитному взаимодействию, тем самым дав понять, что кинематическая связь во вращательном движении и собственно источники центростремительной силы суть одно и тоже, закрепив в сознании своих последователей искаженное понимание природы центростремительной силы. Так он пишет в отношении тела, вращающегося внутри круга [2, с. 81]:
«Такова центробежная сила, с которою тело давит на круг; ей равна и противоположна сила, с которою круг отталкивает тело к своему центру».
Здесь мы уже видим приложение четвертого следствия Третьего закона Ньютона: у любого действия есть равное и обратно направленное противодействие. В рассмотренном случае в отсутствии природной центростремительной силы (гравитационной, магнитной или иной аналогичной) круг лишь ограничивает движение тела под действием центробежной силы, но сам при этом никакой силы не создает.
Далее Ньютон достаточно витиевато объясняет, что основной причиной, по которой Луна находится на своей орбите, есть равенство центростремительной и центробежной сил [2, с. 513]. Причем в качестве центростремительной силы Ньютон рассматривает силу тяжести, или как мы её теперь называем силу гравитационного взаимодействия.
Этим утверждением Ньютон фактически признает, что при наличии двух равных по модулю и противоположных по направлению сил вращательного движения, тело находится в равновесии неограниченно долго. Поэтому если в связке двух тел отсутствует какая-либо природная центростремительная сила, то тело-сателлит, которое движется вокруг центра вращения, будет находиться под действием всего одной физически реальной силы - центробежной. В связи с этим для того, чтобы удержать его на стационарной орбите нужна кинематическая связь, позволяющая сохранять расстояние между телами постоянным. При этом следует помнить, что эта связь, также как и тело-сателлит будет находиться под воздействием центробежной силы со всеми вытекающими из этого последствиями.
Таким образом, вращательное (криволинейное) движение является уравновешенным в двух совершенно разных случаях:
- В качестве центростремительной силы выступает некая природная сила, характер которой не зависит от скорости движения тела-сателлита по криволинейной траектории. В качестве такой силы может выступать гравитационная, магнитная или аналогичная им сила.
- Вращательное (криволинейное) движение осуществляется исключительно под воздействием центробежной силы, действие которой ограничивается кинематической связью, которая в свою очередь, так же находится под её воздействием. В этом случае, никакой центростремительной силы в криволинейном движении нет.
Это принципиальное различие в понимании центростремительной силы. К сожалению, как и в отношении закрытой и замкнутой механических систем, так в отношении центростремительной силы существует серьёзное заблуждение, основанное на непонимании разницы между собственно силой и реакций на силу. Это непонимание, и привело Ньютона, и последующие поколения учёных, к неверному отождествлению понятия центростремительной силы, вызванной гравитационным воздействием с реакцией элементов конструкции, которая фактически является репликой центробежной силы, в то время как собственно центростремительная сила не зависит от скорости движения тела-сателлита.
Основываясь на понимании двух основных заблуждений относительно безопорного движения, и конструктивных решениях Толчина, можно сформулировать основные требования к конструкции безопорного движителя, способного перемещать любые объекты без какой-либо опоры на внешнюю среду.
На рисунке 2 представлена принципиальная схема безопорного движителя, основанная на принципе некомпенсированной центробежной силы.
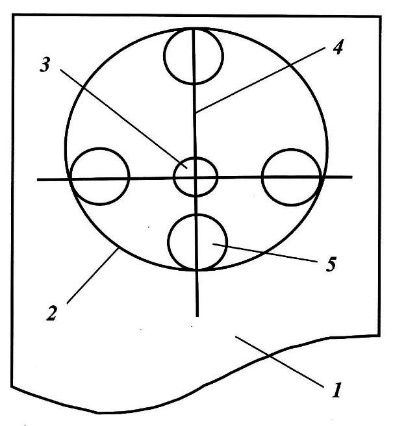
Рис. 2. Принципиальная схема безопорного движителя
В описании принципиальной схемы используются следующие термины и определения:
Дебаланс – некомпенсированная центробежная сила; разница между центробежными силами двух тягал расположенных на прямой линии с разных сторон от оси их вращения; линейное тяговое усилие.
Дисбаланс - эксцентриситет орбиты тягал; расстояние между геометрическим центром обечайки и центром вращения тягал.
Обечайка - кольцо, ограничивающее движение тягал и удерживающее их на заданной орбите.
Тягало – груз, создающий центробежную силу при вращении внутри обечайки.
Шток - стержень, обеспечивающий вращательное движение тягало внутри обечайки.
На корпусе устройства (рис. 2 п.1) методом жёсткого крепления устанавливается обечайка (рис. 2 п.2). На корпусе также крепится вал (не показан) с возможностью свободного вращения вокруг собственной оси, передающий вращательный момент от двигателя к исполнительным элементам устройства. На вал жестко крепится держатель (рис. 2 п.3), который удерживает штоки (рис. 2 п.4). На штоках устанавливаются тягала (рис. 2 п.5), таким образом, чтобы те могли свободно перемещаться по ним внутри обечайки.
Геометрический центр обечайки смещён относительно центра вращения держателя штоков на величину, определяющую дисбаланс конструкции. Профиль обечайки по траектории движения тягал может быть выполнен как в виде круга, так и в виде эллипса, или иного сложного профиля.
При передаче вращательного движения от двигателя на вал, а через него на держатель штоков последние приводятся во вращение, обеспечивая при этом вращательное движение установленным на них тягалам. Тягала под действием центробежной силы, возникающей при вращательном движении, начинают двигаться в сторону обечайки, до тех пор, пока не упрутся в неё. При увеличении скорости вращательного движения тягала, ограниченные в своём перемещении обечайкой, начинают оказывать на неё давление, сила которого передается на корпус конструкции.
Благодаря тому, что геометрический центр обечайки смещён относительно центра вращения тягал, который совпадает с центром вращения держателя штоков, в конструкции существует направление, при котором тягала максимально удаляются от своего центра вращения с одной стороны и максимально приближаются к этому центру с противоположной стороны, создавая центробежный дебаланс, который всегда направлен в сторону максимального удаления тягал от центра вращения.
В точке максимального удаления тягал от центра вращения создаётся некомпенсированная центробежная сила, которая, воздействуя на обечайку, передаёт корпусу устройства линейное тяговое усилие, приводя его в движение в заданном направлении.
В качестве теоретического обоснования работоспособности рассматриваемого устройства используются известные законы механики вращательного движения. Известна зависимость центробежной силы от параметров вращательного движения [2]:
Fцб = m*ω2*R, (1) где
Fцб – центробежная сила (Н);
m – масса, вращающегося на орбите тела (кг);
ω – угловая скорость вращения (рад/с);
R – радиус вращения тела (м).
Если два тела с одинаковой массой находятся на одной радиальной прямой с противоположных сторон от центра вращения, то дебаланс этой пары определяется как разница между их центробежными силами:
Dцб = dFцб = m*ω2*dR, (2) где
Dцб – дебаланс (Н);
dFцб - разница центробежных сил двух тягал, по направлению дисбаланса конструкции (Н);
dR – дисбаланс конструкции (м).

Рис. 3. Демонстрация безопорного движения
Если, например, частота вращения тягал массой по 0,1 кг каждое равна 314 рад/с (3000 об/мин), а дисбаланс 0,2 м, то, центробежный безопорный движитель создаст дебаланс:
Dцб = 0,1 * 3142 * 0,2 = 1972 Н = 201 кгс
Иными словами, одно тягало массой в 100 грамм, будет создавать линейное тяговое усилие в 200 кгс, обеспечивая взлётный вес транспортного средства до 190 кгс в случае установки на нем рассмотренного устройства.
Для того, чтобы устранить «паразитные» движения, возникающие при вращении, тягал, в конструкции реального устройства необходимо использовать два рабочих модуля, расположенных на одной оси, с вращающимися в противоположные стороны тягалами, что позволит обеспечить полную компенсацию «паразитных» движений и удвоить тяговую силу в заданном направлении.
Таким образом, укоренившееся заблуждение в отношении невозможности реализации безопорного движения основывается на двух фундаментальных заблуждениях:
- Отождествление абстрактно-теоретического понятия «замкнутая механическая система» с проектно-конструктивным понятием «закрытая механическая система».
- Отождествление понятия «центростремительная сила» с «реакцией опоры» в направлении центра вращения.
Устранение этих понятийных противоречий позволяет реализовывать принцип безопорного движения, продемонстрированный в моделях Точилина, в том числе и на объектах способных перемещаться в пространстве без какой-либо опоры на внешнюю среду в вертикальном направлении.
[1] В 1936 году Владимир Николаевич Толчин, будучи конструктором Пермского машиностроительного завода им. Ф.Э. Дзержинского, изобрёл и с моделировал первое в нашей стране, а возможно и в мире, устройство способное перемещаться с помощью безопорного движителя, названное им, не совсем удачно, – инерцоид
[2] Эффект безопорного движения демонстрирует цепочка металлических шариков. На рисунке 3 видно, как цепочка самостоятельно поднимается в верх под действием центробежной силы.

.png&w=640&q=75)