Повышение точности МНК в решении навигационных задач

При решении радионавигационной задачи используется дальномерный метод, основанный на измерениях псевдодальности (R_i) между i-ым навигационным космическим аппаратом (НКА) и навигационным приемником. Для повышения точности решения используется весовой МНК, причем выбор весов является предметом исследований [1, 2]. В частности, для устранения аномальных выбросов псевдодальности до отдельных НКА путем коррекции соответствующих весов используется метод RAIM [2]. Целью статьи является исследование влияния весовой обработки в методе RAIM на точность решения навигационной задачи.

Номинальные псевдодальности P_i приемника до НКА определяются по формуле:

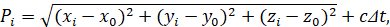    (1)

где x_i, y_i, z_i – координаты i-го НКА, x₀, y₀, z₀ – номинальные координаты навигационного приемника, c – скорость света, Δt – разница шкал времени навигационной системы и приемника.

Весовой МНК описывается выражением [3]:

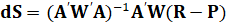,     (2)

где A – матрица направляющих косинусов, P – вектор-столбец номинальных псевдодальностей, R – вектор-столбец измеренных псевдодальностей, W – весовая матрица.

Весовая матрица W определяется следующим образом:

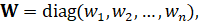    (3)

где diag – функция, формирующая диагональную матрицу с элементами на главной диагонали.

Отношение С/N₀ несущей к шуму является ключевым параметром при анализе характеристик навигационных приёмников. Данная модель в основном применяется для уменьшения эффекта многолучевого распространения и описывает дисперсию 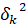 фазы несущей как функцию от С/N₀:

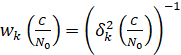,    (4)

где k=1, 2, …, n – номер спутника, n – максимальное количество спутников.

Данный метод справедлив при известных значениях С/N₀. Когда эти значения определить невозможно, есть возможность корректировать веса при помощи метода автономного контроля целостности RAIM. В данном методе псевдодальность представляется как линейная функция поправок к координатам текущего местоположения. Невязку r псевдодальностей можно найти как разницу между линеаризованными измерениями (разница между измеренными R и номинальным P значениями псевдодальности):

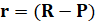.    (5)

Нормированный остаток v может быть сформирован:

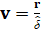,    (6)

где 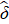 – оценка вектора усредненной дисперсии [2]:

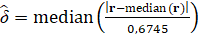,     (7)

где median – функция, определяющая медианное значение массива.

Существует более 10 видов счетных функций оценки. Для эксперимента рассмотрим счетную функцию d Коши [2]:

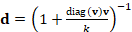,    (8)

где k=2,3849 – постоянный параметр.

Уточненная счетной функцией d матрица 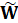 весов, используемая в дальнейшем в МНК (2), рассчитывается следующим образом:

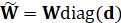.    (9)

Алгоритм, описанный выражениями (2) и (9), реализован программно. На рисунке представлена градиентная траектория, а также показано положение спутников относительно навигационного приемника (точками обозначены спутники, а приемник – крестом).

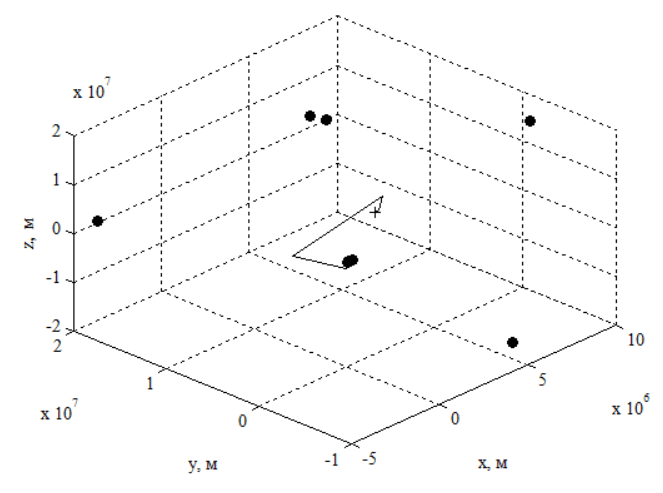
Рис. Градиентная траектория сходимости алгоритма

Оценка координат с помощью разработанного алгоритма сходится к истинному значению.

Произведён сравнительный анализ точности алгоритма с весовой и без весовой обработок, а также весовой обработки с коррекцией функцией Коши. Результаты измерений приведены ниже (табл. 1). Проведены 7 серий, по 2000 экспериментов с использованием следующей модели внесения нестабильностей расстояний:

R=R+dr,    (10)

где dr – вектор нестабильности расстояний.

Для каждой серии вектор нестабильности задавался отдельно и не менялся на протяжении всей серии.

Таблица 1

Сравнение эффективности МНК

Весовой метод обработки данных дает меньшее СКО оценки координат приемника, чем обработка без весов. Средний выигрыш взвешенного МНК ∆₁ составляет около ∆₁=10,6 % относительно обычного МНК. При дополнительной коррекции весовых коэффициентов функцией Коши средний выигрыш в уменьшении СКО ∆₂ составляет около ∆₂=12,5 %.

Исследована возможность МНК с дополнительной коррекцией противостоять искажениям параметров единичных спутников. Для этого в выражении (10) варьированы геометрические расстояния отдельных спутников. Результаты эксперимента представлены в таблице (табл. 2).

Таблица 2

Зависимость СКО от количества спутников с вариациями геометрических расстояний

Видно, что взвешенный МНК с коррекцией имеет явное преимущество, которое в среднем составляет 11,5 %. Лучше всего алгоритм с коррекцией проявляет себя при устранении единичной ошибки (выигрыш около 20 %). При увеличении числа спутников с искаженной псевдодальностью эффективность алгоритма с дополнительной коррекцией снижается.