Неизвестными параметрами пласта служат такие параметры, как давление в пласте рпл, χ=µβk*– пьезопроводимость, K=kµh - гидропроводимость. Однако, учитывая специфику вопроса, вместо пьезопроводимости следует рассмотреть величину χ/rс2, так как в эту величину входит еще одна неизвестная величина как параметр rc – эффективный радиус скважины (с учетом скин-эффекта).
Если неизвестно, что происходит после остановки скважины - выход (приток) или поток притока, то есть поток, который возникает в результате резкого (внезапного) перехода потока от одной постоянной к другой, тогда вместо одного параметра нужно взять параметр притока α.
Формула 1 представляет собой анализ кривой изменения давления (КИД) при постоянной мощности.
Давайте сначала рассмотрим более простую ситуацию, то есть до того, как скважина будет введена в эксплуатацию. Пусть ее выход (в пластовых условиях) будет постоянным Q0 после спуска скважины. Тогда мы получим поэтому давление в скважине уменьшается на кривой возврата давления (КИД) (см. уравнение (8)):
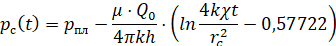 (1)
(1)
Таким образом, если:
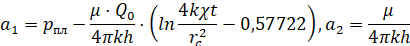 (2)
(2)
ввести функции и параметры,
x1 (t) ≡ 1, x 2 (t) = −Q0 ⋅ ln t (3)
то уравнение (1) можно записать в следующем виде:
pc (t) = a1 x1 (t) + a2 x 2 (t)
На практике точное значение давлений pc(ti) дается с его приблизительными значениями y(ti)=pc(ti)+εi которые измеряются с некоторой погрешностью. В нем коэффициенты â1 и â2 основанные на методе наименьших квадратов, также будут отличаться от точных значений этих параметров (2). Размер этих различий характеризуется погрешностями μj. На рисунках 1a-1b гистограммы распределения параметров a1 (рис. 1a) и a2 (рис.1b), которые представляют это, построены для 1000 видов. Таким образом, измеренные значения моделируются на основе уравнения y(t) = pc(ti) + εi.
Уравнение (1) было рассчитано по уравнению, но погрешности εi равномерно распределены и моделируются нелинейно. Были получены следующие значения параметров для расчета: χ3 = 1000 см2/сек, rc = 10 см, kh/μ =30 d см/спз, Q0 = 1000 см3/сек, рпл = 200 кгс/см2. Точные значения искомых параметров: a*1 = 191,74, a*2 = 2,65·10–3, а характерные значения ошибок μ1 = 2,19, μ1 = 2,5·10–4.
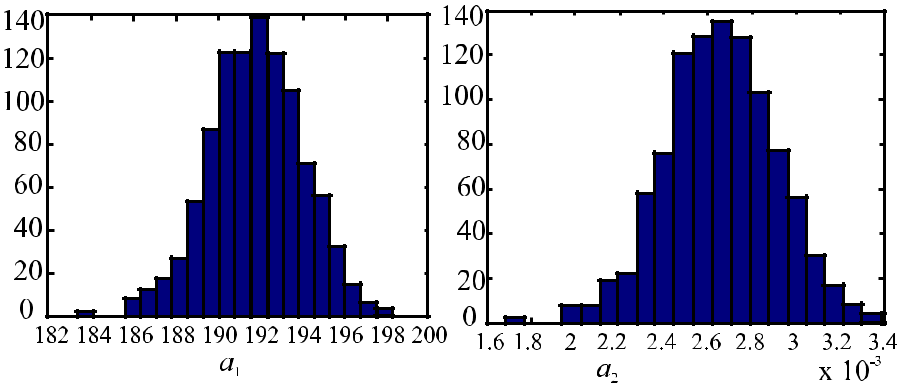
Рис. 1 а, б
С практической точки зрения оценка погрешности расчета параметров пласта зависит от выхода Q0 скважины, погрешности измерения давления σ i, местоположения измеренных времен {ti }in=1, количества n измерений, и так далее. Давайте сначала проведем такой качественный анализ. Для него допустим, что точность размеров σi = σ такая же. Давайте не будем заранее согласовывать параметры, которые нам нужны (тогда C0 – будет нулевой матрицей). Тогда согласно уравнению двумерная матрица C будет иметь следующие элементы:
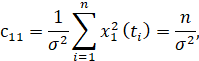
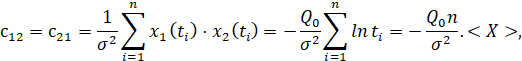
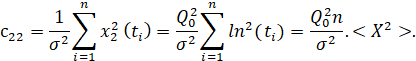
Где выражения для вектора параметром X = (ln(t1),..., ln(tn))' и A = (a1 ,..., an)' n – <A>, <A2>:
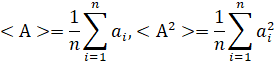
они представляют собой средние значения формы. Таким образом, согласно сделанным примечаниям, матрица C может быть записана следующим образом:
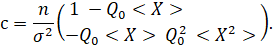
Поэтому в нем противоположная матрица получит вид:
Тогда:
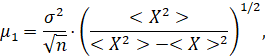
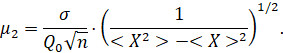 (4)
(4)
Теперь давайте рассмотрим более сложную схему анализа пласта. Допустим, что пласт не был воздействован в нулевой момент времени и скважина начинает работать с постоянным выходом Q(t) = Q0 и предположим, что после времени t = T скважина работает с новым постоянным выходом Q(t) = Q1. В этом случае давление в скважине сначала снижается, а затем после временного момента t = T начинает возрастать. При 0 < Q1 < Q0 схематическое изображение данного режима давления изображено на рис. 2а. Кривую изменения давления (КИД) можно разделить на две части: кривую снижения давления (КСД) часть I на рисунке 1a, и кривую восстановления давления (КВД) в части II. Таким образом, если Q1 ≠ 0 кривая восстановления давления (КВД) восстанавливается не полностью (рисунок 2 a).
Кривая снижения давления (КСД) I часть разрабатывается по описанной выше схеме. Для разработки кривой восстановления давления (КBД) часть II, давление можно записать в следующем виде:
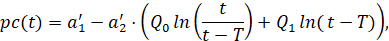
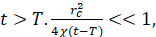 (5)
(5)
где:
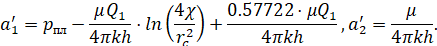 (6)
(6)
Если:
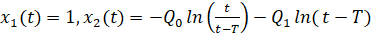 (7)
(7)
Если ввести обозначение t = T, то уравнение (4) примет следующий вид
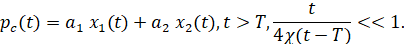 (8)
(8)
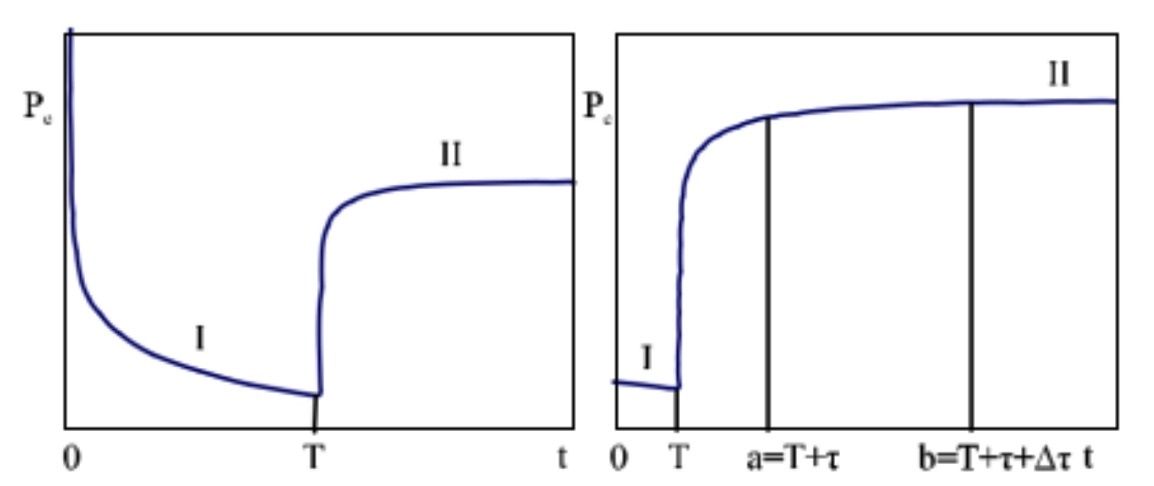
Рис. 2 а, б
Как и ранее, при измерении давления на практике допускаются погрешности. Следовательно, погрешности возникают, когда значения параметров a1′, a2′ вычисляются и эти погрешности вычисляются точно так же, как в уравнении (3), но вектор определяется уравнением 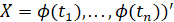 , где:
, где:
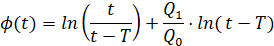 (9)
(9)
Информационная концепция и анализ определения неточностей параметров пласта
Таким образом, для частного случая в Примере 2 мы выразили погрешность определения неизвестного параметра при разработке КСД или КСД в форме единственного (3) уравнения. Пороги погрешностей, задаваемые (3) уравнением, прямо пропорциональны погрешностям измерения σ, а квадратный корень, полученный из чисел n измерений, обратно пропорционален. Затем, анализируя КСД, можно увидеть, что погрешности измерения для первого параметра не зависят от выхода Q0, а для второго параметра погрешности измерения обратно пропорциональны выходу скважины. Зависимость от доли времени подразделяется на отдельный множитель. Для анализа этой составляющей введем понятие информационной сети (информационность) τ=(t1,...,tn):
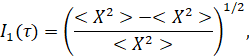
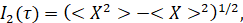 (10)
(10)
где: 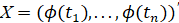 и
и
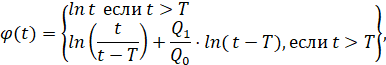 (11)
(11)
Погрешности в нем будут обратно пропорциональны информации сети размерностей 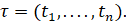 Если рассмотрим две части кривой изменения давления (КИД), измеренные во временных сетях
Если рассмотрим две части кривой изменения давления (КИД), измеренные во временных сетях 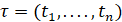 и
и 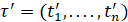 , то информация в оценке неизвестного параметра большая, сетевая погрешность мала. Существует фундаментальное (фундаментальное) различие между зависимостью измерительной сети для кривой снижения давления (КСД) и зависимостью информации измерительной сети от частей кривой восстановления давления (КВД). В первом случае информация сети определяется значением временной сети, но для части КВД информация сети также зависит от величин T и q = Q1/Q0 (см. уравнение 10).
, то информация в оценке неизвестного параметра большая, сетевая погрешность мала. Существует фундаментальное (фундаментальное) различие между зависимостью измерительной сети для кривой снижения давления (КСД) и зависимостью информации измерительной сети от частей кривой восстановления давления (КВД). В первом случае информация сети определяется значением временной сети, но для части КВД информация сети также зависит от величин T и q = Q1/Q0 (см. уравнение 10).
Для частей КСД И КВД a ≤ t ≤ b в свободном сечении I1(a, b), I2(a ,b) при информативности ti = a + (i – 1) · ∆t, i = 1,...,n при информативности равно размерных сетей при → ∞ Ik (a,b) = limn→∞ Ik (t1,...,tn) его можно определить как предел, где: ∆ t = (b – a)/(n – 1) – шаг сети. Если учесть эти выражения, то получаем:
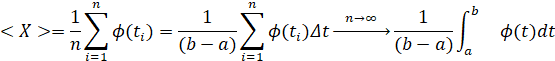
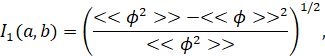
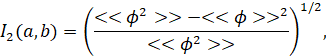 (12)
(12)
тогда:
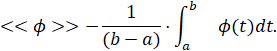
Рассмотрим рисунок 2. Из уравнения (11) очевидно, что в части I КСД расстояние (τ, τ + ∆τ) уменьшается наравне с увеличением информативности (∆τ отмечено). Это вытекает из следующих простых результатов: 1) Функция φ(t) в части I ровно увеличивается φ(t) = lnt << φ 2>> средне, и на расстоянии (τ, τ + ∆τ) с увеличением τ постепенно увеличивается; 2) С увеличением τ отклонение значений функции φ(t) во внутренних точках интервала (τ, τ + ∆τ) равномерно уменьшается.
Трудно точно сказать, как поведут себя информаторы в части II (КВД) I1(a,b), I2(a,b). Действительно, для КBД в сечении a = T + τ ≤ t ≤ T + τ + ∆τ = b рассмотрим информаторы I1(a,b), I2(a,b) (рисунок № 2 b.). На рисунках 3a-3b и 4a-4b изображены графики зависимости информаторов I1(a,b), I2(a,b) от величины τ , T = 4 часа (рисунок 3 а и б) и T=8 часов (рисунок 4a, б), показаны на графиках в часах. Во всех случаях значение параметра q принималось равным q=0,5. Таким образом, к разным кривым были применены разные значения параметра Δτ (1,2,3,4 и 5 часов соответственно).
На рисунках 2a-2б показаны два значения параметра q: q=0 (рисунок 2a) и q = 0,9 (рисунок 2 б), которые показывают связи информативности I2(a,b) (связь (I1(a,b) аналогично).
Как видно из этих изображений, зависимость информации от местоположения расстояний, их длины и величин T и q, которые являются внешними параметрами, очень сложно.
Как видно из рисунков 3 и 4, длительность T КСД влияет на самое низкое информационное значение и самое низкое значение кривой.
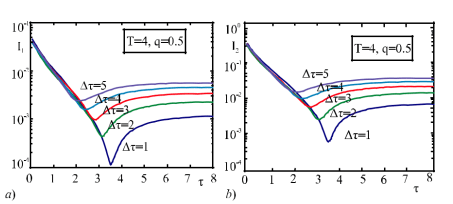
Рис. 3 а, б
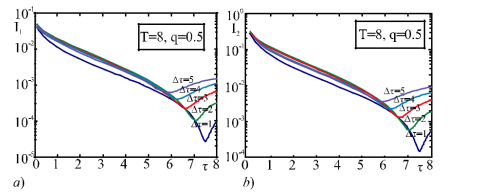
Рис. 4 а, б
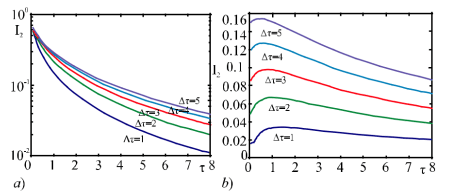
Рис. 5 а, б
Кроме того, влияние продолжительности измеренного расстояния на информацию об этом расстоянии очень интересно с практической точки зрения. Рисунки 3 и 5 показывают, что на этот вопрос нельзя однозначно ответить. Если τ ≤ τ0 (τ0 = 2 часа), то информация об интервале ∆τ = 2 часа (T+ τ, T + τ + ∆τ) для значений T = 4 и q = 0,5 практически не зависит от его продолжительности. Если τ>τ0, то начинает отчетливо ощущаться зависимость информации от величины τ. Параметры T и q существенно влияют на величину τ0. Как видно из рисунка 4, прирост значения T в 2 раза приводит к увеличению величины q в 2,5 раза. Однако, как видно из рисунка 5, в других случаях параметра q информация может зависеть от продолжительности интервалов измерения всех частей КВД.
Более общая модель неточностей
На практике измеренное значение давления на забое скважины pc(t) отличается от его фактической величины:
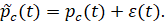
где: ε(t) – погрешность измерения (погрешность измерительного прибора). Мы рассматриваем ε(t) как стационарную случайную функцию, среднее значение которой равно нулю (< ε(t) > ≡ 0), распределенную по закону Гаусса. Он определяется своей корреляционной функцией Bε(τ):
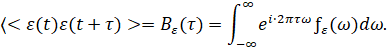
где: fε(ω) – ε(t) спектр случайной функции. Он выражается преобразованием Фурье корреляционной функции:
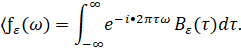
Неточность измерения является простейшей моделью ε(t) и служит «белым шумом». Значения неточностей для «белого шума» в разные моменты времени не коррелированы: < ε(t1) ε(t2) > = 0 если: t1 ≠ t2, < ε2(t) > = σ2.
В более сложных моделях измерений учитывается корреляция между значениями погрешностей в разных единицах времени. В этом случае для моделирования погрешности удобно использовать спектральную функцию fε(ω). В расчетах используем стационарные случайные функции, рандомизированную модель [3, 4]. Эта модель определяется следующим уравнением:
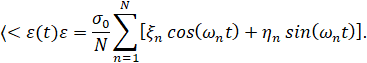
где: N – количество гармоник, (обычно N ≈ 100), 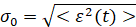 – среднеквадратичная неточность (среднеквадратичная погрешность). Спектральная функция выражается следующим уравнением:
– среднеквадратичная неточность (среднеквадратичная погрешность). Спектральная функция выражается следующим уравнением:
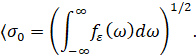
ξn, η n, n = 1,..., N – случайные (некоррелированные) Гауссовские стандартные случайные величины (то есть средние значения равны нулю, расщепление равно одному), ωn n = 1,..., N – не имеющее отношения друг к другу и одновременно также не связанные со случайными величинами ξn, ηn, n = 1,..., N с
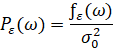 – равнозначные деления вероятной величины.
– равнозначные деления вероятной величины.
Будет использовано два типа Pε(ω) – “цветной шум”
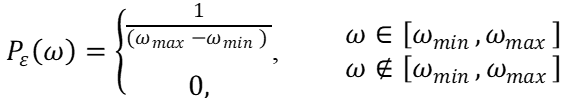
где: ωmin = 1/Tmax, ωmax = 1/Tmin, Tmin, Tmax – соответственно минимальное и максимальное значения времени, присущие корреляции;
– экспоненциальная корреляционная функция: Bε (τ) = σ02 exp(−, | τ | / T0 ) соответственно:
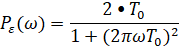
Уравнения моделирования для двух рассмотренных случаев соответственно следующие:
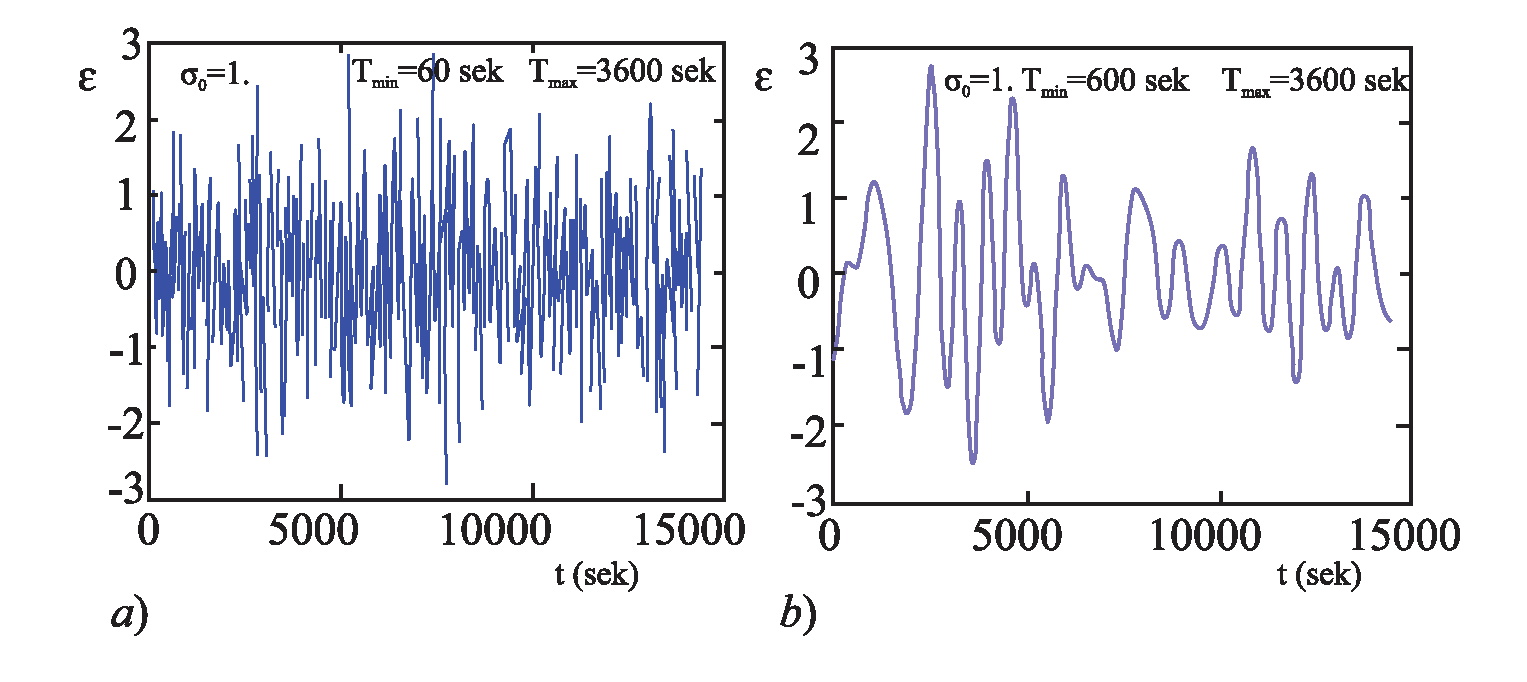
Рис. 6 а, б
где: γ – случайная величина псевдослучайного распределения на расстоянии [0,1]. На рисунках 6a – 6б показаны графики процесса ε (t) в случае «цветового шума»: Tmin = 60 сек., Tmax = 3600 сек. (рисунок 6 а) и Tmin = 600 сек, Tmax = 3600 сек. (рисунок 6 б). Аналогичным образом изображения для экспоненциальной корреляционной функции приведены на рисунках 7a – 7б.
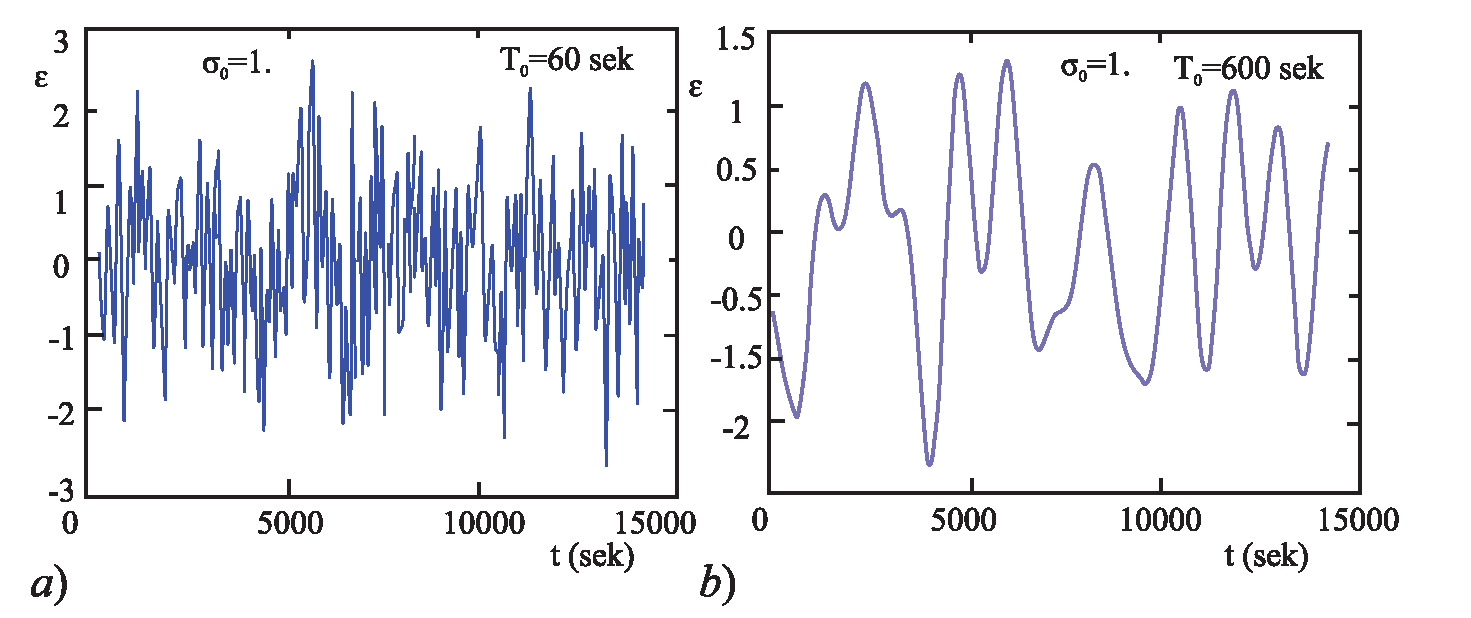
Рис. 7 а, б
Неточности измерения давления добавляют погрешности к коэффициентам A1, B1, A2, B2 вычисленным с помощью КИД (кривая изменения давления). Эти неточности неразрывно связаны с входными параметрами проблемы (гидро- и пьезопроводимость, выходы в начальное и конечное время, параметры, характеризующие неточности измерения давления и т. п.). Теперь рассмотрим данный вопрос.
На рисунке 8 а показана точная кривая давления (тонкая кривая) и ее кривизна (жирная кривая) с учетом неточностей. Корреляционная функция погрешности считалась экспоненциальной. Значения параметров: χ=1000 см2/с, rc = 10 см, K = kh/μ = 30 d см/спз, Q0 = 5000 см3/с, Q1 = 2500 см3/с, рпл =200 кгс/см2, σ0 = 2 кгс/см2, T0 = 600с. На рисунке 8 б изображен график ε(t), полученный путем моделирования кривых на рисунке 8 а.Относительные неточности определения коэффициентов A1, B1, A2, B2 путем анализа КИД равны 0,7, 0,75, 1,7 и 4,4% соответственно.
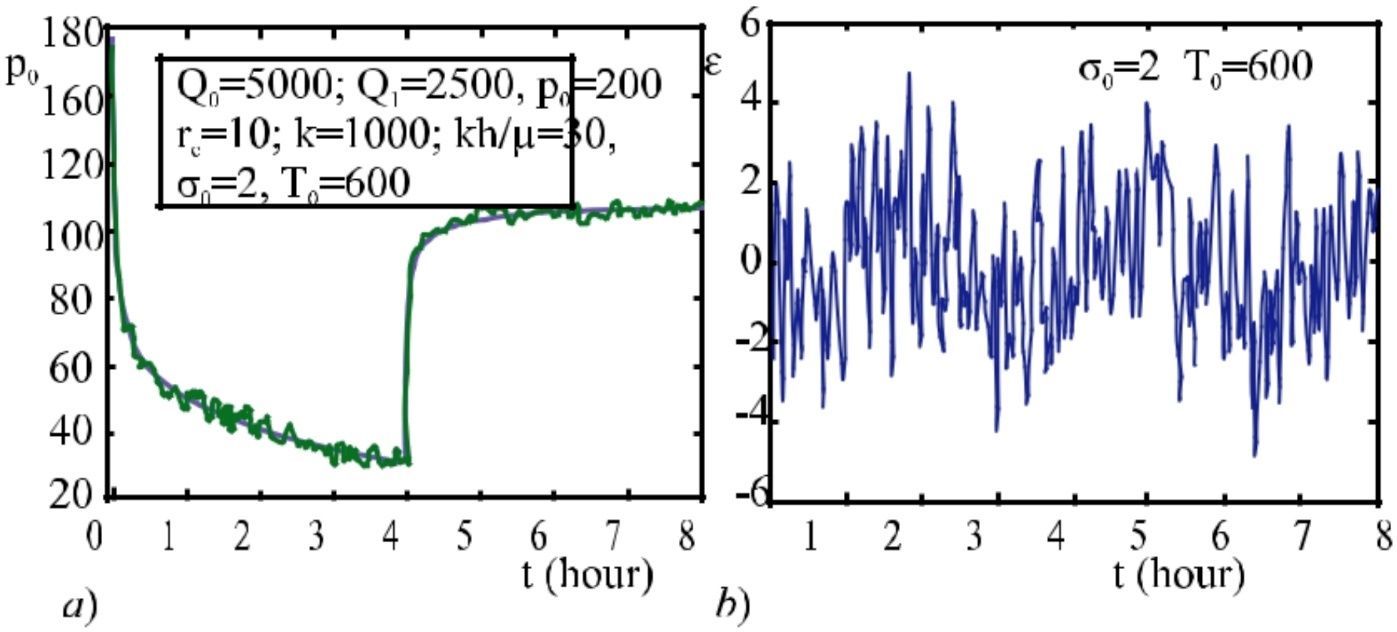
Рис. 8 а, б
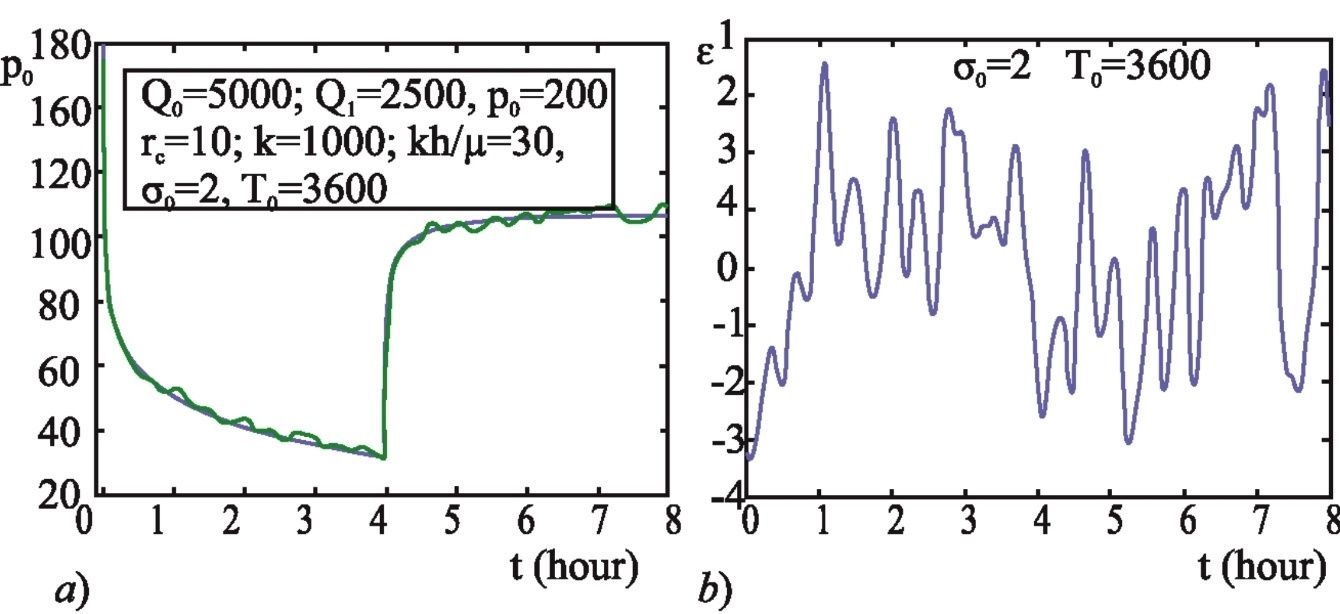
Рис. 9 а, б
При тех же условиях, но когда T0 = 3600 с КИД на рисунке 9 a, график неточностей ε(t) построен на рисунке 9б. Следует отметить, что с течением времени до T0 относительная погрешность коэффициентов A1, B1, A2, B2 увеличивается. Точнее, они составляют 4,46, 6,62, 5,8 и 13,9% соответственно.
Таким образом, структура функции корреляции погрешности измерения давления явно влияет на неточность, возникающую при нахождении коэффициентов A1, B1, A2, B2. С ростом присущего времени T0 также увеличивается точность нахождения коэффициентов.

.png&w=640&q=75)