В настоящее время известны результаты многих исследований, направленных на улучшение свойств дорожных покрытий: характеристики традиционного битума оптимизируются путем введения различных модификаторов [1-5]. При этом модифицированные битумы стали использоваться и в других отраслях, поскольку полимерные модификаторы, например, этиленвинилацетат (ЭВА) или отходы полиэтиленового производства, позволяют в несколько раз увеличить срок службы битумных строительных материалов, тем самым значительно экономя ресурсы: энергетические, материальные и трудовые.
Модифицированный битум, который отвечал бы современным требованиям улучшения эксплуатационных свойств покрытия, позволяет создать сочетания следующих условий: изучение свойств как самих нефтяных битумов, так и полимерно-битумных вяжущих, выбор оптимального метода планирования эксперимента и обработки данных, а также разработка простой и в то же время точной математической модели.
Чаще всего целью исследования сложных многокомпонентных систем становится нахождение наиболее приемлемого состава и построение зависимости свойств от данного состава и режима обработки. Такой системой, например, и является смесь нефтяного битума и модификатора.
Рассмотрим, какие методы планирования эксперимента и обработки данных применяются для выбора точной математической модели в технологии подбора оптимальной концентрации модификаторов для битумного вяжущего.
Необходимо учитывать, что при проведении эксперимента осуществляются некоторые упрощения/допущения. При этом корректность математической модели, а также возможность ее применения на практике зависят от правильного планирования эксперимента, учёта значимых факторов при построении зависимости и верной объективной интерпретации полученных результатов. Следовательно, сбор и обработка данных при проведении эксперимента должны проводиться с применением строгих методов математической статистики.
Особенность методов теории планирования экспериментов заключается в том, что они направлены на оптимальное планирование экспериментов при заданной точности и достоверности получения результатов, что позволяет сократить объем проводимых опытов и извлечь из полученных данных максимум полезных сведений. Преимуществом является и то, что экспериментальные данные, полученные указанными методами, могут стать основой для использования и других математических, статистических методов.
Существует несколько методов планирования эксперимента. Самым простым из них является полный факторный эксперимент (ПФЭ). Его суть заключается в том, что проводят определённое количество опытов, где все факторы принимают значения в заданном интервале, и экспериментально находят соответствующее значение функции у, называемой параметром цели. Но при использовании данного метода количество проводимых опытов слишком велико, из-за чего исследователи отдают предпочтение дробно факторному эксперименту (ДФЭ) типа 2k–p. При использовании этого метода из k факторов отбирают k–p основных, после чего строят план ПФЭ. Этот метод является более удобным, так как он сохраняет свойства ПФЭ при меньшем числе проводимых опытов. Дробность реплики выбирают с учётом того, что число коэффициентов модели не должно превышать число опытов и должно быть таким, чтобы реплика была симметричной, ортогональной, выполняла условия нормировки.
Метод эволюционного планирования основан на факторном эксперименте. Его осуществляют около некоторой начальной точки, которая определяется из условий эксперимента. Интервал варьирования выбирают его так, чтобы факторы не выходили за область допустимых значений. После этого проводятся опыты в точках факторного (ПФЭ или ДФЭ) плана.
Метод Гаусса-Зейделя и другие аналогичные итерационные методы часто применяются на практике благодаря их простоте. Сущность метода Гаусса-Зейделя заключается в последовательном движении к экстремуму путем поочередного варьирования каждым фактором до достижения частного экстремума функции отклика. При проведении эксперимента исследователи поочередно меняют значение одного фактора и стабилизируют в данной серии опытов другие факторы. К недостаткам метода можно отнести то, что сходимость итерационных процессов может быть медленной, что приводит к большой трате времени. Если число независимых переменных больше пяти, то применение метода Гаусса-Зейделя становится неэффективно.
При оптимизации градиентным методом движение совершается в направлении наибольшего изменения критерия оптимизации, т. е. в направлении градиента целевой функции. Направление движения корректируется после каждого рабочего шага, таким образом, каждый раз заново определяется значение градиента по результатам специально поставленных пробных экспериментов.
Метод крутого восхождения (метод Бокса-Уилсона) объединяет характерные элементы методов Гаусса-Зейделя и градиента. Крутое восхождение – это движение в направлении градиента функции отклика. Градиент задается частными производными, а частные производные функции отклика оцениваются коэффициентами регрессии. В крутом восхождении независимые переменные изменяют пропорционально величинам коэффициентов регрессии и с учетом их знаков. Составляющие градиента однозначно получаются умножением коэффициентов регрессии на интервалы варьирования по каждому фактору. Серия опытов в направлении градиента рассчитывается последовательным прибавлением к основному уровню факторов величин, пропорциональных составляющим градиента.
Реализацию начинают с опыта, условия которого выходят за область эксперимента хотя бы по одному из факторов. Для неадекватной модели один-два опыта выполняют в области эксперимента. Возможно проведение сразу всех мысленных опытов. При движении по градиенту возникают различные ситуации, определяющие принятие дальнейших решений.
Для планирования эксперимента в однофазных многокомпонентных смесях чаще всего используют симплексные решётки Шеффе [6]. Этот способ часто используют и для оптимизации временных затрат на подбор состава модифицированного битумного вяжущего с необходимыми механическими и реологическими свойствами.
Симплекс – это выпуклая геометрическая фигура, которая образована из n+1 точки в n-ном пространстве. Для k-компонентной системы обычно используют (k-1)-мерный симплекс. Суть метода симплексных решёток состоит в том, что в зависимости от выбранной модели составы размещаются в определенных точках: на вершинах симплекса, на середине ребер или в центре фигуры. Благодаря такому расположению точки распределяются равномерно по всему симплексу, а получаемая система уравнений позволяет быстро вычислить коэффициенты полинома. После выбора математической модели происходит переход к соответствующей симплексной решетке, а составление матрицы планирования сводится к определению состава экспериментальных точек.
На рисунке представлены примеры симплексных решёток для трёхкомпонентной системы.
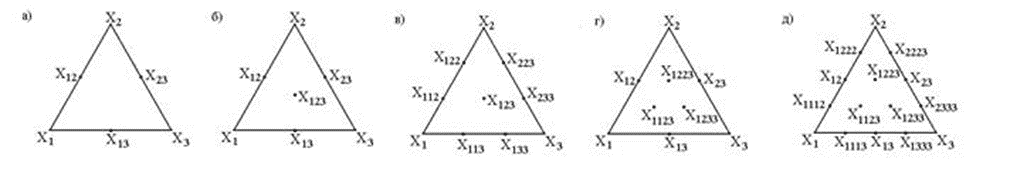
а – модель второй степени; б – модель неполной третьей степени; в – модель третьей степени; г – модель неполной четвертой степени; д – модель четвертой степени
Рис. Симплексные решетки для трехкомпонентной системы
Для построения диаграмм состав-свойство методом симплексных решёток используется следующий алгоритм:
- Выбор математической модели;
- Составление матрицы планирования;
- Вычисление коэффициентов уравнения регрессии;
- Проверка адекватности выбранной модели;
- В том случае, если модель адекватна – графическая интерпретация модели и расчет доверительных интервалов. Если модель неадекватна – выбор математической модели более высокой степени.
При составлении матрицы планирования считают, что количество коэффициентов полинома выбранной математической модели не должно превышать количество экспериментальных составов. При расположении составов на диаграмме необходимо учитывать, что коэффициенты для всей системы должны определяться с одинаковой точностью. Несмотря на большую вариативность размещения экспериментальных точек, чаще всего применяют симплекс-решетчатые, симплекс-центроидные и симплекс-симметричные планы Шеффе [7].
После выбора подходящего плана и составления матрицы планирования рассчитывают коэффициенты полиномиального уравнения проводят статистический анализ полученных данных.
Для того чтобы проверить адекватность выбранной модели, проводят опыты в контрольных точках. Чтобы правильно выбрать количество точек и разместить их на симплексе, нужно изучить область диаграммы, которая представляет наибольший интерес. Также на выбор контрольных точек влияет задача, стоящая перед исследователем, сложность опытов, экономические затраты и т.д.
Среди рассмотренных методов планирования эксперимента и обработки данных для многокомпонентной битумной смеси с модификаторами одним из наиболее оптимальных является метод симплексных решёток, поскольку он позволяет значительно сократить объем эксперимента при изучении систем с большим количеством компонентов. При использовании данного метода отпадает необходимость в пространственном представлении сложных поверхностей, так как свойства можно определить из уравнений. Также сохраняется возможность графической интерпретации результатов.

.png&w=640&q=75)