Большинство процессов реального мира, например, природные, экономические, финансовые, изменяются во времени. Для математического представления такого рода данных используется понятие временного ряда, которое и означает данные о чем-либо, собранные с разницей во времени.
Такие наборы данных полезно анализировать, чтобы находить некоторые статистические закономерности и полезные характеристики ряда, что поможет в понимании природы данных и будущем моделировании.
Одна из главных целей анализа и изучения временных рядов – их прогнозирование. Это часто используется в экономике, бизнесе для предсказывания будущих тенденций. Один из популярных способов прогнозирования временных рядов – построение авторегрессионных моделей.
Учитывая то, как много процессов можно представить в виде временного ряда, можно сделать вывод об актуальности темы для любых сфер бизнеса. Авторегрессия применяется для анализа и прогнозирования временных рядов. Рассмотрим это понятие более подробно.
Временной ряд или ряд динамики – последовательность статистических данных, о состоянии исследуемого процесса, выраженные числовым или факторным значением, полученных в разные моменты или интервалы времени. Каждому значению, описывающему временной ряда должно быть сопоставлено время проведения измерения или порядковый номер измерения [1].
О возникновении временного ряда, как правило, говорят в результате многократных измерений показателей тех или иных характеристик системы. Это могут быть показатели природных, социально-экономических явлений и процессов или данные о состоянии технологической системы. Например, стоимость квадратного метра жилого помещения, при анализе которого стремятся выявить основное направление развития, т.е. тренд. Или анализ объёма спроса на продукцию компании с целью расчёта ожидаемых остатков на складе.
Динамический ряд отличается от обычной выборки данных, так как при анализе рассматривается зависимость параметров от времени, а не только взаимосвязь характеристик и их статистические особенности [2].
На рисунке 1 представлен пример графика временного ряда.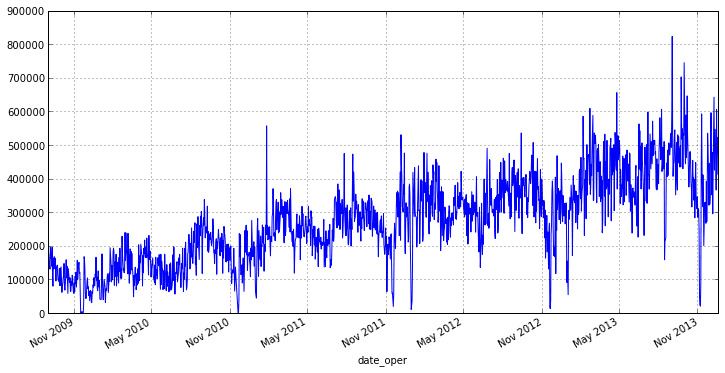 
Рис. 1. График временного ряда
В любом временном ряде можно выделить следующие составляющие: тренд, сезонную составляющую (сезонность), циклическую составляющую и случайную составляющую (ошибка):
- тренд – долгосрочное постепенное изменение ряда, это самая простая модель тренда, так как она демонстрирует долгосрочный рост или спад;
- сезонность – предсказуемые, краткосрочные модели, которые возникают в течение определенного периода времени и повторяются бесконечно;
- циклическая составляющая – долгосрочные колебания данных, которые могут длиться годы или десятилетия, такие колебания происходят непредсказуемо и часто являются результатом внешних экономических условий;
- ошибка – случайные колебания вследствие неконтролируемых обстоятельств.
Первые три компоненты составляют неслучайную составляющую временного ряда. Случайная составляющая обязательно содержится во временном ряде. При этом ряд может не иметь одной или нескольких, возможно всех, неслучайных компонент [4].
Анализ временных рядов – совокупность статистических методов для выявления отдельных компонентов временного ряда и создания прогноза его значений в различные моменты времени [3]. Анализ временных рядов включает в себя методы изучения временных рядов, имеющие цель как понять природу точек данных, так и пытающиеся построить прогноз.
Авторегрессионная модель основана на модели линейной регрессии. Рассмотрим регрессионную модель и понятия, связанные с ней.
Регрессия (лат. regressio – обратное движение) в статистике – это статистическая зависимость математического ожидания случайной величины от значений другой случайной величины или нескольких случайных величин [5].
Отличительной особенностью регрессионной зависимости от функциональной является её многозначность. Функциональная зависимость y=f(x), сопоставляет значение аргумента x с единственным значением y, в регрессионной модели каждому значению аргумента может соответствовать несколько значений параметра y.
Если при каждом значении x=xi наблюдается ni значений yi1,…, yini величины y, то зависимость средних арифметических
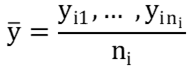(1)
от xi, i=1,…,N и является регрессией в статистическом понимании данного термина [6].
Многие задачи, целью которых является поиск отношения между двумя и более переменными. Регрессионный анализ хорошо подходит и часто используется для решения подобных задач. Одним из основных направлений применения является прогнозирование.
Цель регрессии – поиск зависимости между исходной переменной и несколькими регрессорами (факторами). При этом методом определения коэффициентов может выступать метод наименьших квадратов или метод максимального правдоподобия [7].
Для нахождения и описания тренда при анализе временного ряда удобно использовать регрессионные модели. Независимым аргументом, в таких моделях выступает время.
Основные виды регрессионной модели, применяемые в анализе временных рядов:
- простая линейная регрессия;
- множественная регрессия;
- нелинейная регрессия.
Рассмотрим эти виды регрессии.
Линейная регрессия является простейшим видом регрессионной модели. Основой модели выступает гипотеза, о существовании дискретного внешнего фактора X(t), имеющего влияющий на рассматриваемый процесс Z(t), связь между фактором и процессом представима в виде линейной функции. Модель прогнозирования временного ряда на основании линейной регрессии описывается уравнением:
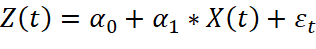, (2)
где α0 и α1 – коэффициенты регрессии; εt – ошибка модели.
На рисунке 2 представлен график, на котором данные выборки обозначены синими точками, а регрессионная зависимость – сплошной линией.
Для получения прогноза значений процесса Z(t) в момент времени t обязательным является иметь значение X(t) для того же момента времени t, что редко достижимо в реальных условиях. На практике на процесс Z(t) оказывают влияние множество дискретных внешних факторов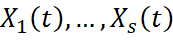 
. Тогда модель прогнозирования имеет вид:
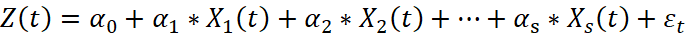, (3)
где α0,α1,…,αs – коэффициенты регрессии; εt – ошибка модели.
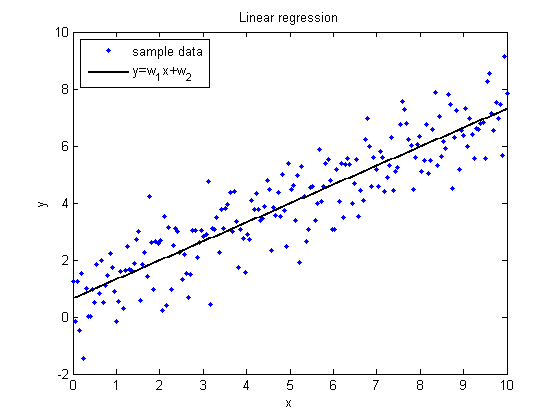
Рис. 2. Пример построения линейной регрессии
Недостатком данной модели является сложность в достижении на практике знания всех факторов X1(t),…, Xs(t), для определения Z(t).
Основой нелинейной модели является гипотеза о существовании известной функции:
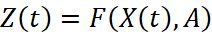(4)
где Z(t) – исходный процесс; X(t) – внешний фактор, от которого зависит процесс Z(t); A – функция, параметры которой необходимо определить в рамках построения модели прогнозирования.
На практике нелинейные регрессионные модели применяются не часто, так как малая часть процессов, вид функциональной зависимости которых заранее известен.
Поскольку при оценке зависимости одних случайных величин от других регрессионные модели не учитывают фактор времени, они слабо применимы для анализа временных рядов. Для прогнозирования временных рядов используют авторегрессию.
Авторегрессия
В статистике авторегрессионная (AR) модель является представлением случайного процесса. Такие модели используется для описания определенных изменяющихся во времени природных, экономических и других процессов.
Статистическая модель является авторегрессионной, если она предсказывает будущие значения на основе прошлых. Например, предсказание будущих цен акций на основе их прошлых значений.
В контексте временных рядов авторегрессионная модель – модель временных рядов, в которой значения временного ряда в данный момент линейно зависят от предыдущих значений этого же ряда.
На рисунке 3 представлен пример графика авторегрессионной модели на фоне значений временного ряда.
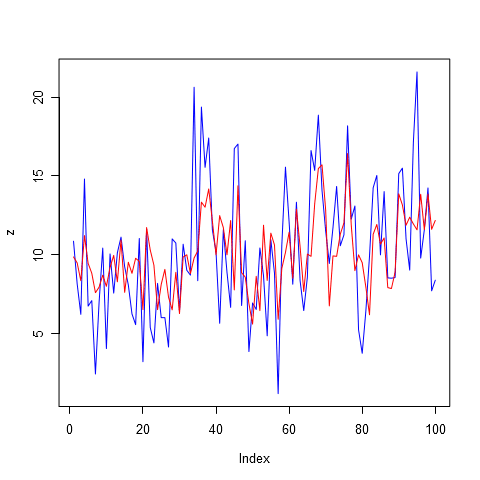
Рис. 3. Пример авторегрессии
Авторегрессионный процесс порядка p (AR(p)-процесс) определяется следующим образом [8]:
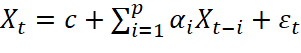(5)
где α1,…,αp – параметры модели (коэффициенты авторегрессии); c – постоянная; εt – случайная составляющая (влияние внешних факторов).
Простейшим примером будет являться авторегрессионный процесс p = 1 AR(1) – процесс, в котором текущее значение основано только на значении в предшествующий момент времени [9]:
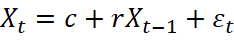(6)
Такой процесс именуется Марковским случайным процессом, согласно которому значения процесса Z(t) в любой момент времени t определяются по значениям в предыдущий момент t-1 (и случайной составляющей); такую модель также называют «случайным блужданием».
Авторегрессия по своей сути является регрессионной моделью, в которой в качестве независимых аргументов участвуют лаговые переменные. Если ввести лаговый оператор L:Lxt=xt-1, то авторегрессионную модель можно записать следующим образом:
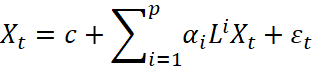(7)
или
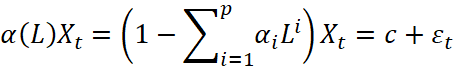(8)
Авторегрессия используется в анализе временных рядов, а именно при их прогнозировании. На основе уже имеющихся статистических данных возможно обучить авторегрессионную модель (найти ее коэффициенты), после чего с ее помощью можно попытаться спрогнозировать дальнейшие тенденции роста и падения значений временного ряда.
Таким образом, авторегрессионные модели используются для прогнозирования временных рядов. Модель использует предыдущие значения ряда для получения следующего. Для вычисления коэффициентов модели используются различные методы, но самый надежный и простой – метод наименьших квадратов.
Главным преимуществом является то, что все алгоритмы из класса авторегрессионных моделей имеют четкое математико-статистическое обоснование, это делает авторегрессионные модели одними из наиболее научно обоснованных из всего разнообразия используемых методов прогнозирования временных рядов.
Но авторегрессионные модели имеют и недостатки. Одним из них является требование к временным рядам: для подбора точной модели требуется довольно большая выборка, что на практике не всегда возможно. Также большим недостатком является низкая адаптивность модели: при получении новых данных того же ряда модель нужно периодически дообучать.
Тем не менее, модели авторегрессии остаются актуальными, так как показывают хорошие результаты при грамотном применении.
