О силе отталкивания в гравитационном законе Ньютона

В современных учебниках по физике (см. например, [5], с. 303-307) формулу для силы тяготения F определяют так

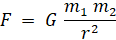    (1)

где G=(6,6732±0,0031)•10^-11Hм²кг^-2 есть так называемая гравитационная постоянная, m₁ и m₂ – массы тяготеющих тел, а r – расстояние между этими телами. Силу F называют силой всемирного тяготения. При этом авторство формулы (1) приписывается Ньютону. Также считается, что численное определение гравитационной постоянной G выполнено английским физиком Кавендишем (1731 – 1810) в 1798 году.

Однако подробный анализ знаменитого сочинения Ньютона [4] свидетельствует о том, что формула (1) в этом сочинении отсутствует. Из приведённых рассуждений в [4] по поводу тяготения можно привести только следующую словесную формулировку закона тяготения.

Тяготение существует на всех планетах (с. 514 в [4]).

Тяготение, направляющееся к любой из планет, обратно пропорционально квадратам расстояний мест до центра её (с. 514 в [4]).

Тяготение существует ко всем телам и пропорционально массе каждого из них (с. 518 в [4]).

Следует обратить внимание на то, что в указанных формулировках Ньютон выражает физические закономерности не в виде равенств, а в форме пропорциональностей. Эта форма пропорциональности присутствует во всех закономерностях, полученных Ньютоном в [4].

Отсутствие в рассуждениях Ньютона аналитической формулы для закона тяготения позволило последующим исследователям при решении задач небесной механики создавать различные количественные соотношения для закона тяготения, в которых величины коэффициента пропорциональности различны.

Рассмотрим следующие две теоремы Ньютона, которые использовались в [1] при выводе аналитической формы закона тяготения.

Теорема 1. Два взаимно притягивающихся тела описывают и около своего общего центра тяжести и друг около друга подобные траектории (с. 217 в [4]).

Действительно, расстояние тел от их общего центра тяжести обратно пропорционально их массам, следовательно, отношение этих расстояний постоянно, тогда постоянно и отношение каждого из них к полному расстоянию между телами. Кроме того, эти расстояния обращаются около своего общего конца с одинаковым угловым движением, вследствие чего, не наклоняясь друг к другу, располагаются по одной прямой. Прямые же линии, отношение длин которых постоянно и которые поворачиваются около своих концов на равные углы, описывают вокруг этих концов на плоскостях, находящихся вместе в покое или движущихся без вращения, подобные фигуры. Следовательно фигуры, описываемые сказанными расстояниями, подобны между собой.

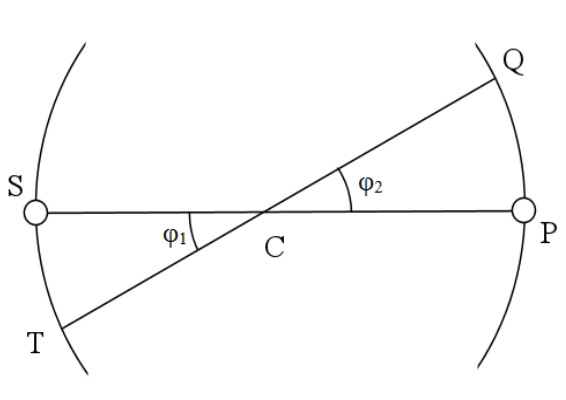
Рис. 1. Система двух взаимодействующих тел

Это доказательство рассматриваемой теоремы можно пояснить, используя рисунок 1. На нем показана система двух взаимодействующих тел S и P. При угловом движении двух тел S и P вокруг центра тяжести С углы φ₁ и φ₂ равна, а дуги ST и PQ подобны. Следовательно, траектории этих тел при движении вокруг центра тяжести подобны и центростремительная сила обоих тел будет направлена к точке С.

Если в этой системе движение тела Р рассматривать относительно тела S, то траектория такого движения будет подобна траектории тела Р относительно точки С. Аналогичное можно сказать и о траектории тела S относительно тела Р.

Таким образом, все возможные траектории в этой системе (рис.1) подобны и они могут быть представлены любой из плоских кривых второго порядка, а центростремительная сила как сила притяжения будет направлена по линии SP.

Далее Ньютон доказывает следующую теорем.

Теорема 2. Если два тела притягиваются взаимно с какой бы то ни было силою и поэтому обращаются около своего общего центра тяжести, тоя утверждаю, что под действием такой же силы каждое тело может описывать вокруг другого неподвижную фигуру, равную и подобную тем, которые они описывают друг около друга (с. 217-219 в [4]).

Доказательство Ньютон строит следующим образом.

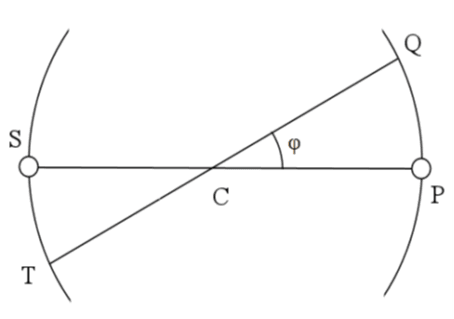
Рис. 2. Движение двух тел вокруг их центра тяжести

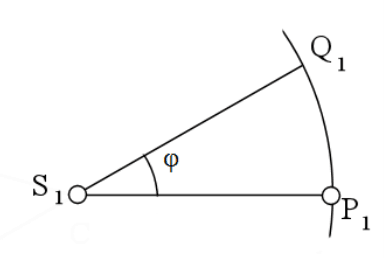
Рис. 3. Относительное движение одного тела вокруг другого

Пусть два тела S и Р (рис. 2) обращаются около своего общего центра тяжести С на угол , перемещаясь от S к Т и от Р к Q.

Теперь в данном движении тел выделим движение тела Р относительно S. В таком случае тело S как бы остановлено и его положение фиксируется неподвижной точкой S₁ (рис. 3). Из точки S₁ проведем прямую S₁Р₁ = SР и прямую S₁Q₁ параллельную прямой ТQ. Так как S₁Р₁ = S₁Q₁, то дуга Р₁Q₁ (рис. 3) суть траектория движения тела Р в его перемещении относительно тела S.

Дуги Р₁Q₁, РQ, SТ подобны, так как они опираются на один тот же угол φ. Если учесть, что точка S₁ подвижна и перемещается по дуге SТ (рис. 2), то дуга Р₁Q₁ не только подобна дуге РQ, но и равна ей.

Аналогичные рассуждения можно провести, рассмотрев движение тела S относительно тела Р.

Из предыдущих теорем следует, что если относительное движение тела Р происходит по эллиптической кривой, в фокусе которой находится тело S, то тело Р притягивается к телу S под действием центростремительной силы, направленной от Р к S и обратно пропорциональной квадрату расстояния между Р и S. Обозначим эту центростремительную силу через F₁, а расстояние между рассматриваемыми телами через r.

Рассматривая относительное движение тела S по эллиптической орбите, в фокусе которой находиться тело Р, мы будем иметь силу F₂, направленную от S к Р и также обратно пропорционально квадрату расстояния между телами S и Р.

Эти две силы F₁ и F₂, приложенные к телам Р и S, определяют силу взаимодействия между ними, которую Ньютон назвал силой притяжения.

Согласно третьему закону Ньютона, модули противоположно направленных сил F₁ и F₂ равны. Это может иметь место только в том случае, если

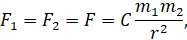    (2)

где m₁ и m₂ – массы тел S и Р, а F есть сила притяжения между двумя телами, движущимися по эллиптическим траекториям.

Направление силы F определяется выбором относительного движения одного из тел. Например, по второму закону Кеплера все планеты движутся по эллиптическим орбитам, в одном из фокусов которого находится Солнце. Следовательно, в данном случае рассматривается движение планет относительно неподвижного Солнца и центростремительная сила, приложенная к планете, направлена к Солнцу.

В формуле (2) множитель C суть коэффициент пропорциональности, который может содержать как размерную, так и безразмерную составляющую. Обычно размерные коэффициенты пропорциональности зависят от единиц измерения и позволяют правые и левые части физических формул свести к одинаковой размерности. Безразмерные же коэффициенты пропорциональности как отвлечённые числа определяют во сколько раз левая часть формулы больше или меньше правой и могут быть как положительными, так и отрицательными величинами.

Исходя из сказанного, в самом общем случае множитель C в (2) определим так

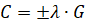,    (3)

где G – гравитационная постоянная, которая представляет размерный коэффициент пропорциональности, а λ – безразмерный коэффициент пропорциональности. Знак минус в (3) отражает то, что силы F₁ и F₂ направлены в противоположные стороны.

Теперь после подстановки (3) в (2) получаем следующую формулу для закона тяготения

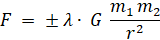    (4)

Формула (4) описывает две силы: одна из них – сила притяжения, а другая – отталкивания. Очевидно, что эти силы имеют разные знаки. Один из вариантов приписывания названным силам определённых знаков может быть таким.

Рассмотрим взаимодействие двух тел в условиях выполнения третьего закона Ньютона – действие равно противодействию. Пусть действие первого тела на второе осуществляется силой F₁, приложенной к первому телу. Второе тело действует на первое силой F₂, приложенной ко второму телу. Если теперь эти равные и противоположно направленные силы перенести в центр первого тела, то сила F₁ будет притягивать первое тело ко второму, а сила F₂ будет отталкивать первое тело от второго. В этом случае силу F₁ назовём силой притяжения, припишем ей знак плюс и в рамках формулы (4) определим эту силу так

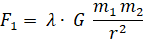    (5)

Силу F₂ в данном рассмотрении назовём силой отталкивания, припишем ей знак минус и определим её так

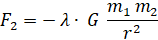    (6)

Из формул (5) и (6) следует, что F₁+F₂=0, что означает выполнимость для этих сил третьего закона Ньютона.

Некоторые авторы силе притяжения приписывают знак минус, но это делается для того, чтобы потенциал этой силы был величиной положительной.

Для согласования знаков в формулах (5) и (6) с кинематическими характеристиками движения рассмотрим движение тела по эллиптической траектории, в левом фокусе которой находится Солнце. В этом случае большая ось эллипса пересекает траекторию в двух точках. Одна из них афелий является наиболее удалённой от фокуса. Расстояние афелия до левого фокуса вдоль большой оси эллипса обозначим через r₁. Вторая точка перигелий есть ближайшая к левому фокусу. Расстояние до фокуса этой второй точки обозначим через r₂. Скорости тела в указанных точках обозначим через v₁ и v₂. Можно показать, что скорости v₁ и v₂ обратно пропорциональны расстояниям r₁ и r₂, то есть справедливо соотношение v₁∙ r₁  v₂ ∙ r₂ = const, что в свою очередь означает: v₁ = v_min есть минимальная скорость, а v₂=v _max – максимальная скорость, при этом r₁ > r₂.

Пусть тело начинает движение со скоростью v₁ от точки афелия, удалённой от фокуса на расстоянии r₁ до точки перигелия. Радиус вектор которой суть r₂. Уже отмечалось, что скорость тела в перигелии равна v₂. Так как v₁ < v₂, то тело на указанном участке траектории движется ускоренно. Работу силы тяготения F₁ определим так

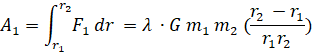    (7)

Так как r₁ > r₂, то на этом участке траектории работа A₁ представляется отрицательной величиной.

Заметим, что на этом участке траектории тело приближается к левому фокусу, в котором расположено Солнце, следовательно сила F₁, определяемая по формуле (5) суть сила притяжения.

Далее ввиду замкнутости траектории тело начинает удаляться от точки перигелия до точки афелия в результате чего скорость уменьшается от v₂ до v₁, то есть тело движется замедленно. Очевидно, то на этом участке траектории работа A₂ силы F₂ оказывается равной

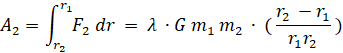∙    (8)

Из формул (7) и (8) следует, что A₁  A₂, но величины этих работ – отрицательны.

Таким образом, сила притяжения F₁, определяемая по формуле (5), вызывает ускорительное движение на участке эллиптической траектории от точки афелия до точки перигелия. При возвратном движении от перигелия до афелия тело движется замедленно под действием силы отталкивания F₂, определяемой по (6).

Для изучения структуры формулы (4) выделим в ней в качестве множителя величину

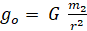,    (9)

размерность которой соответствует размерности ускорения. Если в ней в качестве m₂ принять массу Земли, равную 5,9726 ∙ 10²⁴ кг, r  6,378 ∙ 10⁶ м считать радиусом Земли, а величину G полагать равной 6,6732 ∙ 10^-11 Нм²кг^-2 , то расчётом по (9) получаем 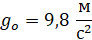. Полученная таким путём величина g_o совпадает с величиной ускорения свободного падения на Землю любого тела.

Теперь силу притяжения (5) с учётом (9) переписываем так

,

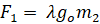которая при λ=1 переходит в силу тяжести тела массой m₂. В формуле (4) введём дополнительное обозначение: α=±λ, после чего с учётом (9) ей придадим следующую форму

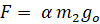.     (10)

Формула (10) представляет уточнённую форму второго закона Ньютона, в которой введён коэффициент пропорциональности  . Такое уточнение впервые выполнено в [2] и там же показано, что α > 0 для ускоренных движений, а для замедленных движений α < 0.

С помощью формулы (10) в [3] произведён аналитический анализ расчётов известного опыта Толмина и Стюарта, который доказывает электронную природу тока в металлах.