Законы движения были впервые сформулированы Ньютоном в его «Principia Philosophial Naturalis» [3].
Прежде чем сформулировать второй закон движения словами Ньютона, необходимо указать на две величины, которые ввел Ньютон. Первую из них он назвал количеством материи и дает ей следующее определение: количество материи есть мера таковой, устанавливаемая пропорционально плотности и объему её. Отсюда совершенно ясно, что количество материи есть масса. Вторую величину Ньютон называет количеством движения и определяет её так: количество движения есть мера такового, устанавливаемая пропорционально скорости и массе. Если скорость обозначим через а массу через , то эта величина пропорциональна или просто равна 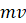 .
.
Следует заметить, что результаты своих исследований Ньютон представлял не в форме равенств, а в форме пропорциональностей. Эта форма пропорциональностей присутствует во всех задачах, рассмотренных в [3]. В частности формулировка второго закона движения согласно [3] (см. стр. 40) гласит: изменение количества движения пропорционально приложенной действующей силе и имеет то направление, в котором эта сила действует. Под изменением количества движения следует понимать разность 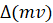 , отнесённую к единице времени.
, отнесённую к единице времени.
Из сказанного и следует формула второго закона движения:
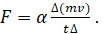 (1)
(1)
Здесь введён эмпирический коэффициент пропорциональности α. В физических задачах, представляемых в формульном виде, коэффициенты пропорциональности могут быть как размерными величинами, и безразмерными в виде отвлечённых чисел. Размерные коэффициенты пропорциональности правые и левые части какой-либо физической формулы приводить к одинаковой размерности. Если же в формуле левые и правые части имеют одинаковые размерности, то безразмерный коэффициент пропорциональности указывает на то во сколько раз левая часть указанной формулы больше или меньше правой.
В данном случае применительно к формуле (1) коэффициент пропорциональности α суть безразмерная величина, которая в рамках той или иной задачи, может быть как положительной, так и отрицательной величиной [1, 2].
Если в (1) положить α р авном единице, то данная формула примет вид
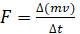 , (2)
, (2)
который гласит: действующая сила F равна изменению количества движения, что противоречит утверждению Ньютона, изложенному выше. Однако формула (2) используется во всей научной и учебной литературе по физике в качестве количественной формулы второго закона Ньютона.
В действительности же формула (2) устанавливает размерность силы F через размерность величин, входящих в правую часть (2), и определяет единицу измерения силы F в той или иной системе единиц, принятых в качестве основных. В таком случае коэффициент α в (1) определяет во сколько раз действующая сила F больше или меньше единичной.
Чтобы формуле (1) придать современный вид необходимо в правой части (1) осуществить предельный переход, устремив промежуток времени ∆t к нулю. После чего получим
F 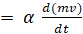 , (3)
, (3)
где соотношение 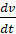 означает ускорение.
означает ускорение.
В работе [1] формула (3) использовалась при анализе движения электрона в электромагнитном поле в результате чего произведено обобщение известной формулы Альберта Эйнштейна, определяющей зависимость массы электрона от скорости.
В условиях постоянства массы m формула (3) принимает более простой вид
F 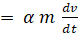 . (4)
. (4)
В работе [2] формула (4) при отрицательном значении величины α использовалась при аналитическом анализе результатов известного опыта Толмина и Стюарта, который доказывает электронную природу тока в металлах.
Для выяснения физического смысла коэффициента пропорциональности α соотношение (4) перепишем так:
F dt = α mdv. (5)
В рамках общеизвестных представлений ведём элементарный импульс силы dK =F∙dt и элементарный импульс тела dL = mdv, после чего из (5) получаем формулу для определения α в следующем виде
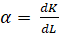 . (6)
. (6)
Левая часть в формуле (5) определяет количественную форму действия силы F на тело в течение времени dt, результатом которого является величина элементарного количества движения, характеризующего скорость движения. В связи с чем формула (6) является мерой превращения силы в движение.
При выводе формулы (4) предполагалось, что движение тела происходит вдоль прямой линии. Однако в декартовой системе координат x, y, z движение тела по криволинейной траектории раскладывается на три движения. Именно, движение вдоль оси x, определяемое функцией x(t), вдоль оси y, определяемое как y(t) и вдоль оси z, определяемое функцией z(t). Скорости тела при указанных движениях обозначим через u вдоль оси x, v вдоль оси y, w вдоль оси z. Составляющие вектора силы на оси x, y, z обозначим через X, Y, Z соответственно. Теперь в каждом из этих движений указанные силы будем определять по формуле (4) при условии, что коэффициент пропорциональности α принимает значения α1, α2, α3. После чего будем иметь
X = α1 m 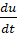 , Y = α2 m
, Y = α2 m 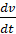 , Z = α3 m
, Z = α3 m 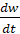 . (7)
. (7)
Для получения дифференциальных уравнений, определяющих функции x(t), y(t) и z(t) необходимо кинематические соотношения u = 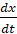 , v=
, v= 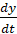 , w
, w 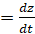 подставить в правые части уравнений (7). После указанной подстановки получаем следующие обыкновенные дифференциальные уравнения второго порядка
подставить в правые части уравнений (7). После указанной подстановки получаем следующие обыкновенные дифференциальные уравнения второго порядка
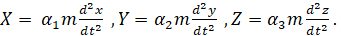 (8)
(8)
Эти уравнения представляют математическую модель механики Ньютона. В рамках этой модели определяются две задачи механики материальной точки. В первой задаче по заданным кинематическим соотношениям правых частей в (8) определяются силы X, Y, Z. Во второй задаче по заданным силам X, Y, Z вычисляются кинематические параметры движения x(t), y(t) и z(t).
В качестве примера использования уравнений (8) рассмотрим задачу о движении тела, брошенного под углом θ к горизонту, с начальной скоростью v0 в условиях, когда на него действует только сила тяжести. Будем предполагать, что α1 = α2 = α3 = α и что движение происходит в плоскости yx, где y – вертикальная ось а x – горизонтальная. В данном случае действующие силы таковы:
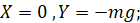
где m есть масса брошенного тела а g – ускорение свободного падения. Знак минус во втором соотношении означает, что направление силы тяжести противоположно положительному направлению оси y. Для нашего случая дифференциальные уравнения (8), определяющие координаты тела x(t) и y(t) выглядят так:
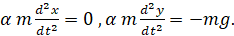 (9)
(9)
Интегрируем первое уравнение в (9) и получаем 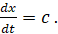
Произвольная постоянная c этого уравнения определяется по начальным условиям: тело брошено со скоростью v0 и в начале движения имело скорость по оси Ox:
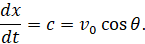
Интегрируем найденное управление снова и находим:
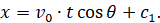
Для точки O имеем x=0 , t=0, следовательно, c1=0 и последнее соотношение примет окончательный вид:
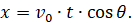 (10)
(10)
Для интегрирования второго уравнения в (9) представим его в виде:
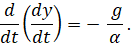
После его интегрирования находим
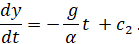
Для определения c2 заметим, что при t=0 будет 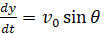 (проекция v0 на ось Oy). Тогда
(проекция v0 на ось Oy). Тогда 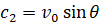 и теперь последнее уравнение напишется так:
и теперь последнее уравнение напишется так:
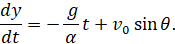
Интегрируем это уравнение получаем
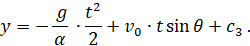
Для определения c3 замечаем, что в начале координат, при y=0, имеем t=0, тогда из последнего соотношения находим, что с3=0, и уравнение для определения координаты y принимает окончательный вид:
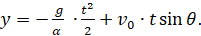 (11)
(11)
Подставляя в это уравнение значение t из уравнения (13), находим
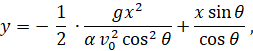
что окончательно дает
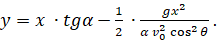 (12)
(12)
Уравнение (12) описывает траекторию движения тела и позволяет исследовать характерные кинематические параметры этой траектории.
Действительно, дальность полёта тела вдоль оси x будет определяться тем значением x=xm, при котором y =0. Следовательно, для определения дальности полёта тела правую часть в (12) приравниваем нулю и получаем следующее соотношение для определения xm
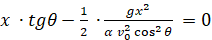 ,
,
из которого определяем
xm 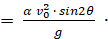 (13)
(13)
Для определения максимальной высоты подъёма тела необходимо функцию y=y(x), определяемую по формуле (12), исследовать на экстремум. В этом случае вычисляем производную 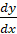 и приравниваем её нулю. В результате этих действий получаем соотношение
и приравниваем её нулю. В результате этих действий получаем соотношение
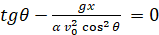 ,
,
из которого определяется xo как точка экстремума равная
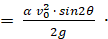 (14)
(14)
Для нахождения максимальной высоты ym необходимо полученное значение xo подставить в (12) после чего будем иметь
ym 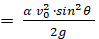 (15)
(15)
Из (13) и (14) следует, что xo = 12 xm. Следовательно, кривая траектории симметрично относительно точки xo.
Докажем, что кривая, определяемая формулой (12), суть парабола. Для этого в (12) перейдём к новым координатам x' и y' согласно следующим формулам x = x' + a, y = y' + b. После этого в новой системе координат уравнение (12) принимает вид
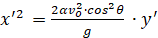 , (16)
, (16)
если выполняются следующе условия
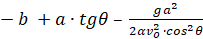 =0
=0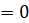 ,
,
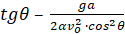 =0
=0 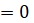 (17)
(17)
Соотношения (17) служат для определения параметров a и b данного преобразования. Действительно, из (17) получаем
a 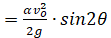 , b
, b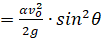 . (18)
. (18)
Из анализа формул (14), (15) и (18) рассматриваемые преобразования координат можно переписать так :
x = x' + xo, y = ym- y'. (19)
Вернёмся к соотношению (16) и ведём в нём параметр,
P = 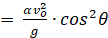 , (20)
, (20)
После чего указанное соотношение принимает вид
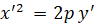 . (21)
. (21)
Из аналитической геометрии известно, что уравнение (21) представляет каноническое уравнение параболы, а множитель P суть параметр данной параболы.
Итак, уравнение (12) описывает параболу. Следовательно, тело, брошенное под углом к горизонту, движется по параболической траектории, а при изменении угла θ от нуля до  получаются различные параболы.
получаются различные параболы.
Чтобы найти все поле, в точках которого может появляться тело, имеющее начальную скорость v0, необходимо найти огибающую всех параболических траекторий. Но прежде покажем общий способ получения уравнения огибающей по данному уравнению огибаемой.
Если мы имеем уравнение кривой вида:
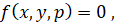 (22)
(22)
где x и y суть текущие координаты, а p – параметр, то вид этой кривой и положение ее на плоскости, характеризуясь параметром p, меняется с изменением p. Огибающую можно рассматривать как геометрическое место пределов пересечения кривых, происходящих от изменения параметров в уравнении кривой. Если в данном уравнении кривой параметр p изменится в 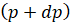 , то уравнение кривой будет таково:
, то уравнение кривой будет таково:
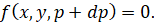
Разлагая это уравнение в ряд Тейлора с учетом первых двух членов, получаем:
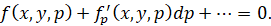
Это соотношение с учетом (22) упрощается так:
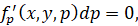
но ввиду того, что dp≠0, получаем окончательно:
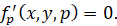 (23)
(23)
Исключая параметр p из уравнений (22) и (23), получаем уравнение огибающей в форме:
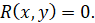
Применим эти рассуждения к нахождению огибающей параболических траекторий тела, брошенного под углом к горизонту.
Рассмотрим уравнение (12) как уравнение одной из парабол и за параметр p примем величину tgθ, т. е. положим tgθ=p. Тогда входящая сюда величина 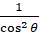 выразится так:
выразится так:
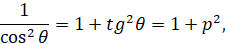
и уравнение (12) напишется в виде:
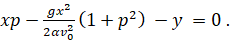 (24)
(24)
Дифференцируя (24) по p, согласно (23), находим
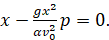 (25)
(25)
Исключаем теперь параметр p из (24) и (25), тогда и получим искомое уравнение огибающей. Действительно, из (25) имеем
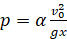 .
.
Подставим это значение p в уравнение (24), после чего получим уравнение огибающей:
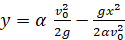 . (26)
. (26)
Это уравнение представляет тоже параболу. Точки пересечения ее с осями координат определяется так:
с осью x: 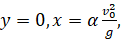
с осью y: 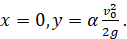
Таковы значения координат точек пересечения огибающей параболы с осями x и y.
Отнесем полученное уравнение (26) к новой системе координат ξNɳ, начало которой поместим в точке N. Тогда имеем формулы перехода:
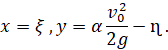
В новой системе координат уравнение (26) примет вид:
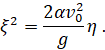
Следовательно, огибающая парабола имеет вершину в N, ось ее есть Nη, а параметр параболы равен α 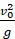 .
.
Данная огибающая парабола делит плоскость всевозможных траекторий движения материальной точки на две области: область безопасную, лежащую выше огибающей, и область, лежащую ниже огибающей, в которой могут находиться всевозможные траектории. Очевидно, что различные значения параметра α, входящего в уравнение (26), построят семейство огибающих, которые при α>1 будут увеличивать площадь безопасной области, а при α<1 - уменьшать. Этот факт следует учитывать при постановке задач механики на данную тему.

.png&w=640&q=75)