К вопросу об устойчивости вычисления корней полинома в зависимости от возмущения коэффициентов

Введение и постановка вопроса. Нахождение корней полиномов – одна из основных задач алгебры, к которой сводятся приложения во множестве областей научных исследований [1-3]. В частности корни характеристического полинома матрицы линейной системы обыкновенных дифференциальных уравнений определяют характер устойчивости системы [4]. Однако реально идентифицировать корни полиномов сложно по причине трудоемкости вычислений и накопления погрешности, поэтому классические методы часто строятся не на прямых, а на косвенных методах определения свойств корней. К числу основных препятствий относят вычислительную неустойчивость, под которой понимается резкий рост погрешности значений корней в зависимости от погрешности определения (возмущения) полиномиальных коэффициентов [5]. Вычислительные трудности увеличиваются, если корни полинома отделены на малую величину [2]. Компьютерная реализация обостряет проблемы вследствие того, что данные обрабатываются с плавающей точкой на разрядной сетке фиксированной длины, что само по себе влечет плохо контролируемое накопление погрешности. Алгоритмы вычисления корней полинома принято считать неустойчивыми независимо от способа нахождения корней [5]. В [5] приводится пример, когда коэффициент полинома

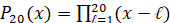,     (1)

при x¹⁹ возмущается на 2^-23, –

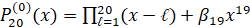,     (2)

β₁₉=2^-23, – в результате больше половины корней полинома (2) становятся комплексными, один из остальных отличается от соответственного корня (1) уже в первых знаках после десятичной точки. Это полностью подтверждается идентификацией корней (2) по представленной ниже программе, где подпрограмма func примет вид

function func (var x: extended): extended;

var i1: 1..n1; p: extended;

begin p:=1; for i1:=1 to 20 do p:=p*(x-i1); func:=abs(p+sqr(sqr(sqr(sqr(x))))*x*x*x*exp(-23*ln(2))); end;

В [6, 7] и более детально в [8, 9], а также в [10] предложен метод идентификации корней полинома на основе алгоритма сортировки, при этом большинство вычислительных операций заменяются на операции сравнения. Вычислительные операции требуются только для задания сравниваемых значений полиномов. В результате погрешность нахождения корней существенно снижается: как правило, сохраняются все значащие цифры мантиссы каждого корня в формате представления данных.

Излагаемая работа отвечает на вопрос о пределах возмущения коэффициентов полинома, в границах которых метод вычисления корней на основе сортировки сохраняет значащие цифры этих корней в формате представления данных. В этой работе исследование ограничивается случаем вещественных корней, вопросы устойчивости комплексных корней затронуты в [10].

Об идентификации корней полиномов на основе сортировки слиянием по матрицам сравнений. Корни полинома идентифицируются как минимумы модуля этого полинома. Согласно принципу минимума модуля [11] модуль аналитической функции, отличной от константы и не обращающейся в ноль внутри области аналитичности, не может иметь локальных минимумов внутри этой области. Отсюда локальные минимумы модуля полинома достигаются в тех и только тех точках, где он обращается в ноль. Все эти локальные минимумы могут быть конструктивно идентифицированы при помощи устойчивой адресной сортировки. Метод детально изложен в [8] для случая вещественных корней полинома, в [9] – для случая комплексных корней, при этом для простоты описания использована устойчивая сортировка подсчетом по матрицам сравнений. Сортировка слиянием по матрицам сравнений для этой цели применяется в [10]. В излагаемом ниже сообщении используется только сортировка слиянием по матрицам сравнений (кратко сортировка). Все особенности ее применения детально описаны в [10], для краткости здесь это описание опускается. Вместе с тем реализующая предлагаемый подход программа приводится, практически она без изменения заимствуется из [10]:

program ITERREKORN1680ANNA;

{$APPTYPE CONSOLE} uses SysUtils;

const n1=40; b: array [1..n1] of extended = (1, 1.0001, 2, 2.0001, 3, 3.0001, 4, 4.0001, 5, 5.0001, 6, 6.0001, 7,

7.0001, 8, 8.0001, 9, 9.0001, 10, 10.0001, 11, 11.0001, 12, 12.0001, 13, 13.0001, 14, 14.0001, 15, 15.0001, 16,

16.0001, 17, 17.0001, 18, 18.0001, 19, 19.0001, 20, 20.0001);

eps=1E-44; n00=1512; mm=4; type vect1=array [0..4*n00] of extended; vect2=array [0..4*n00] of longint;

vec=array [0..n1] of extended; var i,j,k,l,ee,nn0,kk,kk1: longint; a,c: vect1; e: vect2; rex:vect1;

aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1,x00,x11,eps0,h,eps00: extended;

procedure sort(var nn0:longint; var c: vect1; var e: vect2);

type vecc=array[0..4*n00] of longint; var ab:integer; i,j,k,l,m,r,nm,p,n: longint; e1,e2: vecc;

begin p := trunc(ln(nn0)/ln(2)); if p<> ln(nn0)/ln(2) then p := p+1; n := round(exp(p*ln(2)));

for l := 1 to n do if l<=nn0 then e[l] := l else ab:=1; for r := 1 to p do begin m :=round(exp(r*ln(2)));

nm:=n div m; for k := 0 to nm-1 do begin for l := 1 to m div 2 do begin

if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab := l else e1[l] := e[k * m + l];

if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab := 1

else e2[l] := e[k * m + m div 2 + l] end; i := 1; j := 0; while i + j <= m do begin

if i = m div 2 + 1 then ab := -1; if j = m div 2 then ab := 1;

if (k * m + i > nn0) or (e[k * m + i]>nn0) or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)

then ab:=1; if (i <= m div 2) and (j <= m div 2 -1) and (k * m + i<= nn0) and (k * m + m div 2 + j <= nn0-1)

then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab := 1 else

begin if c[e2[j + 1]] - c[e1[i]]= 0 then ab := 0; if c[e2[j + 1]] - c[e1[i]]> 0 then ab := 1;

if c[e2[j + 1]] - c[e1[i]]< 0 then ab := -1 end; if ab >= 0 then begin e[k * m + i + j] := e1[i]; i := i + 1 end

else begin e[k * m + i + j] := e2[j + 1]; j := j + 1 end end end end end;

procedure ident (var x00,x11,eps0, h: extended);

label 21, 22;

{polinom stepeni 1680}

function func (var x: extended): extended;

var i0,i1,i2: integer; p,p0,p1: extended;

begin p:=1; for i0:=1 to n1 do p:=p*(sqr(x)-sqr(b[i0]));

p1:=1; for i1:=1 to n1 do for i2:=1 to 1{0} do p1:=p1*(sqr(x)-sqr(b[i1]+i2*0.001));

p0:=1; for i1:=1 to n1 do for i2:=1 to 1{0} do p0:=p0*(sqr(x)-sqr(b[i1]-i2*0.001));

{func:=abs(p*p1*p0);} {func:=abs(p*p1*p0+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+

1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+

1e-22*((sqr(sqr(sqr(x))))*x*x*x -1e-20*(sqr(sqr(sqr(x))))*x*x-1e-18*(sqr(sqr(sqr(x))))*x-

1e-16*(sqr(sqr(sqr(x))))-1e-12*((sqr(sqr(x))))*x*x*x-1e-8*((sqr(sqr(x))))*x*x-1e-4*((sqr(sqr(x))))*x-

1*sqr(sqr(x))-1.4*sqr(x)*x-1.8*sqr(x)-2.2*x-2.6);}

func:=abs(p*p1*p0+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+

1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+

1e-22*((sqr(sqr(sqr(x))))*x*x*x +1e-20*(sqr(sqr(sqr(x))))*x*x+1e-18*(sqr(sqr(sqr(x))))*x+

1e-16*(sqr(sqr(sqr(x))))+1e-12*((sqr(sqr(x))))*x*x*x-1e+8*((sqr(sqr(x))))*x*x-1e+4*((sqr(sqr(x))))*x+

1*sqr(sqr(x))+1.4*sqr(x)*x+1.8*sqr(x)+2.2*x+2.6);

end;

procedure min1 (var x: extended;var ee:longint);

begin min:=func(x); ee:=0; for i:=1 to mm do begin

x:=xk0+i*h0; if min > func(x) then begin min:=func(x); ee:=i; end;end;end;

begin

aaa:=1e62; nn0:=n00; hh:=nn0*h; kk:=0; x0:=x00; while x0 <= x11 do begin

for i:=1 to nn0 do begin x:=x0+i*h; c[i]:=func(x); end;

sort(nn0, c, e); k:=1; while k<= nn0 do begin for l := 1 to k-1 do

if abs(e[k]-e[k-l]) <= eps0/h then goto 22; xk:= x0+e[k]*h; eps1:=eps0;xk0:=xk-eps1;

xk1:=xk+eps1;h0:=abs(2*eps1)/mm; while abs(eps1) > eps do begin x:=xk0; min1(x,ee); eps1:=eps1/1.2;

xk0:=xk0+ee*h0-eps1; xk1:=xk0+ee*h0+eps1; h0:=abs(2*eps1)/mm; end; if func(xk)= 0 then begin x:=xk;

goto 21; end; x:=xk0+ee*h0+eps1;

for i:= 1 to 2 do begin z:=x+i*h; if func(x) >= func(z) then goto 22; end;

for i:= 1 to 2 do begin z1:=x-i*h; if func(x) >= func(z1) then goto 22; end;

if abs(aaa-x)<=1e-20 then goto 22;

21: writeln (' ', x,' ', func(x)); aaa:=x; kk:=kk+1; rex[kk]:=x;

22: k:=k+1 end; x0:=x0 + hh end; end;

begin writeln ('PRIBLIJENIE'); writeln; x00:=-32; x11:=32; eps0:=0.00049/2; h:=eps0/43; eps00:=eps0;

ident(x00,x11,eps0, h); writeln; writeln ('TOCHN'); writeln; eps0:=eps0/10; h:=eps0/43; for kk1:=1 to kk do

begin x00:=rex[kk1]-eps00; x11:=rex[kk1]+eps00; ident(x00,x11,eps0, h); end; readln; end.

Способ задания полинома детально оговаривается ниже. Программа построена на первоначальной локализации корней с относительно большим радиусом локализации, по ходу которой каждый локализованный корень запоминается. В окрестности каждого запомненного корня, ограниченной исходным радиусом локализации, выполняется повторный запуск всей процедуры с радиусом локализации столь малым, что он гарантирует идентификацию всех (возможно пропущенных при первоначальной локализации) корней полинома. Начальный радиус локализации меньше половины наименьшего расстояния между корнями, шаг дискретизации около 0.02 радиуса, эти величины могут быть уменьшены или увеличены в зависимости от характера задачи.

В разделе описаний процедуры ident из элементов массива b формируется входной полином с помощью подпрограммы func. По основной теореме высшей алгебры полином

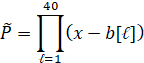    (3)
имел бы в качестве корней все 40 элементов массива b. Для увеличения степени полинома, корни которого требуется найти, полином (3) преобразовывался в полином степени 80:

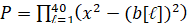.    (4)

У полинома (4) те же корни, что и у полинома (3), но кроме того в число корней входят все корни (3) с обратным знаком. Дальнейшее увеличение степени обеспечивает алгоритм:

p1:=1; for i1:=1 to n1 do for i2:=1 to 1{0} do p1:=p1*(sqr(x)-sqr(b[i1]+i2*0.001));

p0:=1; for i1:=1 to n1 do for i2:=1 to 1{0} do p0:=p0*(sqr(x)-sqr(b[i1]-i2*0.001));    (5)

Закомментирована возможность задания полинома степени 1680. В первом цикле алгоритм (5) к каждому корню полинома (4) десять раз добавляет по 0.001, образуя новые корни, и перемножает все разности квадратов независимой переменной и значения нового корня. Получается полином степени 80. Во втором цикле от каждого корня полинома (4) вычитается по 0.001, и полученные биномы аналогично перемножаются. Получается еще один полином степени 80. Затем значению func присваивается произведение всех трех полиномов: func:=abs(p*p1*p0); В результате на вход программы поступает полином степени 240, многие корни которого взаимно отделены на 0.0001. Результат работы программы (в колонке слева – значения корней, справа – соответственные значения полинома):

  -2.00001000000000E+0001   0.00000000000000E+0000

  -2.00000000000000E+0001   0.00000000000000E+0000

  -2.00000000000000E+0001   0.00000000000000E+0000

  -2.00001000000000E+0001   0.00000000000000E+0000

  -1.99990000000000E+0001   0.00000000000000E+0000

  -1.99991000000000E+0001   0.00000000000000E+0000

  -1.90010000000000E+0001   0.00000000000000E+0000

  -1.90011000000000E+0001   0.00000000000000E+0000

  …………………………………………………………….

  -2.99910000000000E+0000   0.00000000000000E+0000

  -2.99900000000000E+0000   0.00000000000000E+0000

  -3.00100000000000E+0000   0.00000000000000E+0000

  -3.00110000000000E+0000   0.00000000000000E+0000

  -2.00000000000000E+0000   0.00000000000000E+0000

  -2.00010000000000E+0000   0.00000000000000E+0000

  -1.99910000000000E+0000   0.00000000000000E+0000

  -1.99900000000000E+0000   0.00000000000000E+0000

  -2.00110000000000E+0000   0.00000000000000E+0000

  -2.00100000000000E+0000   0.00000000000000E+0000

   ……………………………………………………………

   1.90000000000000E+0001   0.00000000000000E+0000

   1.90001000000000E+0001   0.00000000000000E+0000

   1.99990000000000E+0001   0.00000000000000E+0000

   1.99991000000000E+0001   0.00000000000000E+0000

   2.00000000000000E+0001   0.00000000000000E+0000

   2.00001000000000E+0001   0.00000000000000E+0000

   2.00010000000000E+0001   0.00000000000000E+0000

   2.00011000000000E+0001   0.00000000000000E+0000

Согласно проверке найдены все 240 корней, которые вычислены без потери значащих цифр мантиссы в формате представления данных. Данный эксперимент уточняет результаты из [10]. Ненакопление погрешности достигается потому, что сортировка не преобразует входные значения, а только сравнивает их. Аналогично, при реализации схемы (2) используются только сравнения индексов, и в остальном программа построена на сравнении значений. Потеря точности возникает на входе, при вычислении значения полинома, что с ростом его степени может нарушать границы числового диапазона компьютера.

О влиянии возмущения коэффициентов полинома на идентификацию вещественных корней. Алгоритмы вычисления корней полинома принято считать неустойчивыми: независимо от способа нахождения корней на их значения крайне влияет возмущение коэффициентов полинома. В частности, для примера из [5], заданного соотношениями (1), (2) с приведенной во введении подпрограммой func программы ITERREKORN1680ANNA, где раздел инструкций берется с параметрами границ области корней и радиусов локализации

begin writeln (' ':12,'PRIBLIJENIE'); writeln; writeln;

x00:=-22; x11:=22; eps0:=0.00049; h:=eps0/43; eps00:=eps0; ident(x00,x11,eps0, h); writeln; writeln;

writeln (' ':12,'TOCHN'); writeln; writeln; eps0:=eps0/10; h:=eps0/43; for kk1:=1 to kk do

begin x00:=rex[kk1]-eps00; x11:=rex[kk1]+eps00; ident(x00,x11,eps0, h); end; readln; end.

получится следующий результат работы программы:

   1.00000000000000E+0000   1.19209289550781E-0007

   2.00000000000000E+0000   2.67926726706873E-0005

   3.00000000000019E+0000   5.58171556354209E-0005

   3.99999999973898E+0000   2.90234767774677E-0006

   5.00000007244851E+0000   1.26962299873412E-0006

   5.99999305644644E+0000   1.58001785166561E-0006

   7.00030339886563E+0000   9.00123268365860E-0007

   7.99302504437346E+0000   3.68803739547729E-0007

   9.14728137862023E+0000   2.23517417907715E-0007

   9.50201129715976E+0000   5.96046447753906E-0008

Однако при уменьшении возмущения рассматриваемого коэффициента до β¹⁹=2^-33 уже все 20 корней станут вещественными, а при β¹⁹=2^-43 все корни идентифицируются с точностью до 0.5×10^-4. Дальнейшее уменьшение возмущения влечет повышение точности приближения к значениям корней из (1), и при β¹⁹=2^-89 все корни окажутся найденными с верными значащими цифрами в принятом числовом формате [7]. Более того, даже если все коэффициенты полинома (1) (кроме старшего единичного) возмутить, причем на возрастающие значения по убыванию индекса коэффициента, вплоть до возмущений больших единицы в коэффициентах при степенях от четвертой до нулевой, 

function func (var x: extended): extended;

var i1: 1..n1;p:extended;

begin p:=1; for i1:=1 to 20 do p:=p*(x-i1); func:=abs(p+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+

1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+

1e-22*((sqr(sqr(sqr(x))))*x*x*x -1e-20*(sqr(sqr(sqr(x))))*x*x-1e-18*(sqr(sqr(sqr(x))))*x-

1e-16*(sqr(sqr(sqr(x))))-1e-12*((sqr(sqr(x))))*x*x*x-1e-8*((sqr(sqr(x))))*x*x-1e-4*((sqr(sqr(x))))*x-

1*sqr(sqr(x))-1.4*sqr(x)*x-1.8*sqr(x)-2.2*x-2.6); end;

все значения корней полинома совпадут с корнями невозмущенного полинома (1) при идентификации по представленной программе:

   1.00000000000000E+0000  -7.98899001000100E-0022

   2.00000000000000E+0000   2.82448607935987E-0019

   3.00000000000000E+0000   7.86974812262708E-0017

   4.00000000000000E+0000   7.39441869845990E-0015

   5.00000000000000E+0000   2.90985021530609E-0013

   6.00000000000000E+0000   6.17501469624645E-0012

   7.00000000000000E+0000   8.43767455081911E-0011

   8.00000000000000E+0000   8.31773124213909E-0010

   9.00000000000000E+0000   6.37567453464681E-0009

   1.00000000000000E+0001   4.00099999988385E-0008

   1.10000000000000E+0001   2.13281227462223E-0007

   1.20000000000000E+0001   4.03586937610926E-0007

   1.30000000000000E+0001   7.11606705941480E-0008

   1.40000000000000E+0001   8.33336454193886E-0008

   1.50000000000000E+0001   1.07542928787874E-0006

   1.60000000000000E+0001   7.41617575745599E-0006

   1.70000000000000E+0001   7.55488678400258E-0005

   1.80000000000000E+0001   2.07697876763876E-0004

   1.90000000000000E+0001   3.85618490701140E-0003

   2.00000000000000E+0001   9.83042047999998E-0003

Если такое же возмущение вставить в программу с полиномом, корни которого заданы в разделе констант исходной программы ITERREKORN1680ANNA, –

const n1=40; b: array [1..n1] of extended = (1, 1.0001, 2, 2.0001, 3, 3.0001, 4, 4.0001, 5, 5.0001, 6, 6.0001, 7,

7.0001, 8, 8.0001, 9, 9.0001, 10, 10.0001, 11, 11.0001, 12, 12.0001, 13, 13.0001, 14, 14.0001, 15, 15.0001,

16, 16.0001, 17, 17.0001, 18, 18.0001, 19, 19.0001, 20, 20.0001);

затем с помощью подпрограммы func задать полином степени 240 с корнями, взаимно отделенными на 0.0001 и на 0.001, при возмущении коэффициентов из предыдущего кода, 

function func (var x: extended): extended;

var i,i1,i2: integer;p,p1,p2:extended;

begin p:=1; for i:=1 to n1 do p:=p*(sqr(x)-sqr(b[i]));

p1:=1; for i1:=1 to n1 do for i2:=1 to 1 do p1:=p1*(sqr(x)-sqr(b[i1]+i2*0.001));

p2:=1; for i1:=1 to n1 do for i2:=1 to 1 do p2:=p2*(sqr(x)-sqr(b[i1]-i2*0.001));

func:=abs(p*p1*p2+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+

1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+1e-22*((sqr(sqr(sqr(x))))*x*x*x -

1e-20*(sqr(sqr(sqr(x))))*x*x-1e-18*(sqr(sqr(sqr(x))))*x-1e-16*(sqr(sqr(sqr(x))))-1e-12*((sqr(sqr(x))))*x*x*x-

1e-8*((sqr(sqr(x))))*x*x-1e-4*((sqr(sqr(x))))*x-1*sqr(sqr(x))-1.4*sqr(x)*x-1.8*sqr(x)-2.2*x-2.6); end;

и с разделом инструкций

begin writeln ('PRIBLIJENIE'); writeln; x00:=-22; x11:=22; eps0:=0.00049/10; h:=eps0/43; eps00:=eps0;

ident(x00,x11,eps0, h); writeln; writeln ('TOCHN'); writeln; eps0:=eps0/10; h:=eps0/43;

for kk1:=1 to kk do begin x00:=rex[kk1]-eps00; x11:=rex[kk1]+eps00;

ident(x00,x11,eps0, h); end; readln; end.

то программа найдет все 240 корней без потери значащих цифр их мантисс:

  -2.00001000000000E+0001   3.27710066015066E-0003

  -2.00000000000000E+0001   3.27677951999999E-0003

  -2.00000000000000E+0001   3.27677951999999E-0003

  -2.00001000000000E+0001   3.27710066015066E-0003

  -1.99990000000000E+0001   3.27356975449527E-0003

  -1.99991000000000E+0001   3.27389059723000E-0003

  -1.90010000000000E+0001   1.19797177811181E-0003

  -1.90011000000000E+0001   1.19809584508472E-0003

   ……………………………………………………………

  -2.00000000000000E+0000  -1.51293728063987E-0019

  -2.00010000000000E+0000  -1.51363433276626E-0019

  -1.99910000000000E+0000  -1.50667478257557E-0019

  -1.99900000000000E+0000  -1.50598016786007E-0019

  -2.00110000000000E+0000  -1.52061827515068E-0019

  -2.00100000000000E+0000  -1.51991878233121E-0019

  -1.00000000000000E+0000  -2.79081000999900E-0022

  -1.00010000000000E+0000  -2.79201607438174E-0022

   ……………………………………………………………

   1.90000000000000E+0001   3.85618490701140E-0003

   1.90001000000000E+0001   3.85655473826694E-0003

   1.99990000000000E+0001   9.82144592196409E-0003

   1.99991000000000E+0001   9.82234302818295E-0003

   2.00000000000000E+0001   9.83042047999998E-0003

   2.00001000000000E+0001   9.83131836319032E-0003

   2.00010000000000E+0001   9.83940281061152E-0003

   2.00011000000000E+0001   9.84030147140918E-0003

Данный эксперимент уточняет результат из [10] за счет меньшей взаимной отделенности корней. Само значение полинома в идентифицированных корнях остается возмущенным, – вычисленным с низкой точностью. В целом, это не ошибка, поскольку при возмущении коэффициентов идентифицируются корни другого (по сравнению с невозмущенным) полинома, и полученные значения корней совпали только в границах использованного формата числовых данных.

Наиболее парадоксально то, что у рассматриваемого полинома высокой степени коэффициенты при малых степенях, начиная, примерно, от x¹⁶, можно подвергать сильным возмущениям без потери правильности нахождения корней. Так, если положить

func:=abs(p*p1*p0+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+

1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+

1e-22*((sqr(sqr(sqr(x))))*x*x*x +1e-20*(sqr(sqr(sqr(x))))*x*x+1e-18*(sqr(sqr(sqr(x))))*x+

1e-16*(sqr(sqr(sqr(x))))+1e-12*((sqr(sqr(x))))*x*x*x-1e+8*((sqr(sqr(x))))*x*x-1e+4*((sqr(sqr(x))))*x+

1*sqr(sqr(x))+1.4*sqr(x)*x+1.8*sqr(x)+2.2*x+2.6); end;

где, в частности, возмущение при x⁶ составляет 10⁸, то это повлияет только на значение полинома в корнях, но не на сами корни:  

  -2.00001000000000E+0001   3.27646064415053E-0003

  -2.00000000000000E+0001   3.27613952320001E-0003

  -2.00000000000000E+0001   3.27613952320001E-0003

  -2.00001000000000E+0001   3.27646064415053E-0003

  -1.99990000000000E+0001   3.27292994967050E-0003

  -1.99991000000000E+0001   3.27325077320987E-0003

  -1.90010000000000E+0001   1.19750117319310E-0003

  -1.90011000000000E+0001   1.19762522530537E-0003

   ……………………………………………………………

  -2.00000000000000E+0000  -6.39968149254048E-0013

  -2.00010000000000E+0000  -6.40160165324149E-0013

  -1.99910000000000E+0000  -6.38242163400653E-0013

  -1.99900000000000E+0000  -6.38050626883012E-0013

  -2.00110000000000E+0000  -6.42082968051326E-0013

  -2.00100000000000E+0000  -6.41890471468716E-0013

   ……………………………………………………………

   1.90010000000000E+0001   3.85941412289775E-0003

   1.90011000000000E+0001   3.85978427561286E-0003

   1.90000000000000E+0001   3.85571444572533E-0003

   1.90001000000000E+0001   3.85608426212401E-0003

   1.99990000000000E+0001   9.82080611074092E-0003

   1.99991000000000E+0001   9.82170319776427E-0003

   2.00000000000000E+0001   9.82978047680002E-0003

   2.00001000000000E+0001   9.83067834079003E-0003

   2.00010000000000E+0001   9.83876261538675E-0003

   2.00011000000000E+0001   9.83966125697929E-0003

Даже если увеличить возмущение более высоких степеней, взяв в частности возмущение при x¹⁶ равным 10⁶,

func:=abs(p*p1*p0+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+

1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+

1e-22*((sqr(sqr(sqr(x))))*x*x*x +1e-20*(sqr(sqr(sqr(x))))*x*x+1e-18*(sqr(sqr(sqr(x))))*x+

1e+6*(sqr(sqr(sqr(x))))+1e+2*((sqr(sqr(x))))*x*x*x-1e+8*((sqr(sqr(x))))*x*x-1e+4*((sqr(sqr(x))))*x+

1*sqr(sqr(x))+1.4*sqr(x)*x+1.8*sqr(x)+2.2*x+2.6);

то это все равно повлечет правильные значения корней:

  -2.00001000000000E+0001   3.27902073375188E-0003

  -2.00000000000000E+0001   3.27869951040001E-0003

  -2.00000000000000E+0001   3.27869951040001E-0003

  -2.00001000000000E+0001   3.27902073375188E-0003

  -1.99990000000000E+0001   3.27548891305416E-0003

  -1.99991000000000E+0001   3.27580983895904E-0003

  -1.90010000000000E+0001   1.19920023578432E-0003

  -1.90011000000000E+0001   1.19932435943367E-0003

  -1.90001000000000E+0001   1.19808366918073E-0003

  -1.90000000000000E+0001   1.19795966689766E-0003

……………………………………………………………..

  -2.00000000000000E+0000  -6.14369429254048E-0013

  -2.00010000000000E+0000  -6.14551203980037E-0013

  -1.99910000000000E+0000  -6.12735454352656E-0013

  -1.99900000000000E+0000  -6.12554123388815E-0013

  -2.00110000000000E+0000  -6.16371395916785E-0013

  -2.00100000000000E+0000  -6.16189176576129E-0013

  -1.00000000000000E+0000  -9.89900991909100E-0015

  -1.00010000000000E+0000  -9.90493089828411E-0015

  -1.00100000000000E+0000  -9.95835237480499E-0015

  -1.00110000000000E+0000  -9.96430285625631E-0015

   ……………………………………………………………

   1.90010000000000E+0001   3.86111320337299E-0003

   1.90011000000000E+0001   3.86148342762584E-0003

   1.90000000000000E+0001   3.85741281096815E-0003

   1.90001000000000E+0001   3.85778269887821E-0003

   1.99990000000000E+0001   9.82336509971562E-0003

   1.99991000000000E+0001   9.82426228910537E-0003

   2.00000000000000E+0001   9.83234048960002E-0003

   2.00001000000000E+0001   9.83323845599227E-0003

   2.00010000000000E+0001   9.84132365237045E-0003

   2.00011000000000E+0001   9.84222239640108E-0003

Следует заметить, что в последнем варианте программы был заблокирован оператор //if abs(aaa-x)<=1e-20 then goto 22; чтобы избежать возможного пропуска корней.

Можно заключить, что вопрос об устойчивости вычисления корней полинома в зависимости от возмущения коэффициентов остается далеко не закрытым. Ответ на него требует более глубокого исследования, чем только лишь численный эксперимент.

Конкретно представленные результаты эксперимента существенно уточняют результаты, приведенные в [10].

Заключение. Компьютерный метод идентификации корней полиномов на основе сортировки используется для исследования зависимости корней от возмущения коэффициентов полинома. С помощью численного эксперимента показано, что метод идентифицирует все (в том числе плохо отделенные) вещественные корни полиномов степени 240 с верными знаками мантисс в формате данных extended. При этом, как альтернатива известному примеру Уилкинсона, правильная работа метода сохраняется при возмущении коэффициентов полинома на значительную величину.