Продольные упруго-вязкопластические волны напряжений в геометрически неоднородных стержнях

Ударное нагружение стержневых конструкций из деформируемых материалов в процессе их эксплуатации сопровождается распространением в материале различных типов волн напряжений, качественные характеристики и количественные параметры которых определяются тремя группами факторов: 1) механическими свойствами и характеристиками материала; 2) особенностями геометрическими особенностями конструкции стержня; 3) характером и количественными параметрами внешней нагрузки. При этом следствием процессов распространения и интерференции волн напряжений в материале может стать его единичная или множественная откольная деструкция трансформация волны в процессе ее распространения из упругой в вязкопластическую, а также откольная деструкция материала, что в подавляющем числе случаев реальной эксплуатации является недопустимым. Поэтому умение прогнозировать последствия ударного нагружения и определять параметры напряженно-деформированного и кинематического состояний материала – важная и актуальная научно-техническая задача [1, 2]. Ниже предпринята попытка физического и математического моделирования этой ситуации.

Рассматривается прямолинейный стержень конечной длины L, свойства материала которого описываются конституционными уравнениями Малверна-Соколовского-Кристеску вида [2]

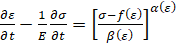,     (1)

где 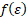 – диаграмма квазистатического нагружения материала; 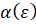,  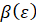– аппроксимирующие функции, характеризующие его вязко-пластические свойства; E – модуль упругости материала.

В момент времени t = 0 к торцу стержня прикладывается разрывной импульс растягивающих напряжений вида [3]:

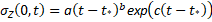,      (2)

где a, b, c, t* – константы, определяемые обработкой экспериментальных кривых изменения давления методом наименьших квадратов.

Граничные условия задачи соответствуют первоначально ненапряженному, недеформированному и неподвижному материалу стержня:

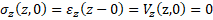,    (3)

где z – лагранжева координата, совпадающая с продольной осью стержня с началом в точке приложения внешнего импульса давления.

Стержень имеет круговое поперечное сечение, образующая которого описывается заданной непрерывной негладкой функцией y = y(z).

Полная система уравнений, описывающая распространение продольной волны растягивающих или сжимающих напряжений в стержне в самом общем случае, соответствующем упруго-вязкопластической модели материала и геометрической неоднородности стержня, включает в себя уравнения движения материала, уравнение совместности деформаций (или уравнение неразрывности) и конституционное уравнение (1) и является квазилинейной:

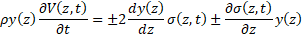
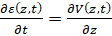,     (4)

,                                                                       

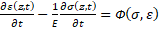где 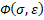 – условное обозначение правой части конституционного уравнения (1), знак (+) в правой части уравнения движения соответствует волне растягивающих напряжений, знак (-) – случаю напряжений сжатия. В дальнейшем в рамках данной статьи будет анализироваться первый случай.

Если положить в (4) материал стержня линейно упругим, то есть обнулить правую часть уравнения (1) и, соответственно, – последнего уравнения системы (4), и рассматривать стержень геометрически однородным, то есть считать y(z)= const, то система уравнений (4) вырождается в классическую линейную систему волновых уравнений, имеющую аналитическое решение в форме Даламбера [1, 2]. При этом изменение каждого параметра напряженно-деформированного и кинематического состояний материала стержня во времени в различных поперечных сечениях будут описываться функциями, не зависящими от лагранжевой координаты z.

Рассмотрим теперь менее частный по отношению к предыдущему вариант формулировки волновой задачи, имеющий важное практическое приложение: пусть параметры начальных условий и геометрия нагружаемого торца стержня таковы, что на нагружаемом торце формируется волна упругих напряжений, которая распространяется в геометрически неоднородный стержень. При этом упругое состояние материала ограничено сверху, то есть существуют некоторое предельное напряжение или, в общем случае, некоторое формализованное условие, при превышении или невыполнении которых материал переходит в упруго-вязкопластическое состояние, соответствующее конституционному уравнению (1), а при невыполнении дополнительных условий – разрушается. Наиболее приемлемые и апробированные для широкой группы металлов варианты записи уравнений предельного состояния получены в работе [2].

В этом случае общая система уравнений (4) принимает вновь квазилинейный вид:

,                                      

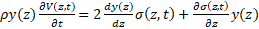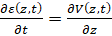,        (5)

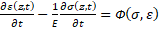
но в процессе ее решения необходимо непрерывно, на каждом шаге численного интегрирования, отслеживать изменение значений напряжений и деформаций в материале и производить сравнение их с критерием предельного состояния, соответствующим выходу материала из зоны упругости. И физической причиной этого перехода в такой постановке задачи будет являться геометрическая неоднородность стержня, что отражает первое слагаемое в правой части уравнения движения. Такая постановка волновой задачи, как показал проведенный анализ, является новой.

Следуя [4], определим, к какому типу дифференциальных уравнений в частных производных относится система (5). Для этого дополним ее тремя соотношениями для полных дифференциалов искомых функций 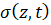, , 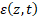, 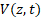в результате чего получим систему шести уравнений, которая по отношению к шести первым частным производным искомых функций будет являться линейной алгебраической. Потребуем ее неопределенности, которая впоследствии позволит найти искомые решения, удовлетворяющие начальному и граничным условиям. Неопределенность линейной алгебраической системы уравнений реализуется, когда ее главный и любой неглавный определители тождественно равны нулю.

Равенство нулю главного определителя системы позволяет получить в дифференциальной форме уравнения характеристических направлений системы (5) в плоскости независимых переменных z – t:

,

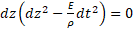Откуда

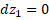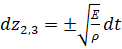, ,    (6)

где 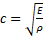– скорость распространения продольной волны упругих напряжений в материале стержня.

Таким образом, система уравнений (5) имеет три действительные характеристики, то есть по-прежнему, как и классическая система волновых уравнений, упоминавшаяся выше, является системой гиперболического типа. Таким образом, геометрическая неоднородность стержня не влияет на тип соответствующей ей системы уравнений, что является, как будет показано в дальнейшем, важным практическим обстоятельством.

Приравнивая любой из шести неглавных определителей системы нулю и подставляя последовательно в полученное уравнение дифференциальные уравнения характеристик (6), получаем рабочие уравнения, устанавливающие связь между полными дифференциалами искомых функций вдоль соответствующих характеристических направлений:

– вдоль характеристического направления dz=0:

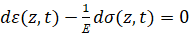,     (7)

– вдоль характеристических направлений :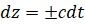

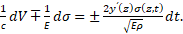  (8)

Теперь интегрирование квазилинейной гиперболической системы дифференциальных уравнений в частных производных (5) можно заменить с точностью до линейного преобразования интегрированием системы обыкновенных дифференциальных уравнений (7)-(8), записанных вдоль прямолинейных характеристических направлений (6). Причем для последней системы с помощью начальных (2) и граничных (3) условий сформулирована краевая задача Гурса [4]. Для численного решения последней разработан программный комплекс Plarit [5].

В случае выхода параметров волны в процессе распространения по стержню за пределы упругого состояния материала системы уравнений (5) и (7)-(8) видоизменяются, так как в правой части конституционного уравнения появляется функция 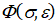, описывающая вязкопластические свойства материала. Комплекс [5] позволяет решать и эту задачу. При этом возможны качественно различные исходы волнового нагружения стержня:

• в случае хрупкого характера разрушения материала, что с учетом его скоростного охрупчивания в волне наиболее вероятно, разрушение материала происходит вследствие уменьшения поперечных габаритов стержня и, как следствие – увеличения амплитудных значений параметров напряженно-деформированного состояния, в зоне упругого состояния материала;
• если параметры напряженно-деформированного состояния материала изменяются на участке упругого состояния таким образом, что не выводят его за пределы критерия разрушения, и упругая волна трансформируется в упруго-вязкопластическую, то разрушение материала возможно в зоне его неупругого волнового деформирования.

Таким образом, в данной работе сформулирована и доведена до уровня возможности ее практической реализации актуальная задача оценки в том числе и деструктивных последствий волнового нагружения стержней из упругих и упруго-вязкопластических материалов с геометрической неоднородностью.