О компьютеризации анализа устойчивости дифференциальных систем

Постановка вопроса. Известные методы качественной теории дифференциальных уравнений [1, 2] разработаны в теоретическом аспекте, тем не менее, они лежат в основе практически всех применений [3, 4]. На данный момент использование средств вычислительной техники для анализа устойчивости не является предметом системного исследования, хотя связь численных методов с устойчивостью изучается с применением компьютеров [5-7]. Непосредственное использование численных методов решения обыкновенных дифференциальных уравнений (ОДУ) для построения критериев устойчивости предпринято в [8, 9], кроме того в [10, 11], а также в [12, 13]. На этой основе удается сформулировать необходимые и достаточные условия устойчивости конструктивного характера, которые реализуемы программно и дают возможность численного моделирования устойчивости по ходу решения ОДУ. В предлагаемом сообщении с помощью численного и программного эксперимента исследуется соответствие практике численного моделирования критериев устойчивости, полученных на основе связи с численными методами. Описание результатов включает коды программ и распечатки результатов их работы для нелинейных и линейных систем.

Исходные условия и предположения. Пусть рассматривается задача Коши для системы ОДУ, которая имеет нулевое решение (точку покоя) ,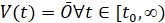

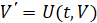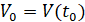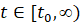,        ,        ,    (1)

где 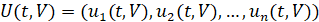, , 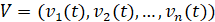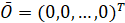. Исследуется устойчивость в смысле Ляпунова точки покоя этой системы. Ниже возмущение 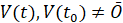, нулевого решения не будет отмечаться специальным символом. Используются канонические нормы вектора, по умолчанию 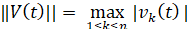. Предполагается, что существует 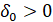, такое что в области 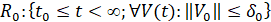, , 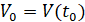выполнены все условия существования и единственности решения, в частности, вектор-функция  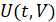определена, непрерывна в R₀ и удовлетворяет условию Липшица: 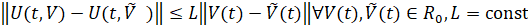. Для дальнейшего потребуется ограничение, из которого следует условие Липшица. Именно, ниже предполагается, что выполнено соотношение:

uk(t,V)-uk(t,V)≤Lvk(t)-vk(t),L=const∀t∈[t0,∞),∀V(t),V(t)∈R0,∀k∈1,n

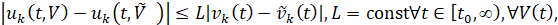
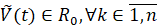.      (2)

В случае, когда сравниваются нулевое решение и его возмущение, с учетом 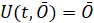 условие Липшица примет вид 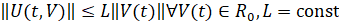, а соотношение (2) перейдет в соотношение

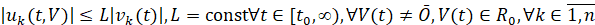 .     (3)

В рассматриваемых условиях точка покоя устойчива, если 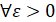 найдется 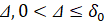, такое что  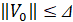влечет 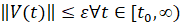. Точка покоя асимптотически устойчива, если она устойчива и найдется 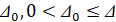, такое что из неравенства  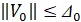следует .

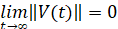Необходимые и достаточные условия устойчивости точки покоя. В рассматриваемых предположениях, в частности включающих (2), (3), в [10, 11], а также в [12, 13] предложены следующие критерии устойчивости и асимптотической устойчивости.

Теорема 1. Для устойчивости точки покоя системы (1) необходимо и достаточно существование 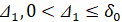, такого, что  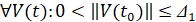выполняется соотношение

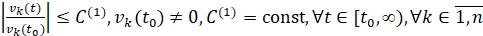. (4)

Для асимптотической устойчивости необходимо и достаточно, чтобы решение было устойчиво и существовало 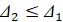, такое, что  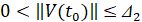влечет

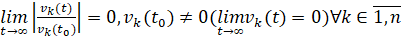.     (5)

Достаточные условия (4), (5) имеют место в более широком случае лишь единственности решения.

Теорема 2. В рассматриваемых условиях, включая ограничения (2), (3), для устойчивости точки покоя системы (1) необходимо и достаточно существование 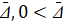, такого что  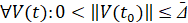выполняется соотношение

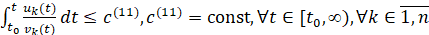.    (6)

Для асимптотической устойчивости необходимо и достаточно, чтобы решение было устойчиво и существовало 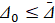, такое что  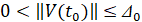влечет

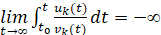
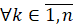    .    (7)

Обращение в ноль знаменателя подынтегральной функции при условии (3) приводит лишь к устранимым особенностям [12], что не влечет некорректности интегрирования. В [11] показано, что теоремы 1, 2 вытекают из мультипликативных преобразований метода Эйлера

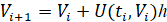.    (8)

На произвольном отрезке 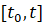 метод (8) рассматривается в предположении, что значение независимой переменной  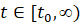является произвольно фиксированным, при этом индекс i неограниченно растет одновременно с убыванием равномерного шага:

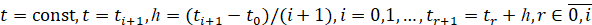.     (9)

Следствие 1. Теорема 2 сохраняется, если соотношения (6), (7) заменить соответственно на соотношения вида:

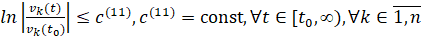.      (10)

и

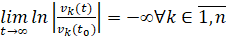.    (11)

где .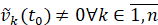

Для линейных систем ОДУ не требуется проверять рассматриваемые соотношения теорем 1 и 2 в Δ – окрестности нулевого начального вектора – достаточно проверить их выполнение для любого отдельно взятого решения, соответствующего начальному вектору со всеми ненулевыми компонентами [12]. Для линейных систем можно применять условия устойчивости, которые полностью не зависят от начальных значений [8, 9]. Пусть рассматривается однородная система

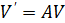    (12)

с матрицей вещественных коэффициентов n×n. Имеет место

Теорема 3 [10, 11]. Система (12) устойчива тогда и только тогда, когда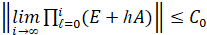, , 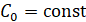, 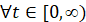для асимптотической устойчивости необходимо и достаточно, чтобы 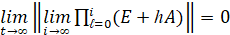, где h из (9), E – единичная матрица.

Вычисление степени 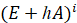 заменяется вычислением :

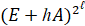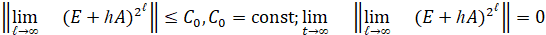     (13)

При достаточно малом h реализация (13) сводится к умножению матрицы 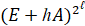 на себя до момента достижения заданной границы изменения t.

Численное моделирование устойчивости. Пусть рассматривается система

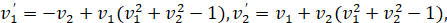       (14)

где 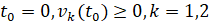, и требуется исследовать на устойчивость ее точку покоя. Запрограммировано (Delphi) решение задачи (14) методом Эйлера на отрезке [0,10000] с шагом h=10^-4. На выходе программы формируются компоненты левых частей (4). Выводится эвклидова норма (norma (V/V0)) от обоих компонентов 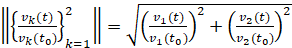. Выводятся также значения интегралов (INTEGRAL(v1/v10), INTEGRAL(v2/v20)) компонентов левой части (6), выраженные через первообразные согласно (10), (11).

program NORMALOGVnew11;
{$APPTYPE CONSOLE}
uses
  SysUtils;

const  h = 0.0001;  tt=10000000;
var t,t0,v1,v2,v10, v20,u10, u20: extended; k: longint;
function u1(t,v1,v2:extended):extended;
begin u1:=-v2+v1*(sqr(v1)+sqr(v2)-1); end;
function u2(t,v1,v2:extended):extended;
begin u2:=v1+v2*(sqr(v1)+sqr(v2)-1); end;

begin
k := 0; t0:=0.0; v10:=-0.005*0.005; v20:=0.005*0.005;
v1:=v10; v2:=v20; t:=t0; while t <=10000 do
begin
v1:= v1+ h * u1(t,v1,v2); v2:= v2+ h * u2(t,v1 ,v2 );
k:=k+1;   if k =  tt then
begin
writeln ('t=',t:4,' ');
writeln ('norma (V/V0)=',sqrt(sqr(v1/v10)+sqr(v2/v20)):4);
writeln ('INTEGRAL(v1/v10)=',ln(abs(v1/v10)):4);
writeln ('INTEGRAL(v2/v20)=',ln(abs(v2/v20)):4);
writeln;
k:=0 end; t:=t+h; end;
readln
end.
Результат работы программы:
t= 1.0E+0003
norma (V/V0)= 6.8E-0435
INTEGRAL(v1/v10)=-1.0E+0003
INTEGRAL(v2/v20)=-1.0E+0003

t= 2.0E+0003
norma (V/V0)= 3.3E-0869
INTEGRAL(v1/v10)=-2.0E+0003
INTEGRAL(v2/v20)=-2.0E+0003

t= 3.0E+0003
norma (V/V0)= 1.6E-1303
INTEGRAL(v1/v10)=-3.0E+0003
INTEGRAL(v2/v20)=-3.0E+0003

t= 4.0E+0003
norma (V/V0)= 7.7E-1738
INTEGRAL(v1/v10)=-4.0E+0003
INTEGRAL(v2/v20)=-4.0E+0003

t= 5.0E+0003
norma (V/V0)= 3.7E-2172
INTEGRAL(v1/v10)=-5.0E+0003
INTEGRAL(v2/v20)=-5.0E+0003

t= 6.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-6.0E+0003
INTEGRAL(v2/v20)=-6.0E+0003

t= 7.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-7.0E+0003
INTEGRAL(v2/v20)=-7.0E+0003

t= 8.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-8.0E+0003
INTEGRAL(v2/v20)=-8.0E+0003

t= 9.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-9.0E+0003
INTEGRAL(v2/v20)=-9.0E+0003

t= 1.0E+0004
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-1.0E+0004
INTEGRAL(v2/v20)=-1.0E+0004

Из распечатки видно, что эвклидова норма 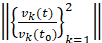 убывает к нулю на отрезке [0,10000] и одновременно интегралы убывают к -∞. Полученные результаты указывают на признаки асимптотической устойчивости согласно (4), (5), а также согласно (6), (7). Аналогичного вида признаки воспроизводятся в ненулевых точках любой не большей по диаметру окрестности (t0:=0; v10:=-0.005*0.005; v20:=0.005*0.005;) нулевого начального вектора. Вывод относительно асимптотической устойчивости точки покоя системы (14) согласуется с результатом ее аналитического исследования, изложенного в [14]. Если теперь в правой части этой системы ввести числовые коэффициенты

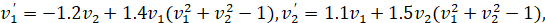
то по той же программе с модификацией подпрограмм, задающих правые части,

function u1(t,v1,v2:extended):extended;
begin u1:=-1.2* v2+1.4*v1*(sqr(v1)+sqr(v2)-1); end;
function u2(t,v1,v2:extended):extended;
begin u2:= 1.1*v1+1.5*v2*(sqr(v1)+sqr(v2)-1); end;

результат компьютерного анализа сохранится с некоторым изменением численных значений:

t= 1.0E+0003
norma (V/V0)= 2.5E-0630
INTEGRAL(v1/v10)=-1.4E+0003
INTEGRAL(v2/v20)=-1.5E+0003

t= 2.0E+0003
norma (V/V0)= 4.0E-1260
INTEGRAL(v1/v10)=-2.9E+0003
INTEGRAL(v2/v20)=-2.9E+0003

t= 3.0E+0003
norma (V/V0)= 7.0E-1890
INTEGRAL(v1/v10)=-4.3E+0003
INTEGRAL(v2/v20)=-4.4E+0003

t= 4.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-5.8E+0003
INTEGRAL(v2/v20)=-5.8E+0003

t= 5.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-7.3E+0003
INTEGRAL(v2/v20)=-7.3E+0003

t= 6.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-8.7E+0003
INTEGRAL(v2/v20)=-8.7E+0003

t= 7.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-1.0E+0004
INTEGRAL(v2/v20)=-1.0E+0004

t= 8.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-1.1E+0004
INTEGRAL(v2/v20)=-1.1E+0004

t= 9.0E+0003
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-1.1E+0004
INTEGRAL(v2/v20)=-1.1E+0004

t= 1.0E+0004
norma (V/V0)= 0.0E+0000
INTEGRAL(v1/v10)=-1.1E+0004
INTEGRAL(v2/v20)=-1.1E+0004

Если изменить коэффициенты следующим образом

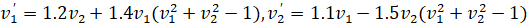,       (15)

соответственно внести их в описание подпрограмм,

function u1(t,v1,v2:extended):extended;
begin u1:=1.7* v2+1.7*v1*(sqr(v1)+sqr(v2)-1); end;
function u2(t,v1,v2:extended):extended;
begin u2:= 1.1*v1+1.1*v2*(sqr(v1)+sqr(v2)-1); end;

то результат работы программы укажет на устойчивость (но не асимптотическую) точки покоя системы (15):

t= 1.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 2.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 3.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 4.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 5.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 6.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 7.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 8.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 9.0E+0003
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

t= 1.0E+0004
norma (V/V0)= 3.0E-0001
INTEGRAL(v1/v10)=-1.5E+0000
INTEGRAL(v2/v20)=-1.5E+0000

Легко подобрать коэффициенты, чтобы точка покоя оказалась неустойчивой. В этом случае либо происходит переполнение, либо рост эвклидовой нормы и интегралов в запрограммированной форме.

Метод универсально (с точностью до размерности) подходит для анализа любых нелинейных и линейных систем. Однако в случае линейной системы с постоянными коэффициентами более наглядно работает критерий (13). Пусть, например, рассматривается система (12) с матрицей вида

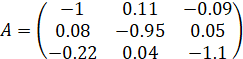.     (16)

Следующая программа реализует критерий (13) и выполнит анализ устойчивости системы с такой матрицей:

Program USTlinconstDU2222;
{$APPTYPE CONSOLE} uses
  SysUtils;

const n=3; h=1.1e-14;
type matr=array[1..n,1..n] of extended; vect=array[1..n] of extended;
const A: matr=   ((  -1, 0.11, -0.09),
                           ( 0.08,  -0.95,0.05),
                           (-0.22, 0.04, -1.1));
var   a1,c: matr; s0,s1,x: extended; i,j,l,k: integer;
procedure ummatr (var a1,c: matr);
var  s1: extended; i,j,l : integer;
begin  for i := 1  to  n do for j := 1  to  n do
begin s1:=0; for l:= 1 to n do s1:= s1+a1[i,l]*a1[l,j]; c[i,j]:= s1
end; end;
begin  for  i:=1 to n do for j:=1 to n do
begin a1[i,j]:=a[i,j]*h; if i=j then a1[i,j]:=a1[i,j]+1 end;
k:=0;  while  abs(x) <= 1.1e9 do begin
ummatr (a1,c); k:=k+1; x:=h*exp((k+1)*ln(2));
for i:=1 to n do for j:=1 to n do
a1[i,j]:=c[i,j]; s0:=0; for i:=1 to n do for j:=1 to n do
s0:=s0+sqr(a1[i,j]); s0:= sqrt(s0);  write ('  ':2, s0:2,'  ':8); end;
writeln; writeln; writeln ('  ':2, 'h =',h,'  ');
writeln ('  ':2, 'k=',k,'  ');writeln ('  ':2, 'x=',x:2,'  ');
readln
end. 

Результат работы программы:

1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.6E+0000	1.6E+0000	1.4E+0000	1.2E+0000
8.0E-0001	3.8E-0001	9.1E-0002	5.7E-0003	2.6E-0005
5.6E-0010	2.5E-0019	4.7E-0038	1.6E-0075	1.8E-0150
2.4E-0300
4.2E-0600	1.3E-1199	1.2E-2398	0.0E+0000	0.0E+0000
0.0E+0000	0.0E+0000
0.0E+0000	0.0E+0000	0.0E+0000	0.0E+0000	0.0E+0000
0.0E+0000	0.0E+0000
0.0E+0000	0.0E+0000	0.0E+0000	0.0E+0000	0.0E+0000
0.0E+0000

h = 1.10000000000000E-0014

k=76

x= 1.7E+0009

На отрезке abs(x) <= 1.1e9 программа эквивалентно методу Эйлера с шагом h = 1.1E-0014 умножает матрицу E+hA на себя k=76 раз. Эвклидова норма текущей степени убывает до нуля, что согласно теореме 3 означает асимптотическую устойчивость. Это так, поскольку матрица имеет диагональное преобладание отрицательных элементов. Для матрицы 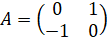, соответственной системе 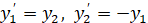, получится устойчивость (но не асимптотическая):

1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000	1.4E+0000
1.5E+0000

h = 1.10000000000000E-0014

k=76

x= 1.7E+0009

Если изменить знак элементов на диагонали матрицы (16) на противоположный, то получится неустойчивость:

1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000
1.7E+0000	1.7E+0000	1.7E+0000	1.7E+0000	1.8E+0000
1.8E+0000	1.8E+0000	1.9E+0000	2.1E+0000	2.6E+0000
3.9E+0000	8.9E+0000	5.1E+0001	1.9E+0003	3.2E+0006
8.8E+0012	6.4E+0025	3.4E+0051	9.6E+0102	7.6E+0205
4.8E+0411

h = 1.10000000000000E-0014

k=56

x= 1.6E+0003

Отрезок пришлось, как обычно в таких случаях, сократить до abs(x) <= 1.1e3, иначе наступает переполнение.

Заключение. В работе представлены критерии устойчивости по Ляпунову, которые дают возможность численного моделирования устойчивости по ходу решения задачи Коши для ОДУ. Показана конструктивность критериев, выполнены численные эксперименты, подтверждающие их достоверность, детализированы способы программной реализации.