Development of a method to ensure the reliability and confidentiality of data based on code-theoretical schemes with elliptical curves in telecommunications networks

1. Introduction

The Cryptography could be a method which provides security to data. In cryptography all the information is presented within the scrambled frame and as it were authorized user can unscramble information. The most goals of cryptography are to preserve information confidentiality, integrity, availability, centralized information collection to provide information realness within the advanced world that provide tall security to database. Plaintext could be a term used in cryptography that alludes to a message before encryption or after decoding. That's, it could be a dispatch in a shape that's effortlessly clear by people. Cipher text is moreover known as scrambled or encoded information since it contains a shape of the special plaintext that is unreadable by a human or computer without the proper cipher to decode it. A cryptographic key is a string of bits utilized by a cryptographic calculation to transform plain content into cipher content or bad habit versa.

In cryptography Elliptic Curve Cryptography (ECC) is one of the successful cryptography algorithm which was found in 1985 by Neil Koblitz and Victor Mill operator. Elliptic Curve Cryptographic (ECC) are Public-key instruments that give the same functionality as Rivest-Shamir-Adlemon algorithm. Most of the measures that utilize public-key cryptography for encryption based on RSA algorithm. Their security is based on the hardness of a distinctive. Their safety is contingent on the difficulty of several issues. The competing calculation to RSA is elliptic curve cryptography over limited areas.

2. Related Work

In final twenty a long time, elliptic curve cryptography has been completely investigated. The genuine application of elliptic curve cryptography and the down to earth execution of cryptosystem primitives within the genuine world constitute interdisciplinary constitute interdisciplinary investigate in computer science as well as in electrical building. Elliptic curve cryptography has evolved into a cutting-edge technique that is being utilized by a growing number of businesses. There are two reasons for this modern advancement.

The first is that ECC has survived an era of attacks.

The second within the developing businesses, its points of interest over RSA have made it an appealing security alternative.

Elliptic curve cryptography isn't as it were risen as an attractive open key cryptosystem for portable or wireless situations but moreover gives bandwidth savings. ECC encompasses a tall level of security which can be achieved with tall impressively shorter keys than other customary open key cryptography. ECC has an advantage that it makes a difference to set up equivalent security with lower calculating control and battery resource utilization for versatile applications. The quality of encryption depends on its key and the alphabetical table. As much as the key measure is influencing the execution time, it ought to be protected to be as brief as conceivable for a worthy security prerequisite.

There will be no affect on quality and runtime execution. ECC provides a great arrangement of information and secure transfer of keys between two communicating parties. An elliptic curve cryptography based communication framework, where the different characters can be symbolized as the co-ordinates of the elliptic curves, can too be produced. ECC structure is a group structure based on non-singular curve having finite number of numbers focuses with each of this point having a limited arrange. A novel thought of ECC encryption and unscrambling based on Rucksack too appears on how the elliptic curves innovation can be utilized for encryption and unscrambling.

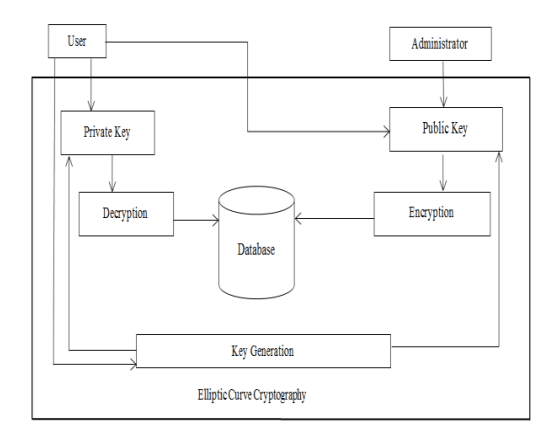
Fig. 1. System architecture

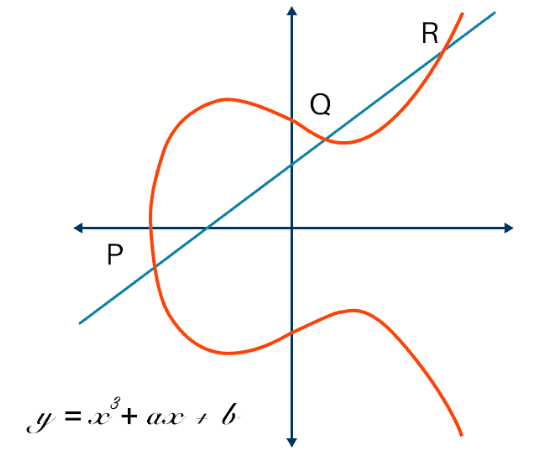
Fig. 2. Elliptic Curve

3. Proposed System

A common Elliptic Curve condition takes the general form:

y² = x³+ ax + b    (1)

 (x, y) = coordinates on the Elliptic curve

a, b = coefficients

In spite of the fact that, for settled areas a progressed condition is used:

y² mod q = (x³ +ax + b) mod q     (2)

Where q = prime number for which the Elliptic curve be characterized a, b fulfill the condition

(4a³ + 27b³) mod q ≠ 0 mod q    (3)

An elliptic curve E over GF (q) comprise of the answers (x, y) unmistakable by (1) and (2), at the side a supplementary component called 0, which is the point of EC at unendingness. The set of focuses (x, y) are said to be affine synchronize point exhibit. Calculation and replication are the two most basic operations on elliptic curves. A scalar propagation with a point can be denoted as a combination of calculation operations.

Let's say you have a point P (x, y) that needs to be multiplied k times,

say k = 37.

Hence we got to compute 37P.

In terms of expansion it can be spoken to as 37P = P + P + P +… + P (37 times) For expansion of two focuses P(x1, y1) & Q(x2, y2) where P≠Q.

3.1. System Architecture

Fig. 1 appears the design of the framework. System architecture depicts the different modules display in paper which are interrelated to each other. The previously executed a few calculation like RSA, Diffie Hellman has disadvantages which might moderate down the key era and encryption handle.

So elliptic curve cryptography calculation is successful to increase the speed of key era and encryption process. Encryption is done by the director by using public key of client. At that point decoding takes put by user by utilizing private key.

As each client has its separate private key so no other client can get to the information. If Chairman and client need to scramble and decrypt the messages at that point they concur upon to utilize an elliptic curve Ep (a, b) where p could be a prime number and the elliptic curve's random point C.

Client chooses a random number and a point A on the elliptic curve. User computes A1 = a (C +A) and A2 = a A. Client keeps the irregular number a and the point A as her private keys and conveys A1 and A 2 as her common public keys.

Following keys are required for ECC:

Step 1.

User’s private key 1 = a, a irregular number less than the arrange of the generator

Step 2.

2 = a point A on the elliptic curve Ep of the user's private key (a, b).

Step 3. 1 = a point A1 on the elliptic curve Ep for the user's global public key (a, b).

Step 4. 2 = a point A2 on the elliptic curve Ep of the user's general public key (a, b)

Step 5. User’s particular open key for chairman = a point AB on the elliptic curve Ep (a, b).

On the off chance that chairman needs to scramble the message M then all the characters of the expedite are coded to the focuses on the elliptic curve utilizing the code table which is concurred upon by the director and student. At that point each message point is scrambled to a pair of cipher focuses E1, E2.

Administrator uses a random number r.

E1 = r C E2 = M + (b + r) A 1 – r A 2 + AB

After scrambling all the characters of the message administrator changes over the match of focuses of each message point into the content characters utilizing the code table. At that point chairman scrambles the plain text.

After scrambling the cipher content, User converts the cipher content into the focuses on the elliptic curve and distinguishes the focuses E1 and E2 of each character. At that point unscrambles the message as follows.

M = E2 – (a E1 + a B 1 + B A)

Thus, Client can see this unscrambled information as he needs.

3.2. Algorithm of ECC

1. Start

2. Client perform the registration

3. Client enter private key1 and private key2(x, y).

4. Client calculate the public key, Calculates s s=(3(x)^2+a)/2y x2=s^2-2x y2=s(x-x2)-y

5. Client broadcast public key (X2, Y2)

6. Admin performs encryption

6.1. For each character, calculate 1G to 5G.

6.2. Recover coordinated G from generated table

6.3. Calculate G of that character which admin needs to scramble and store cipher text.

7. Client performs decryption

7.1. For each character, calculate 1G to 5G.

7.2. Recover coordinated G from generated table and stores the plain text.

8. Stop.

Result

RSA key era is expressively slower than ECC key era for RSA key of sizes 1024 bits which is greater than key measure of ECC. RSA has more computational overheads than ECC since in RSA algorithm, clients got to select specific prime number for calculation of key era. As the key size of ECC is littler than the key measure of RSA so, encryption of Elliptic curve cryptography is much faster than RSA. ECC is more effective for small devices. In case ECC calculation is utilized for communication purpose at that point it offers great transfer speed than RSA.

Table 1

Comparison of ECC and RSA

5. Conclusion

In this paper, Information security is vital issue in day to day life. The elliptic curve cryptography is one of the valuable methods to stow away the information or information so that information must be get to by authorized client. In this technique all the calculations are takes put by considering the focuses on the elliptic curve. The encryption and key era handle are speedier.

Remote gadgets are quickly getting to be more reliant on security highlights such as the capacity to do secure email, certain Web browsing, and cybernetic private organizing to commercial systems and ECC allows more productive usage of all of these features. ECC make accessible superior security and more effective execution than the primary generation public key procedures.